Calculateur de valeur p

Bienvenue sur notre calculateur de valeur p ! Vous n'aurez plus jamais à vous poser la question de savoir comment trouver la valeur p, puisque vous avez la possibilité de calculer les valeurs p unilatérales et bilatérales pour les statistiques de test, en suivant toutes les lois les plus courantes : normale, t de Student, khi-deux et F de Snedecor.

Les valeurs p sont omniprésentes en sciences, mais beaucoup trouvent le concept un peu intimidant. Ne vous inquiétez pas, car dans cet article, nous vous expliquerons non seulement ce qu'est la valeur p, mais aussi comment interpréter correctement les valeurs p. Vous êtes-vous déjà demandé·e comment calculer la valeur p à la main ? Nous vous fournissons également toutes les formules dont vous aurez besoin !

Formellement, la valeur p est la probabilité que la statistique de test produise des valeurs au moins aussi extrêmes que la valeur qu'elle a produite pour votre échantillon. Il est essentiel de se rappeler que cette probabilité est calculée en supposant que l'hypothèse nulle H₀ est vraie !

Plus intuitivement, la valeur p répond à la question suivante :

En supposant que je vive dans un monde où l'hypothèse nulle est vraie, quelle sera la probabilité que, pour un autre échantillon, le test que j'effectue produise une valeur au moins aussi extrême que celle que j'ai observée pour l'échantillon dont je dispose déjà ?

C'est l'hypothèse alternative qui détermine ce que  « extrême » signifie réellement, ainsi la valeur p dépend de l'hypothèse alternative que vous énoncez : unilatérale à gauche, unilatérale à droite ou bilatérale. Dans les formules ci-dessous, S représente une statistique de test, x la valeur qu'elle produit pour un échantillon donné et P(événement | H₀) la probabilité d'un événement, calculée en supposant que H₀ est vraie :

1. Test unilatéral à gauche : valeur p = P(S ≤ x | H₀)

2. Test unilatéral à droite : valeur p = P(S ≥ x | H₀)

3. Test bilatéral :

   valeur p = 2 × min{P(S ≤ x | H₀), P(S ≥ x | H₀)}

   (Avec min{a,b}, nous désignons le plus petit nombre parmi a et b)

   Si la distribution de la statistique du test sous H₀ est symétrique autour de 0, alors :
   valeur p = 2 × P(S ≥ |x| | H₀)

   ou, de manière équivalente,
   valeur p = 2 × P(S ≤ -|x| | H₀)

Une image valant mille mots, illustrons ces définitions. Nous utilisons ici le fait que la probabilité peut être représentée de manière claire comme l'aire sous la courbe pour une loi de probabilité donnée. Nous avons deux séries d'images : l'une pour une distribution symétrique et l'autre pour une distribution asymétrique (non symétrique).

• Cas symétrique : loi normale

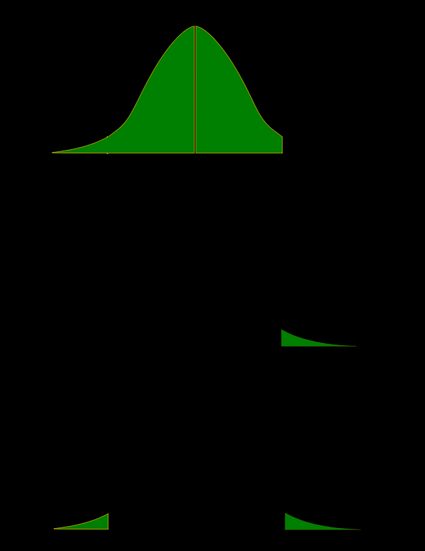
• Cas non symétrique : loi du khi-deux

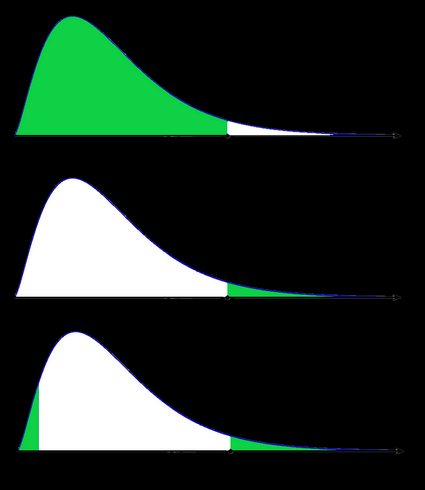
Dans la dernière image (la valeur p bilatérale pour une distribution asymétrique), l'aire du côté gauche est égale à l'aire du côté droit.

Pour déterminer la valeur p, vous avez besoin de connaître la loi de votre statistique de test en supposant que l'hypothèse nulle est vraie. Ensuite, à l'aide de la fonction de répartition (fdr), nous pouvons exprimer la probabilité que la statistique du test soit au moins aussi extrême que sa valeur x pour l'échantillon :

1. Test unilatéral à gauche :

   valeur p = fdr(x)

2. Test unilatéral à droite :

   valeur p = 1 - fdr(x)

3. Test bilatéral :

   valeur p = 2 × min{fdr(x) , 1 - fdr(x)}

   Si la distribution de la statistique du test sous H₀ est symétrique autour de 0, alors une valeur p bilatérale peut être simplifiée en valeur p = 2 × fdr(-|x|), ou, de manière équivalente, en valeur p = 2 - 2 × fdr(|x|).

Les lois de probabilité les plus répandues dans les tests d'hypothèses ont tendance à avoir des formules pour les fonction de répartition compliquées, et il n'est pas toujours possible de trouver la valeur p à la main. Vous devrez probablement avoir recours à un ordinateur ou à un tableau statistique, dans lequel les statisticiens ont rassemblé des valeurs approximatives de fonctions de répartition.

Vous savez maintenant comment calculer la valeur p, mais... pourquoi avez-vous besoin de calculer ce chiffre ? Dans les tests d'hypothèse, la valeur p est une alternative à l'approche de la valeur critique. Rappelons-nous que cette dernière exige des chercheurs qu'ils fixent à l'avance le seuil de signification, α, qui est la probabilité de rejeter l'hypothèse nulle lorsqu'elle est vraie (donc d'une erreur de type I). Une fois que vous avez votre valeur p, il vous suffit de la comparer à un α donné pour décider rapidement s'il faut ou non rejeter l'hypothèse nulle à ce seuil de signification, α . Pour plus de détails, consultez la section suivante, où nous expliquons comment interpréter les valeurs p.

Comme nous l'avons mentionné ci-dessus, la valeur p est la réponse à la question suivante :

En supposant que je vive dans un monde où l'hypothèse nulle se vérifie, quelle est la probabilité que, pour un autre échantillon, le test que j'effectue génère une valeur au moins aussi extrême que celle que j'ai observée pour l'échantillon dont je dispose déjà ?

Qu'est-ce que cela signifie pour vous ? Vous avez deux possibilités :

• une valeur p élevée signifie que vos données sont hautement compatibles avec l'hypothèse nulle ; et
• une valeur p faible constitue une preuve contre l'hypothèse nulle, car elle signifie que votre résultat serait très improbable si l'hypothèse nulle était vraie.

Cependant, il peut arriver que l'hypothèse nulle soit vraie, mais que votre échantillon soit très inhabituel ! Par exemple, imaginons que nous ayons étudié l'effet d'un nouveau médicament et que nous ayons obtenu une valeur p de 0,03. Cela signifie que dans 3% des études similaires, le hasard seul pourrait produire la valeur de la statistique de test que nous avons obtenue, ou une valeur encore plus extrême, même si le médicament n'avait aucun effet !

À la question « Qu'est-ce que la valeur p ? », on peut également répondre comme suit : la valeur-p est le plus petit seuil de signification auquel l'hypothèse nulle serait rejetée. Ainsi, si vous voulez maintenant prendre une décision sur l'hypothèse nulle à un certain seuil de signification α, il suffit de comparer votre valeur-p avec α :

• si la valeur p ≤ α, vous rejetez l'hypothèse nulle et acceptez l'hypothèse alternative ; et
• si valeur p ≥ α, vous n'avez pas assez de preuves pour rejeter l'hypothèse nulle.

Évidemment, le sort de l'hypothèse nulle dépend de α. Par exemple, si la valeur p était de 0,03, nous rejetterions l'hypothèse nulle à un seuil de signification de 0,05, mais pas à un seuil de 0,01. C'est pourquoi le seuil de signification doit être indiqué à l'avance et non pas adapté commodément après que la valeur p a été établie ! Un seuil de signification de 0,05 est la valeur la plus courante, mais elle n'a rien de magique. Il est toujours préférable d'indiquer la valeur p et de laisser le lecteur en tirer ses propres conclusions.

N'oubliez pas non plus que l'expertise dans le domaine (et un bon raisonnement scientifique) est crucial. Sinon, en appliquant sans réfléchir les principes statistiques, vous pouvez facilement arriver à statistiquement significatif, bien que la conclusion soit fausse à 100 %

Avec notre calculateur de valeur p à votre disposition, ne vous préoccupez plus de savoir comment obtenir la valeur p à partir de toutes ces statistiques de test complexes !
Voici ces étapes par lesquelles vous devez passer :

1. Choisissez l'hypothèse alternative : bilatérale, unilatérale à droite ou unilatérale à gauche.

2. Indiquez la loi de votre statistique de test sous l'hypothèse nulle : s'agit-il de N(0,1), t de Student, khi-deux ou F de Snedecor ? Si vous avez des doutes, référez-vous aux sections ci-dessous dédiées à ces lois.

3. Si nécessaire, précisez les degrés de liberté de la distribution de la statistique de test.

4. Saisissez la valeur de la statistique de test calculée pour votre échantillon de données.

5. Notre calculateur détermine la valeur p de la statistique de test et fournit la décision à prendre concernant l'hypothèse nulle. Le seuil de signification standard est de 0,05 par défaut.

Passez en Mode Avancé (Advanced mode) si vous souhaitez augmenter la précision avec laquelle les calculs sont effectués ou changer le seuil de signification.

En termes de fonction de répartition (fdr) de la loi normale standard, traditionnellement désignée par Φ, la valeur p est donnée par les formules suivantes :

1. Test Z unilatéral à gauche :

   valeur p = Φ(score Z)

2. Test Z unilatéral à droite :

   valeur p = 1 - Φ(score Z)

3. Test Z bilatéral :

   valeur p = 2 × Φ(-|score Z|)

   ou

   valeur p = 2 - 2 × Φ(|score Z|)

Nous utilisons le score Z si la statistique du test suit approximativement la loi normale centrée réduite N(0,1). Grâce au théorème central limite, vous pouvez compter sur cette approximation si vous disposez d'un grand échantillon (disons au moins 50 points de données) et que vous considérez votre loi comme étant normale.

Un test Z se réfère le plus souvent à un test de la moyenne de la population, ou à la différence entre deux moyennes de population, en particulier entre deux proportions. Vous pouvez également trouver des tests Z dans les estimations du maximum de probabilité.

La valeur p du score T (test de Student) est donnée par les formules suivantes, dans lesquelles fdr_t,d représente la fonction de répartition de la loi (cumulative) de Student avec d degrés de liberté :

1. Test de Student unilatéral gauche :

   valeur p = fdr_t,d(score T)

2. Test de Student unilatéral droit :

   valeur p = 1 - fdr_t,d(score T)

3. Test de Student bilatéral :

   valeur p = 2 × fdr_t,d(-|score T|)

   ou

   valeur p = 2 - 2 × fdr_t,d(|score T|)

Utilisez l'option score T si votre statistique de test suit la loi de Student. Cette loi est de forme similaire à N(0,1) (en forme de cloche et symétrique) mais avec des extrémités plus épaisses. La forme exacte dépend du paramètre appelé degrés de liberté. Si le nombre de degrés de liberté est élevé (> 30), ce qui est généralement le cas pour les grands échantillons, la loi de Student est pratiquement impossible à distinguer de la loi normale N(0,1).

Les tests de Student les plus courants sont ceux qui concernent les moyennes d'une population dont l'écart type est inconnu, ou la différence entre les moyennes de deux populations, dont les écarts types sont soit égaux, soit inégaux, mais inconnus. Il existe également un test de Student à échantillons appariés (dépendants).

Utilisez l'option score χ² lorsque vous effectuez un test dans lequel la statistique du test suit la loi du χ².

Cette loi apparaît si, par exemple, vous prenez la somme de variables élevées au carré, chacune suivant la loi normale N(0,1). N'oubliez pas de vérifier le nombre de degrés de liberté de la loi du χ² de votre statistique de test !

Découvrir la valeur p du khi-deux est une tâche simple ! Vous pouvez le faire grâce aux formules ci-dessous, où fdr_χ²,d représente la fonction de répartition de la loi du χ² avec d degrés de liberté :

1. Test du χ² unilatéral à gauche :

   valeur p = fdr_χ²,d(score χ²)

2. Test du χ² unilatéral à droite :

   valeur p = 1 - fdr_χ²,d(score χ²)

   N'oubliez pas que les tests du χ² d'ajustement et d'indépendance sont des tests unilatéraux ! (voir ci-dessous)

3. Test du χ² bilatéral :

   valeur p = 2 × min{fdr_χ²,d(score χ²), 1 - fdr_χ²,d(score χ²)}

   (Avec min{a,b}, nous désignons le plus petit des nombres a et b)

Voici les tests les plus courants qui conduisent à un score χ².

• Tester si la variance des données normalement distribuées a une certaine valeur prédéterminée. Dans ce cas, la statistique du test a une loi du χ² avec n - 1 degrés de liberté, où n est la taille d'échantillon. Il peut s'agir d'un test unilatéral ou bilatéral.

• Le test d'ajustement vérifie si la loi empirique (de l'échantillon) correspond à une certaine loi de probabilité attendue. Dans ce cas, la statistique du test suit la loi du χ² avec k - 1 degrés de liberté, où k est le nombre de classes dans lesquelles l'échantillon est divisé. Il s'agit d'un test unilatéral.

• Le test d'indépendance est utilisé pour déterminer s'il existe une relation statistiquement significative entre deux variables. Dans ce cas, sa statistique de test est basée sur le tableau de contingence et suit la loi du χ² avec (r - 1)(c - 1) degrés de liberté, où r est le nombre de lignes et c le nombre de colonnes dans ce tableau de contingence. Il s'agit également d'un test unilatéral.

Enfin, l'option score F doit être utilisée lorsque vous effectuez un test dans lequel la statistique du test suit la loi de Fisher, également connue sous le nom de loi de Fisher-Snedecor. La forme exacte d'une loi de Fisher dépend de deux degrés de liberté.

Pour savoir d'où viennent ces degrés de liberté, considérons les variables aléatoires indépendantes X et Y, qui suivent toutes deux la loi du χ² avec d₁ et d₂ degrés de liberté, respectivement. Dans ce cas, le rapport (X/d₁)/(Y/d₂) suit la loi de Fisher, avec (d₁, d₂) degrés de liberté. C'est pourquoi les deux paramètres d₁ et d₂ sont également appelés degrés de liberté du numérateur et du dénominateur.

La valeur p du score F est donnée par les formules suivantes, où fdr_F,d1,d2 désigne la fonction de répartition de la loi de Fisher, avec (d₁, d₂) degrés de liberté :

1. Test F unilatéral à gauche :

   valeur p = fdr_F,d1,d2(score F)

2. Test F unilatéral à droite :

   valeur p = 1 - fdr_F,d1,d2(score F)

3. Test F bilatéral :

   valeur p = 2 × min{fdr_F,d1,d2score F), 1 - fdr_F,d1,d2(score F)}

   (Avec min{a,b}, nous désignons le plus petit des nombres a et b)

Vous trouverez ci-dessous une liste des tests les plus importants qui produisent des scores F. Tous ces tests sont des tests unilatéraux à droite.

• Un test pour l'égalité des variances dans deux populations normalement distribuées. Sa statistique de test suit la loi de Fisher avec (n - 1, m - 1) degrés de liberté, où n et m sont les tailles d'échantillon respectives.

• L'analyse de la variance est utilisée pour tester l'égalité des moyennes dans trois groupes ou plus qui proviennent de populations normalement distribuées avec des variances égales. Nous obtenons la loi de Fisher avec (k - 1, n - k) degrés de liberté, où k est le nombre de groupes et n la taille d'échantillon totale (tous groupes confondus).

• Un test de signification globale de l'analyse de régression. La statistique du test a une loi de F avec (k - 1, n - k) degrés de liberté, où n est la taille d'échantillon, et k est le nombre de variables (y compris l'ordonnée à l'origine).

  Si la présence de la relation linéaire a été établie dans votre échantillon de données avec le test ci-dessus, vous pouvez calculer le coefficient de détermination, R², qui indique la force de cette relation. Vous pouvez le faire à la main ou utiliser notre calculateur du coefficient de détermination 🇺🇸.

• Un test pour comparer deux modèles de régression imbriqués. La statistique du test suit la loi de F avec (k₂ - k₁, n - k₂) degrés de liberté, où k₁ et k₂ sont les nombres de variables dans le plus petit et le plus grand modèle, respectivement, et n est la taille d'échantillon.

  Vous remarquerez peut-être que le test F de signification globale est une forme particulière du test F de comparaison de deux modèles imbriqués : il teste si notre modèle est significativement meilleur que le modèle sans prédicteur (c'est-à-dire le modèle à ordonnée à l'origine uniquement).

Non, la valeur p ne peut pas être négative. En effet, les probabilités ne peuvent pas être négatives et la valeur p est la probabilité que la statistique du test remplisse certaines conditions.

Une valeur p élevée signifie que sous l'hypothèse nulle, il y a une forte probabilité que pour un autre échantillon, la statistique de test génère une valeur au moins aussi extrême que celle observée dans l'échantillon dont vous disposez déjà. Une valeur p élevée ne vous permet pas de rejeter l'hypothèse nulle.

Une valeur p faible signifie que, sous l'hypothèse nulle, il y a peu de chances que, pour un autre échantillon, la statistique de test génère une valeur au moins aussi extrême que celle observée pour l'échantillon dont vous disposez déjà. Une valeur p faible est une preuve en faveur de l'hypothèse alternative qui vous permet de rejeter l'hypothèse nulle.