Calculateur de test de Student

Bienvenue sur notre calculateur de test de Student ! Ici, vous pouvez non seulement effectuer facilement des tests de Student à un échantillon, mais aussi des tests de Student à deux échantillons, ainsi que des tests de Student appariés. Le test de Student peut également être désigné sous le nom de test t ou test t de Student.

Recherchez-vous à trouver la valeur p du test de Student, ou plutôt ses valeurs critiques ? Ce calculateur de test de Student peut faire les deux ! 😊

« Mais à quoi sert un test de Student ? » – nous direz-vous. Eh bien, jetez un coup d'œil au texte ci-dessous pour en savoir plus. Nous vous expliquerons ce qui est réellement testé lorsque différents types de test de Student sont effectués. Nous expliquerons également quand utiliser les tests de Student (en particulier, s'il faut utiliser le test Z ou le test de Student) et quelles hypothèses vos données doivent satisfaire pour que les résultats d'un test de Student soient valides. Si vous avez toujours voulu savoir comment effectuer un test de Student à la main, nous vous fournissons la formule du test de Student nécessaire et vous expliquons comment déterminer le nombre de degrés de liberté d'un test de Student.

Le test de Student permet d'étudier la position relative des échantillons, plus précisément, il porte sur la (les) valeur(s) moyenne(s) de la (des) population(s).

Il existe différents types de test de Student que vous pouvez effectuer :

• un test de Student à un échantillon ;
• un test de Student à deux échantillons ; et
• un test de Student apparié.

Dans la section suivante, nous vous expliquons comment choisir le type de test de Student approprié. N'oubliez pas qu'un test de Student ne peut être utilisé que pour un ou deux groupes. Si vous devez comparer trois moyennes (ou plus), utilisez la méthode de l'analyse de la variance (angl. analysis of variance, ANOVA).

Le test de Student est un test paramétrique, ce qui signifie que vos données doivent satisfaire certaines hypothèses de départ :

• les points de données sont indépendants ; et
• les données, au moins approximativement, suivent une loi normale 🇺🇸.

Si votre échantillon ne satisfait pas ces hypothèses, vous pouvez recourir à des alternatives non paramétriques. Consultez notre calculateur de test U de Mann-Whitney 🇺🇸 ou le calculateur de test de la somme des rangs de Wilcoxon 🇺🇸 pour en savoir plus. Vous pouvez également utiliser le test des rangs signés de Wilcoxon ou le test des signes.

Le choix du test de Student varie selon que l'on étudie un ou deux groupes :

• Test de Student à un échantillon

  Choisissez le test de Student à un échantillon pour vérifier si la moyenne d'une population est égale à une valeur hypothétique préétablie.

  Exemples :

  1. Le volume moyen d'une boisson vendue en canettes de 0,33 L, est-il vraiment égal à 330 mL ?

  2. Le poids moyen des habitants d'une ville donnée est-il différent de la moyenne nationale ?

• Test de Student à deux échantillons

  Choisissez le test de Student à deux échantillons pour vérifier si la différence entre les moyennes de deux populations est égale à une valeur prédéterminée lorsque les deux échantillons ont été choisis indépendamment l'un de l'autre.

  En particulier, vous pouvez utiliser ce test pour vérifier si les deux groupes sont différents l'un de l'autre.

  Exemples :

  1. La différence moyenne de prise de poids entre deux groupes de personnes : un groupe suit un régime riche en glucides et l'autre un régime riche en lipides.

  2. La différence moyenne entre les résultats d'un test de mathématiques effectué par des étudiants de deux universités différentes.

  Ce test est parfois appelé test de Student à échantillons indépendants ou test de Student non apparié.

• Test de Student apparié

  Un test de Student apparié est utilisé pour étudier le changement de la moyenne d'une population avant et après une intervention expérimentale. Le test se base sur un échantillon apparié, c'est-à-dire que chaque sujet a été mesuré deux fois (avant et après l'intervention).

  En particulier, vous pouvez utiliser ce test pour vérifier si, en moyenne, une intervention a eu un effet sur la population.

  Exemples :

  1. L'évolution des résultats des étudiants à un test avant et après avoir suivi un cours.

  2. L'évolution de la pression artérielle chez les patients avant et après l'administration d'un médicament.

Vous avez atteint le stade où vous savez quel test de Student vous voulez effectuer. Maintenant, les étapes suivantes vous expliqueront comment calculer la valeur p du test de Student, ses valeurs critiques, ou même quelle décision prendre concernant l'hypothèse nulle.

1. Décidez de l'hypothèse alternative.

   • Utilisez un test bilatéral lorsque vous souhaitez simplement déterminer si la moyenne de la population (ou la différence entre les moyennes de deux populations) est différente de la valeur prédéfinie, sans tenir compte de la direction de la différence.

   • Utilisez un test unilatéral si vous voulez tester si cette moyenne (ou différence de moyennes) est supérieure ou inférieure à la valeur prédéfinie.

2. Calculez votre score T.

   Les formules pour la statistique de test dans les tests de Student incluent la taille de l'échantillon, ainsi que sa moyenne et son écart type. La formule exacte dépend du type de test de Student. Consultez les sections consacrées à chaque test pour plus de détails.

3. Déterminez les degrés de liberté pour le test de Student.

   Les degrés de liberté sont le nombre d'observations d'un échantillon qui sont libres de varier lorsque nous estimons les paramètres statistiques. Dans le cas le plus simple, le nombre de degrés de liberté est égal à votre taille d'échantillon moins le nombre de paramètres que vous devez estimer. Là encore, la formule exacte dépend du test de Student que vous souhaitez effectuer. Consultez les sections ci-dessous pour plus de détails.

Les degrés de liberté sont essentiels, car ils déterminent la loi suivie par votre score T (selon l'hypothèse nulle). S'il y a d degrés de liberté, la variable aléatoire T suit la loi de Student avec d degrés de liberté. Cette loi ressemble à la loi normale centrée réduite N(0,1) (en forme de cloche et symétrique) mais a des queues plus lourdes. Si le nombre de degrés de liberté est élevé (> 30), ce qui est généralement le cas pour les grands échantillons, la loi de Student est pratiquement impossible à distinguer de N(0,1).

Rappelons que la valeur p est la probabilité (calculée en supposant que l'hypothèse nulle est vraie) que la statistique du test produise des valeurs au moins aussi extrêmes que le score T observée pour l'échantillon. Comme les probabilités correspondent aux aires sous la courbe de la fonction de densité, la valeur p du test de Student peut être représentée graphiquement comme suit :

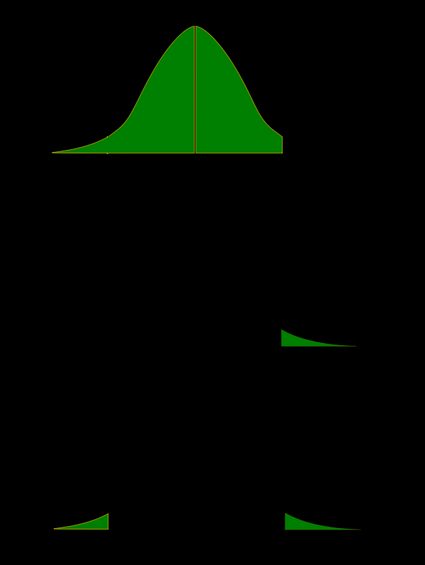
Les formules suivantes indiquent comment calculer la valeur p à partir d'un test de Student. Par fdr_t,d nous désignons la fonction de répartition de la loi de Student avec d degrés de liberté :

1. Valeur p d'un test unilatéral à gauche :

   valeur p = fdr_t,d(score T)

2. Valeur p d'un test unilatéral à droite :

   valeur-p = 1 - fdr_t,d(score T)

3. Valeur p d'un test bilatéral :

   valeur p = 2 × fdr_t,d(-|score T|)

   ou, de manière équivalente : valeur p = 2 - 2 × fdr_t,d(|score T|)

Cependant, la fonction de répartition de la loi de Student est donné par une formule quelque peu compliquée. Pour trouver la valeur p à la main, vous devez avoir recours à des tableaux statistiques, où les valeurs approximatives de la fonction de répartition sont collectées. Vous pouvez aussi utiliser des logiciels statistiques spécialisés. Heureusement, notre calculateur de test de Student détermine la valeur p du test de Student pour vous en un clin d'œil !

Rappelez-vous que dans l'approche des valeurs critiques pour les tests d'hypothèse, vous devez fixer un seuil de signification, α, avant de calculer les valeurs critiques, qui à leur tour donnent lieu à des régions critiques (également appelées zones de rejet).

Les formules pour les valeurs critiques utilisent la fonction quantile de la loi de Student, c'est-à-dire l'inverse de la fonction de répartition (fdr) :

1. Valeur critique pour un test unilatéral à gauche :
   fdr_t,d^-1(α)

   Région critique :

   (-∞, fdr_t,d^-1(α)]

2. Valeur critique pour un test unilatéral à droite :
   fdr_t,d^-1(1-α)

   Région critique :

   [fdr_t,d^-1(1-α), ∞)

3. Valeurs critiques pour un test bilatéral :
   ±fdr_t,d^-1(1-α/2)

   Région critique :

   (-∞, -fdr_t,d^-1(1-α/2)] ∪ [fdr_t,d^-1(1-α/2), ∞)

Pour décider du sort de l'hypothèse nulle, il suffit de vérifier si votre score T se situe dans la région critique.

• Si votre score T appartient à la région critique, rejetez l'hypothèse nulle et acceptez l'hypothèse alternative.

• Si votre score T se situe en dehors de la région critique, vous n'avez pas suffisamment de preuves pour rejeter l'hypothèse nulle.

1. Choisissez le type de test de Student que vous souhaitez effectuer :

   • un test de Student à un échantillon (pour tester la moyenne d'un seul groupe par rapport à une moyenne hypothétique) ;

   • un test de Student à deux échantillons (pour comparer les moyennes de deux groupes) ; ou

   • un test de Student apparié (pour vérifier comment la moyenne d'un même groupe change après une intervention).

2. Décidez de l'hypothèse alternative :

   • test bilatéral ;

   • test unilatéral à gauche ; ou

   • test unilatéral à droite.

3. Ce calculateur de test de Student vous permet d'utiliser soit l'approche de la valeur p, soit l'approche des régions critiques pour les tests d'hypothèse !

4. Entrez votre score T et le nombre de degrés de liberté. Si vous ne les connaissez pas, indiquez quelques données concernant votre (vos) échantillon(s) : taille de l'échantillon, moyenne et écart type, et notre calculateur de test de Student calculera le score T et les degrés de liberté pour vous.

5. Une fois que tous les paramètres sont remplis, la valeur p ou la région critique, apparaît immédiatement sous le calculateur de test de Student, accompagnée d'une interprétation !

1. L'hypothèse nulle est que la moyenne de la population est égale à une certaine valeur $\mu_0$.

2. L'hypothèse alternative est que la moyenne de la population est :

   • différente de $\mu_0$ ;
   • inférieure à $\mu_0$ ; ou
   • supérieure à $\mu_0$.

Formule du test de Student à un échantillon

où :

• $\mu_0$ – moyenne postulée dans l'hypothèse nulle
• $n$ – taille de l'échantillon
• $\bar{x}$ – moyenne de l'échantillon
• $\sigma$ – écart type de l'échantillon

Nombre de degrés de liberté dans le test de Student (à un échantillon) = $n-1$.

1. L'hypothèse nulle est que la différence réelle entre les moyennes de ces groupes, $\mu_1$, et $\mu_2$, est égale à une valeur prédéfinie, $\Delta$.

2. L'hypothèse alternative est que la différence $\mu_1 - \mu_2$ est :

   • différente de $\Delta$ ;
   • inférieure à $\Delta$ ; ou
   • supérieure à $\Delta$.

En particulier, si cette valeur prédéfinie est nulle ($\Delta = 0$) :

1. L'hypothèse nulle est que les moyennes de la population sont égales.

2. L'hypothèse alternative est que les moyennes de la population sont :

   • $\mu_1$ et $\mu_2$ sont différentes l'une de l'autre ;
   • $\mu_1$ est inférieure à $\mu_2$ ; et
   • $\mu_1$ est supérieure à $\mu_2$.

Formellement, pour effectuer un test de Student, nous devons en outre supposer que les variances des deux populations sont égales (cette hypothèse est appelée l'homogénéité de la variance).

Il existe une version du test de Student qui peut être appliquée sans l'hypothèse d'homogénéité de la variance : il s'agit du test t de Welch. Pour vous faciliter la tâche, nous allons décrire les deux versions.

Test de Student à deux échantillons si les variances sont égales

Utilisez ce test si vous savez que les variances des deux populations sont identiques (ou très similaires).

Formule du test de Student à deux échantillons (avec des variances égales)

où $\sigma_r$ est ce que l'on appelle l'écart type regroupé, que nous calculons comme suit :

où :

• $\Delta$ – différence moyenne postulée dans l'hypothèse nulle
• $n_1$ – taille du premier échantillon
• $\bar{x}_1$ – moyenne du premier échantillon
• $\sigma_1$ – écart type du premier échantillon
• $n_2$ – taille du deuxième échantillon
• $\bar{x}_2$ – moyenne du deuxième échantillon
• $\sigma_2$ – écart type du deuxième échantillon

Nombre de degrés de liberté dans le test de Student (deux échantillons, variances égales) = $n_1 + n_2 - 2$.

Test de Student à deux échantillons si les variances sont inégales (test t de Welch)

Utilisez ce test si les variances de vos populations sont différentes.

Formule du test t de Welch à deux échantillons (si les variances sont inégales)

où :

• $\Delta$ – différence moyenne postulée dans l'hypothèse nulle
• $n_1$ – taille du premier échantillon
• $\bar{x}_1$ – moyenne du premier échantillon
• $\sigma_1$ – écart type du premier échantillon
• $n_2$ – taille du deuxième échantillon
• $\bar{x}_2$ – moyenne du deuxième échantillon
• $\sigma_2$ – écart type du deuxième échantillon

Le nombre de degrés de liberté dans un test t de Welch (test de Student à deux échantillons avec des variances inégales) est très difficile à dénombrer. Nous pouvons l'estimer à l'aide de l'approximation de Satterthwaite :

Vous pouvez également prendre la plus petite valeur entre $n_1 - 1$ et $n_2 - 1$ comme estimation prudente du nombre de degrés de liberté.

Nous effectuons généralement un test de Student apparié lorsque nous disposons de données sur les mêmes sujets mesurées à deux reprises (avant et après une intervention). Nous désignerons les échantillons par les termes « pré-groupe » et « post-groupe ».

1. L'hypothèse nulle est que la différence réelle entre les moyennes des pré et post-populations est égale à une valeur prédéfinie, $\Delta$.

2. L'hypothèse alternative est que la différence réelle entre ces moyennes est :

   • différente de $\Delta$ ;
   • inférieure à $\Delta$ ; ou
   • supérieure à $\Delta$.

En général, cette valeur prédéfinie est égale à zéro. Nous pouvons alors reformuler les hypothèses comme suit :

1. L'hypothèse nulle est que les moyennes avant et après sont les mêmes, c'est-à-dire que l'intervention n'a pas d'impact sur la population.

2. L'hypothèse alternative est que :

   • les moyennes avant et après l'intervention sont différentes l'une de l'autre (l'intervention a un effet) ;
   • la pré-moyenne est plus petite que la post-moyenne (l'intervention augmente le résultat) ; ou
   • la pré-moyenne est supérieure à la post-moyenne (l'intervention diminue le résultat).

Formule du test de Student apparié

En fait, un test de Student apparié est techniquement identique à un test de Student à un échantillon ! Voyons pourquoi. Soit $x_1, ... , x_n$ les observations préalables et $y_1, ... , y_n$ les observations postérieures respectives. Autrement dit, $x_i, y_i$ sont les mesures avant et après du i-ème sujet.

Pour chaque sujet, calculez la différence, $d_i := x_i - y_i$. La suite se résume à un simple test de Student à un échantillon effectué sur l'échantillon des différences $d_1, ... , d_n$. Jetez un coup d'œil à la formule du score T :

où :

• $\Delta$ – différence moyenne postulée dans l'hypothèse nulle

• $n$ – taille de l'échantillon des différences (le nombre de paires)

• $\bar{x}$ – moyenne de l'échantillon des différences

• $\sigma$ – écart type de l'échantillon des différences

Nombre de degrés de liberté dans le test de Student (apparié) : $n - 1$.

Nous utilisons un test Z lorsque nous voulons tester la moyenne de la population d'un ensemble de données qui suit une loi normale et a une variance de population connue. Si le nombre de degrés de liberté est élevé, la loi de Student est très proche de N(0,1).

Par conséquent, s'il y a beaucoup de points de données (au moins 30), vous pouvez remplacer un test de Student par un test Z, et les résultats seront presque identiques. Toutefois, pour les petits échantillons dont la variance est inconnue, utilisez le test de Student, car, dans ce cas, la loi de Student diffère considérablement de la distribution N(0,1) !