Calculateur de valeur critique

Bienvenue sur le calculateur de valeur critique ! Vous pouvez ici déterminer rapidement la valeur critique pour les tests bilatéraux, ainsi que pour les tests unilatéraux à droite ou à gauche. Vous pouvez l'utiliser pour la plupart des lois statistiques : la loi normale centrée réduite N(0,1) (c'est-à-dire lorsque vous avez un score Z), t de Student, khi-deux, et F de Snedecor.

Qu'est-ce qu'une valeur critique ? Et quelle est sa formule ? Poursuivez votre lecture pour découvrir la définition de la valeur critique et nous vous guiderons ensuite dans le calcul des valeurs critiques, vous montrant comment les utiliser pour créer des zones ou régions de rejet, également appelées régions critiques.

Maintenant que vous avez trouvé notre calculateur de valeur critique, vous n'avez plus à vous soucier de savoir comment trouver la valeur critique pour toutes ces lois statistiques compliquées ! Voici ces étapes par lesquelles vous devez passer :

1. Indiquez la loi que suit votre statistique de test sous l'hypothèse nulle : s'agit-il d'une loi normale centrée réduite N(0,1), d'une loi de Student, d'une loi khi-deux ou d'une loi F de Snedecor ? Si vous n'êtes pas sûr·e, consultez les sections ci-dessous consacrées à ces distributions, et essayez de trouver le test que vous devez effectuer.

2. Choisissez l'hypothèse alternative : bilatérale, unilatérale à droite ou unilatérale à gauche.

3. Si nécessaire, spécifiez les degrés de liberté de la loi de la statistique de test. En cas de doute, consultez la description du test que vous effectuez. Pour en savoir plus sur la signification de cette quantité en statistique, consultez le calculateur de degrés de liberté.

4. Définissez le seuil de signification, $\alpha$. Nous l'avons fixé par défaut à la valeur la plus courante de 0,05, mais vous pouvez bien entendu l'adapter à vos besoins.

5. Le calculateur de valeur critique affichera alors non seulement votre ou vos valeurs critiques, mais aussi la ou les régions de rejet.

Passez-en Mode Avancé (Advanced mode) du calculateur de valeur critique si vous souhaitez augmenter la précision avec laquelle les valeurs critiques sont calculées.

Dans les tests d'hypothèses, les valeurs critiques sont l'une des deux approches qui vous permettent de décider de retenir ou de rejeter l'hypothèse nulle. L'autre approche consiste à calculer la valeur p (par exemple, en utilisant le calculateur de valeur p).

L'approche de la valeur critique consiste à vérifier si la valeur de la statistique de test générée par votre échantillon appartient à ce que l'on appelle la région de rejet ou région critique. Cette région représente l'endroit où il est hautement improbable que la statistique de test soit présente.

Une valeur critique est une valeur limite (ou deux valeurs limites dans le cas d'un test bilatéral) qui constitue la limite de la région de rejet. En d'autres termes, les valeurs critiques divisent l'échelle de votre statistique de test entre la région de rejet et la région non rejetée.

Une fois que vous avez trouvé la région de rejet, vérifiez si la valeur de la statistique de test générée par votre échantillon y appartient :

• si c'est le cas, cela signifie que vous pouvez rejeter l'hypothèse nulle et accepter l'hypothèse alternative ; ou
• si ce n'est pas le cas, cela signifie qu'il n'y a pas suffisamment de preuves pour rejeter H₀.

Mais comment calculer les valeurs critiques ? Tout d'abord, vous devez établir un seuil de signification, $\alpha$, qui quantifie la probabilité de rejeter l'hypothèse nulle lorsqu'elle est en fait correcte. Le choix de α est arbitraire ; et en pratique, on utilise le plus souvent une valeur de 0,05 ou 0,01. Les valeurs critiques dépendent également de l'hypothèse alternative que vous choisissez pour votre test, ce qui est expliqué dans la partie suivante.

Pour déterminer les valeurs critiques, vous devez connaître la loi de votre statistique de test sous l'hypothèse nulle. Les valeurs critiques sont les points à partir desquels la probabilité d'obtenir une valeur au moins aussi extrême pour la statistique de test est égale au seuil de signification α.

Quelle définition, n'est-ce pas ? Ne vous inquiétez pas, nous allons vous expliquer ce que cela signifie.

Tout d'abord, précisons que c'est l'hypothèse alternative qui détermine ce que signifie « extrême ». Notamment, dans le cas d'un test unilatéral, il n'y aura qu'une seule valeur critique. En revanche, pour un test bilatéral, deux valeurs critiques seront présentes : une à gauche et l'autre à droite de la valeur médiane selon la distribution.

Les valeurs critiques peuvent être représentées de manière pratique comme les points où l'aire sous la courbe de densité de la statistique du test à partir de ces points jusqu'aux extrémités est égale à $\alpha$.

• Test unilatéral à gauche : l'aire sous la courbe de densité de la valeur critique à gauche est égale à $\alpha$.

• Test unilatéral à droite : l'aire sous la courbe de densité de la valeur critique à droite est égale à $\alpha$.

• Test bilatéral : l'aire sous la courbe de densité à partir de la valeur critique à gauche est égale à $\alpha/2$, et l'aire sous la courbe à partir de la valeur critique à droite est également égale à $\alpha/2$ ; ainsi, l'aire totale est égale à $\alpha$.

Comme vous pouvez le constater, trouver les valeurs critiques pour un test bilatéral avec un seuil de signification de $\alpha$ revient à trouver les deux valeurs critiques unilatérales avec un seuil de signification de $\alpha/2$.

Les formules pour les valeurs critiques impliquent la fonction quantile, $Q$, qui est l'inverse de la fonction de répartition ($\mathrm{fdr}$) pour la distribution de la statistique du test (calculée sous l'hypothèse que H₀ tient !) : $Q = \mathrm{fdr}^{-1}$.

Une fois que vous aurez choisi une valeur pour $\alpha$, les formules de valeurs critiques seront les suivantes :

1. Test unilatéral à gauche :

2. Test unilatéral à droite :

3. Test bilatéral :

Dans le cas d'une distribution symétrique par rapport à 0, les valeurs critiques pour le test bilatéral sont également symétriques :

Malheureusement, les lois de probabilité les plus répandues dans les tests d'hypothèses ont des formules $\mathrm{fdr}$ quelque peu compliquées. Pour trouver les valeurs critiques à la main, il vous faudrait utiliser des logiciels spécialisés ou des tables statistiques. Dans ces cas, la meilleure option est, bien sûr, d'utiliser notre calculateur de valeur critique ! 😁

Utilisez l'option Z (normale centrée réduite) si la statistique de votre test suit (au moins approximativement) la loi normale centrée réduite N(0,1).

Dans les formules ci-dessous, $u$ désigne la fonction quantile de la distribution normale centrée réduite N(0,1) :

1. Valeur critique de Z pour un test unilatéral à gauche : $u(\alpha)$

2. Valeur critique de Z pour un test unilatéral à droite : $u(1-\alpha)$

3. Valeur critique de Z pour un test bilatéral : $\pm u(1- \alpha/2)$

Consultez le calculateur de test Z 🇺🇸 pour en savoir plus sur le test Z, comme son utilisation pour le calcul de la moyenne d'une population. Il existe également des tests Z pour la différence entre deux moyennes de population, en particulier entre deux proportions.

Utilisez l'option test de Student si votre statistique de test suit la loi de Student. Cette loi est semblable à la loi normale centrée réduite de N(0,1), mais ses extrémités sont plus épaisses et leurs formes exactes dépendent du nombre de degrés de liberté. Si ce nombre est élevé (> 30), ce qui est généralement le cas pour les grands échantillons, la loi de Student est pratiquement impossible à distinguer de la loi normale centrée réduite N(0,1). Consultez notre calculateur de statistiques du test de Student pour déterminer la statistique du test correspondant.

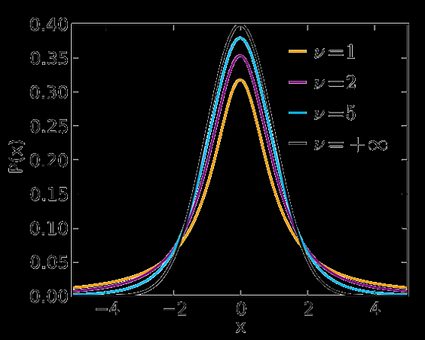
Dans les formules ci-dessous, $Q_{\text{t}, d}$ est la fonction quantile de la loi de Student avec $d$ degrés de liberté :

1. Valeur critique de t pour un test unilatéral à gauche : $Q_{\text{t}, d}(\alpha)$

2. Valeur critique de t pour un test unilatéral à droite : $Q_{\text{t}, d}(1 - \alpha)$

3. Valeurs critiques de t pour un test bilatéral : $\pm Q_{\text{t}, d}(1 - \alpha/2)$

Consultez le calculateur de test de Student pour obtenir des informations détaillées sur divers tests de Student : celui pour une moyenne de population, avec un écart type de population inconnue, ceux pour la différence entre les moyennes de deux populations (avec des écarts types de population égaux ou inégaux), ainsi que le test de Student pour échantillons appariés.

Utilisez l'option χ² (khi-deux) pour effectuer un test dont la statistique suit la loi du χ².

Vous devez déterminer le nombre de degrés de liberté de la loi du χ² de votre statistique de test. Ci-dessous, nous les énumérons les tests du χ² les plus couramment utilisés.

Nous donnons ici les formules pour les valeurs critiques du khi-deux ; $Q_{\chi^2, d}$ est la fonction quantile suivant la loi du χ² avec $d$ degrés de liberté :

1. Valeur critique du χ² pour un test unilatéral à gauche : $Q_{\chi^2, d}(\alpha)$ 

2. Valeur critique du χ² pour un test unilatéral à droite : $Q_{\chi^2, d}(1 - \alpha)$ 

3. Valeurs critiques du χ² pour un test bilatéral : $Q_{\chi^2, d}(\alpha/2)$ et $Q_{\chi^2, d}(1 - \alpha/2)$

Plusieurs tests différents aboutissent à un score de χ².

• Le test d'adéquation : la loi empirique correspond-elle à la loi attendue ?

  Ce test est unilatéral à droite. Sa statistique de test suit la loi du χ² avec $k - 1$ degrés de liberté, où $k$ est le nombre de sous-groupes dans lesquelles l'échantillon est divisé.

• Le test d'indépendance : existe-t-il une relation statistiquement significative entre deux variables ?

  Ce test est également unilatéral à droite et sa statistique est calculée à partir du tableau de contingence. Il y a $(l - 1)(c - 1)$ degrés de liberté, où $l$ est le nombre de lignes et $c$ le nombre de colonnes du tableau de contingence.

• Le test de la variance pour des données normalement distribuées : cette variance a-t-elle une valeur prédéterminée ?

  Ce test peut être unilatéral ou bilatéral. Sa statistique de test suit la loi du χ² avec $n - 1$ degrés de liberté, où $n$ est la taille de l'échantillon.

Enfin, choisissez F (Fisher-Snedecor) si votre statistique de test suit la loi F de Snedecor. Cette loi a une paire de degrés de liberté.

Voyons comment ces degrés de liberté apparaissent. Supposons que vous ayez deux variables aléatoires indépendantes, $X$ et $Y$, qui suivent chacune la loi du χ² avec $d_1$ et $d_2$ degrés de liberté, respectifs. Si vous considérez maintenant le ratio $(\frac{X}{d_1}):(\frac{Y}{d_2})$, il s'avère qu'il suit la loi F de Snedecor avec $(d_1, d_2)$ degrés de liberté. C'est la raison pour laquelle nous appelons $d_1$ et $d_2$ les degrés de liberté du numérateur et du dénominateur, respectivement.

Dans les formules ci-dessous, $Q_{\text{F}, d_1, d_2}$ représente la fonction quantile suivant la loi F de Snedecor avec $(d_1, d_2)$ degrés de liberté :

1. Valeur critique de F pour un test unilatéral à gauche : $Q_{\text{F}, d_1, d_2}(\alpha)$

2. Valeur critique de F pour un test unilatéral à droite : $Q_{\text{F}, d_1, d_2}(1 - \alpha)$

3. Valeurs critiques de F pour un test bilatéral : $Q_{\text{F}, d_1, d_2}(\alpha/2)$ et $Q_{\text{F}, d_1, d_2}(1 -\alpha/2)$

Nous énumérons ici les tests les plus importants produisant des scores F : chacun d'entre eux est unilatéral à droite.

• ANOVA : teste l'égalité des moyennes dans trois groupes ou plus qui proviennent de populations suivant la loi normale avec des variances égales. Il y a $(k - 1, n - k)$ degrés de liberté, où $k$ est le nombre de groupes et $n$ la taille totale de l'échantillon (pour chaque groupe).

• Signification statistique globale dans l'analyse de régression. La statistique du test a $(k - 1, n - k)$ degrés de liberté, où $n$ est la taille de l'échantillon, et $k$ est le nombre de variables (y compris l'ordonnée à l'origine).

• Comparez deux modèles de régression imbriqués. La statistique du test suit la loi F de Snedecor avec $(k_2 - k_1, n - k_2)$ degrés de liberté, où $k_1$ et $k_2$ sont le nombre de variables dans le modèle le plus petit et le modèle le plus grand, respectivement, et $n$ est la taille d'échantillon.

• L'égalité des variances dans deux populations normalement distribuées. Il y a $(n - 1, m - 1)$ degrés de liberté, où $n$ et $m$ sont les tailles d'échantillon respectives.

Une valeur critique de Z est la valeur qui définit la région critique dans les tests d'hypothèse lorsque la statistique du test suit la loi normale centrée réduite. Si la valeur de la statistique du test tombe dans la région critique, vous devez rejeter l'hypothèse nulle et accepter l'hypothèse alternative.

Pour trouver une valeur critique de Z pour un niveau de confiance donné α :

1. Vérifiez si vous effectuez un test unilatéral ou bilatéral.

2. Pour un test unilatéral :

   • à gauche : la valeur critique est le quantile α-ième suivant la loi normale centrée réduite N(0,1) ;

   • à droite : la valeur critique est le quantile (1-α)-ième quantile.

3. Test bilatéral : la valeur critique est égale à ±(1-α/2)-ième quantile suivant la loi normale centrée réduite N(0,1).

4. Pas de tables des quantiles ? Utilisez les tables de la fonction de répartition ! (La fonction quantile est l'inverse de la fonction de répartition).

5. Vérifiez votre réponse à l'aide d'un calculateur de valeur critique en ligne (tel que celui-ci).

En théorie, non. En pratique, très souvent, oui. La loi de Student est similaire à la loi normale centrée réduite, mais ces dernières ne sont pas les mêmes. Cependant, si le nombre de degrés de liberté (autrement dit la taille de votre échantillon) est suffisamment grand (> 30), alors les deux distributions sont pratiquement indiscernables, et donc la valeur critique de t a pratiquement la même valeur que la valeur critique de Z.

La valeur critique de Z pour un intervalle de confiance de 95 % est :

• 1,96 pour un test bilatéral 
• 1,64 pour un test unilatéral à droite 
• -1,64 pour un test unilatéral à gauche