Calculateur de volume d'une pyramide à base triangulaire
Notre calculateur de volume d'une pyramide à base triangulaire vous permet de trouver le volume de toute pyramide dont la base forme un triangle, que vous connaissiez ou non l'aire de sa base. Si vous souhaitez déterminer le volume d'une pyramide droite à base triangulaire ou d'un tétraèdre régulier, vous êtes au bon endroit.
Vous avez besoin de savoir trouver le volume d'une pyramide à base triangulaire à la main ? Poursuivez votre lecture ! Nous vous donnerons la formule ainsi que des exemples d'utilisation.
Quelle est la formule du volume d'une pyramide à base triangulaire ?
La formule du volume de la pyramide à base triangulaire est :
V = A × h / 3
où :
V– le volume de la pyramide à base triangulaireA– l'aire de la base de la pyramideh– la hauteur entre la base et le sommet
En d'autres termes, le volume d'une pyramide à base triangulaire est un tiers du produit de l'aire de la base et de la hauteur de la pyramide.
💡 La formule du volume de la pyramide à base triangulaire repose sur les formules utilisées dans nos calculateur de volume d'une pyramide et calculateur de volume d'un cône.
Comment trouver le volume d'une pyramide à base triangulaire à la main ?
Pour trouver le volume d'une pyramide à base triangulaire d'une hauteur de 10 cm, dont la base est un triangle droit de 3 cm, 4 cm et 5 cm de côté, vous devez :
- Déterminer l'aire de la base : ici, elle est de
3 × 4 / 2 = 6. - Trouver la hauteur de la pyramide : dans notre cas, c'est
10. - Appliquez la formule du volume de la pyramide à base triangulaire :
6 × 10 / 3 = 20. - Le volume est 20 cm3.
L'étape la plus difficile est généralement le calcul de l'aire de la base. Pour en savoir plus, vous pouvez consulter notre calculateur d'aire d'un triangle quelconque ou l'un des calculateurs dédiés à chaque type de triangle :
- Calculateur de triangle équilatéral
- Calculateur de triangle isocèle
- Calculateur d'aire d'un triangle rectangle
Si vous souhaitez savoir comment trouver le volume d'une pyramide à base triangulaire qui est un tétraèdre régulier ou une pyramide droite à base triangulaire, consultez les deux sections restantes où nous donnons les formules appropriées.
Le volume d'un tétraèdre
Une pyramide à base triangulaire dont les faces sont des triangles équilatéraux est appelée tétraèdre régulier.

Le volume d'un tétraèdre dont le côté est de longueur a peut être exprimé comme suit :
V = a³ × √2 / 12
Ce volume est approximativement égal à V = 0,12 × a³.
Par exemple, le volume d'un tétraèdre de 6 cm de côté est égal à :
V = 6³ × √2 / 12 = 18 √2
Ce qui peut être approximé par 0,12 × 6³ = 25,92.
Le volume d'une pyramide droite à base triangulaire
Une pyramide est droite si son sommet est directement au-dessus du centroïde de la base. Dans le cas contraire, la pyramide est dite oblique. Si, en outre, la base est un triangle équilatéral, les formules suivantes pour le volume s'appliquent.
-
Si la base a des côtés de longueur a et que la hauteur de la pyramide est h, alors :
V = a² × h × √3 / 12 -
Si la base a des côtés de longueur a et que les arêtes entre la base et le sommet ont une longueur b, à l'aide du théorème de Pythagore, nous pouvons trouver la hauteur de la pyramide et ensuite le volume :
V = √(b² - a²/3) × a² × √3 / 12
FAQ
Comment trouver le côté d'un tétraèdre en fonction de son volume ?
Pour déterminer le côté d'un tétraèdre à partir de son volume :
- Multipliez le volume par 12.
- Divisez le résultat par
√2 ≈ 1,41. - Prenez la racine cubique.
- Et c'est tout ! Vous avez trouvé le côté de votre tétraèdre.
Quelle est la hauteur d'un tétraèdre en fonction de son volume ?
La réponse est 1,665 4 × ∛volume. Nous obtenons ce résultat en fusionnant les formules : hauteur = √(2/3) × côté et volume = a³ × √2 / 12, ce qui donne la formule hauteur = √(∛576 / 3) × ∛volume. Approximativement, nous obtenons hauteur ≈ 1,665 4 × ∛volume, comme indiqué.
Comment utiliser notre calculateur de volume d'une pyramide à base triangulaire ?
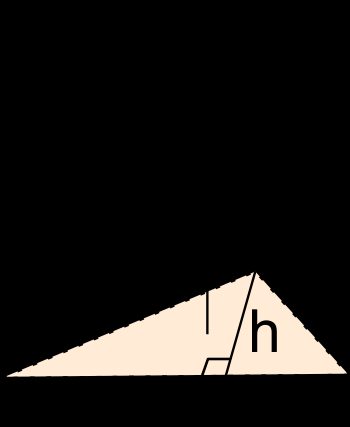
Une pyramide à base triangulaire est un objet solide formé en reliant une base triangulaire à un point, appelé apex (le sommet). Cela crée quatre faces, chacune d'entre elles étant un triangle. En faisant pivoter la pyramide, on remarque que chaque face peut jouer le rôle de la base de la pyramide. Le segment perpendiculaire à la base et passant par le sommet est la hauteur de la pyramide.
Ici, le triangle bleu foncé est la base de la pyramide, et le segment noir en pointillés en est la hauteur :
Pour utiliser notre calculateur de volume d'une pyramide à base triangulaire, suivez ces étapes :
Entrez la hauteur de la pyramide.
Le calculateur de volume d'une pyramide à base triangulaire vous donnera alors le volume de votre pyramide. :)