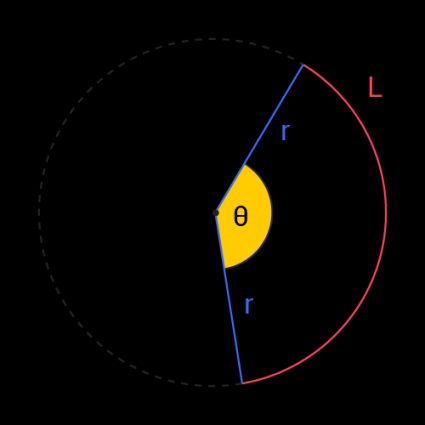
¿Te has preguntado alguna vez cómo hallar el ángulo central de un círculo? La calculadora del ángulo central está aquí para ayudarte; las únicas variables que necesitas son la longitud de arco y el radio.
Sigue leyendo para aprender la definición de ángulo central y cómo utilizar la fórmula del ángulo central.
¿Qué es un ángulo central?
Un ángulo central es un ángulo con vértice en el centro de un círculo cuyos brazos se extienden hasta la circunferencia. Puedes imaginar que el ángulo central está en la punta de una porción de pizza en una gran pizza circular.
Puedes hallar el ángulo central de un círculo mediante la fórmula:
θ = L / r
donde θ es el ángulo central en radianes, L es la longitud de arco y r es el radio.
¿De dónde procede la fórmula del ángulo central?
La simplicidad de la fórmula del ángulo central tiene su origen en la definición de radián. Un radián es una unidad de tamaño angular, donde 1 radián se define como un ángulo central (θ) cuya longitud de arco es igual al radio (L = r).
La calculadora del ángulo del círculo en términos de pizza
Como las matemáticas pueden dar hambre, podríamos entender mejor el ángulo central en términos de pizza. Lo creas o no, las pizzas son estupendas para explicar las matemáticas de un círculo, como puedes ver en nuestra calculadora del tamaño de una pizza 🇺🇸. ¿Cuál sería el ángulo central de una porción de pizza si la longitud de la corteza () fuera igual al radio ()?
Como el problema define , y sabemos que radian se define como el ángulo central cuando , podemos ver que el ángulo central es radian. También podríamos utilizar la fórmula del ángulo central de la siguiente manera:
¿Cuántas porciones de pizza con un ángulo central de 1 radián podrías cortar de una pizza circular?
En una pizza circular completa, sabemos que los ángulos centrales de todas las porciones sumarán 2π radianes = 360°. Como cada porción tiene un ángulo central de radian, necesitaremos porciones o porciones para llenar un círculo completo.
Llegamos a la misma respuesta si pensamos en este problema en términos de la corteza de la pizza: calcular la circunferencia de un círculo es . Como la longitud de la corteza = radio, entonces cortezas cabrán a lo largo del perímetro de la pizza.
Ahora, si aún tienes hambre, echa un vistazo a la calculadora del área de un sector circular para calcular el área de cada trozo de pizza
Desafío extra: ¿Qué distancia recorre la Tierra en cada estación?
Intenta utilizar la calculadora del ángulo central a la inversa para resolver este problema. La Tierra está aproximadamente a 149.6 millones de km del Sol. Si la Tierra recorre aproximadamente un cuarto de su órbita cada estación, ¿cuántos km recorre la Tierra cada estación (por ejemplo, de primavera a verano)?
Abordemos este problema paso a paso:
-
Simplifica el problema suponiendo que la órbita de la Tierra es circular (La órbita de la Tierra es en realidad elíptica y cambia constantemente). En este modelo, el Sol está en el centro del círculo, y la órbita de la Tierra es la circunferencia.
-
El radio es la distancia entre la Tierra y el Sol: millones de km.
-
El ángulo central es un cuarto de círculo: .
-
Utiliza la calculadora del ángulo central para hallar la longitud de arco.
Puedes probar tú mismo el cálculo final reordenando la fórmula como:
A continuación, convierte el ángulo central en radianes (utiliza nuestro convertidor de ángulos 🇺🇸 si no recuerdas cómo hacerlo), y resuelve la ecuación:
¡Cuando suponemos que para una órbita perfectamente circular, la Tierra recorre aproximadamente 234.9 millones de km cada estación!
Preguntas frecuentes
¿Cómo hallo el ángulo central de un círculo?
Para hallar el ángulo central de un círculo, utiliza la fórmula:
θ = L / r
donde:
θ- ángulo central en radianes;L- longitud de arco;r- radio del círculo.
Para hallar el ángulo central de un círculo, tienes que calcular el cociente entre la longitud de arco y el radio de un círculo.
Puedes imaginar que el ángulo central está en la punta de una porción de pizza en una gran pizza circular.
¿Cómo encuentro el radio con la longitud de arco y el ángulo central?
Para hallar un radio con longitud de arco y ángulo central, tienes que calcular el cociente entre la longitud de arco y el ángulo central.