Calculadora de la ley de Snell

Cuando la luz viaja de un medio a otro, se "dobla" o refracta. La calculadora de la ley de Snell te permite explorar este tema en detalle y comprender los principios de la refracción. Sigue leyendo para descubrir cómo se formula la ley de Snell de la refracción y qué ecuación te permitirá calcular el ángulo de refracción. La última parte de este artículo está dedicada a la fórmula y definición del ángulo crítico.

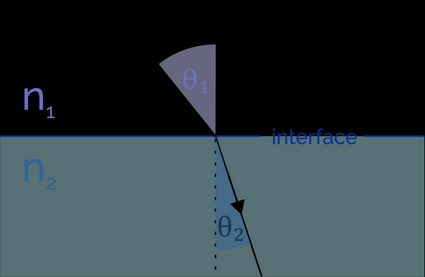
La ley de Snell describe cómo funciona exactamente la refracción. Cuando un rayo de luz entra en un medio distinto, su velocidad y longitud de onda cambian. El rayo se curva hacia la normal entre dos medios (cuando su velocidad disminuye) o se aleja de ella (cuando su velocidad aumenta). El ángulo de refracción depende de los índices de refracción de ambos medios:

donde:

• $n_1$ es el índice de refracción del medio 1 (desde el que viaja el rayo);
• $n_2$ es el índice de refracción del medio 2 (hacia el que viaja el rayo);
• $\theta_1$ es el ángulo de incidencia: el ángulo entre una línea normal (perpendicular) a la frontera entre dos medios y el rayo entrante;
• $\theta_2$ es el ángulo de refracción: el ángulo entre la normal a la frontera y el rayo que atraviesa el medio 2.

Puedes encontrar algunos de los valores de $n_1$ y $n_2$ para medios comunes en la calculadora del índice de refracción.

En general, la ley de refracción de Snell sólo es válida para medios isótropos. En los anisótropos, como el espato de Islandia, el rayo puede dividirse en dos rayos.

Supongamos que quieres hallar el ángulo de refracción de un rayo de luz que viaja de aire a vidrio. El ángulo de incidencia es de 30°.

1. Halla el índice de refracción del aire. Es igual a $1.000293$.
2. Halla el índice de refracción del vidrio. Supongamos que es igual a $1.50$.
3. Transforma la ecuación de modo que la incógnita (ángulo de refracción) esté en el lado izquierdo: $\text{sen}(\theta_2) = \frac{n_1 \text{sen}(\theta_1)}{n_2}$.
4. Realiza los cálculos: $\text{sen}(\theta_2) = \frac{1.000293 \text{sen}(30\degree)}{1.50} = 0.333$.
5. Halla el arcoseno de este valor: $\theta_2 = \text{arcsen}(0.333) = 19.48 \degree$.
6. También puedes ahorrarte algo de tiempo y utilizar simplemente la calculadora de la ley de Snell.

A veces, al aplicar la ley de refracción de Snell, recibirás el $\text{sen}(\theta_2)$ como valor superior a 1. Esto es, por supuesto, imposible. Si esto ocurre, significa que toda la luz se refleja en el borde (este fenómeno se conoce como reflexión interna total). Nuestra calculadora de la ley de Snell te avisará cuando esto ocurra.

El ángulo de incidencia más alto, para el que la luz no se refleja, se denomina ángulo crítico. El rayo refractado recorre el borde entre ambos medios. Esto significa que el ángulo de refracción es igual a 90°. Por tanto, puedes hallar el ángulo crítico mediante la siguiente ecuación:

Tras la sustitución, $n_1 \text{sen}(\theta_1) = n_2 \cdot 1$.

Resolviendo para el ángulo de incidencia, $\theta_1 = \text{arcsen}(\frac{n_2}{n_1})$.