Calculadora de la frecuencia de resonancia LC

Si quieres calcular la frecuencia de resonancia de un circuito LC, no busques más: esta calculadora de frecuencia de resonancia LC es la herramienta que necesitas. Introduce la inductancia y la capacitancia y en un abrir y cerrar de ojos encontrarás la frecuencia resonante y angular. También proporcionamos algo de teoría, ya que puede ser útil; a continuación encontrarás cómo calcular la frecuencia de resonancia, así como una breve definición sobre qué es realmente la frecuencia de resonancia.

Si te interesan los circuitos electrónicos, probablemente te gustaría saber cómo obtener alguna fracción de la tensión de entrada; nuestra calculadora de un divisor de tensión 🇺🇸 es imprescindible para esa tarea.

Un circuito LC (también llamado circuito resonante, u oscilador LC) es un circuito RLC idealizado de resistencia cero. ¡Si buscas un circuito "no ideal", dirígete a nuestra calculadora de circuitos RLC 🇺🇸!

Un circuito LC sólo contiene un inductor y un condensador, en serie o en paralelo:

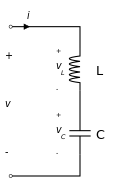
Los circuitos resonantes se suelen utilizar como generadores de señales y filtros paso banda, lo que significa que seleccionan una señal con una frecuencia determinada a partir de una señal más compleja. Se aplican ampliamente en electrónica: puedes encontrar circuitos LC en amplificadores, osciladores, sintonizadores, transmisores y receptores de radio. Los circuitos LC y RC pueden utilizarse para filtrar una señal bloqueando determinadas frecuencias.

La frecuencia de resonancia es la frecuencia natural, no amortiguada, de un sistema. Si aplicamos una frecuencia resonante, las oscilaciones se convierten en la máxima amplitud, e incluso fuerzas relativamente pequeñas pueden producir grandes amplitudes. Sin embargo, si se elige cualquier otra frecuencia, esa señal se amortigua.

Existen muchos tipos diferentes de resonancias, por ejemplo:

• mecánicas y acústicas,
• eléctricas,
• ópticas,
• orbitales, y
• moleculares.

En los circuitos LC, la frecuencia de resonancia viene determinada por la capacitancia C y la impedancia L.

Para calcular la frecuencia de resonancia de un circuito compuesto por un inductor y un condensador, sigue estos pasos:

1. Escribe la capacitancia C en faradios.

2. Escribe la inductancia L en henrios.

3. Introduce ambos parámetros en la fórmula de la frecuencia resonante:

   f = 1 / (2π × √(L × C))

Donde:

• $f$ — la frecuencia de resonancia,
• $L$ — la inductancia del circuito, y
• $C$ — la capacitancia del circuito.

¿De dónde procede esta fórmula? La resonancia en el circuito LC aparece cuando la reactancia inductiva del inductor se iguala a la reactancia capacitiva del condensador. Por tanto:

Entonces, tras transformar la ecuación, hallamos:

Entonces:

Y por último:

Además, la frecuencia angular puede calcularse a partir de la siguiente fórmula, bien conocida:

Utilizar nuestra herramienta es un paseo por el parque:

1. Introduce el valor del condensador. Por ejemplo, nuestra capacidad es igual a $1\ \mathrm{μF}$.
2. Escribe la inductancia. Nuestra inductancia en nuestro circuito LC es igual a $0.18\ \mathrm{mH}$.
3. ¡La calculadora de frecuencia de resonancia ha hecho su trabajo! Hemos determinado rápidamente cuál es la frecuencia de resonancia: 11.863 kHz. También puedes comprobar la frecuencia angular, ya que el valor aparecerá debajo.

Una calculadora de frecuencias de resonancia es una herramienta flexible, así que (como siempre) puedes escribir dos variables cualesquiera, y la que falte se calculará en un instante.