Calculadora de deflexión en vigas
Esta calculadora de deflexión en vigas te ayudará a determinar la deflexión máxima de vigas simplemente apoyadas y en voladizo que soportan configuraciones de carga simples.
Puedes elegir entre una selección de tipos de carga que pueden actuar sobre cualquier longitud de viga que desees. La magnitud y la ubicación de estas cargas afectan la deflexión de la viga.
En esta calculadora de deflexión en vigas, te familiarizarás con las diversas fórmulas de deflexión en vigas utilizadas para calcular las deflexiones de vigas simplemente apoyadas y las deflexiones de vigas en voladizo. También aprenderás cómo el módulo de elasticidad de la viga y su momento de inercia de área transversal afectan la deflexión máxima de la viga.
La deflexión de una viga es una parte importante del análisis de vigas, pero otra parte importante es el análisis de esfuerzos. El módulo de sección es una herramienta poderosa para estudiar los esfuerzos por flexión de las vigas, y lo puedes calcular con nuestra calculadora de módulo de sección 🇺🇸.
¿Qué es la deflexión en vigas?

En la construcción de edificios, solemos utilizar estructuras de armazón que se mantienen en su sitio gracias a los cimientos en el suelo. Estas estructuras son como los esqueletos de los edificios, casas e incluso puentes. En una estructura, llamamos columnas a los elementos verticales y vigas a los horizontales. Las vigas son los miembros alargados de una estructura que soportan las cargas aportadas por los forjados horizontales de las estructuras, como los forjados de hormigón macizo, los sistemas de vigas de piso 🇺🇸 de madera y los tejados.
Cuando las vigas soportan cargas demasiado pesadas, comienzan a doblarse. Llamamos a la cantidad de flexión de la viga deflexión de la viga. La deflexión de una viga es el desplazamiento vertical de un punto a lo largo del centroide de una viga. También podemos considerar la superficie de la viga como nuestro punto de referencia, siempre y cuando no se produzcan cambios en la altura o profundidad de la viga durante la flexión.
Cómo calcular la deflexión máxima de una viga
Hemos equipado nuestra calculadora de deflexión en vigas con las fórmulas que utilizan los ingenieros y estudiantes de ingeniería para determinar rápidamente la deflexión máxima que experimentará una viga específica debido a la carga que soporta. Sin embargo, estas fórmulas solo pueden resolver cargas simples y combinaciones de estas cargas. Hemos tabulado estas fórmulas para ti, como se muestra a continuación:
Fórmulas de deflexión en vigas simplemente apoyadas
Casos de viga y carga | Ecuación de deflexión máxima de la viga () |
|---|---|
 | |
 | |
 | |
 | |
 | |
 |
Fórmulas de deflexión en vigas en voladizo
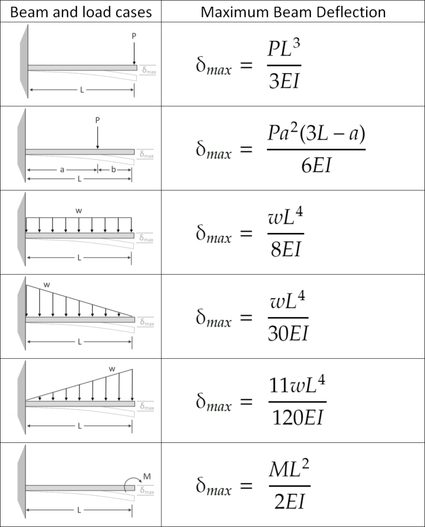
Método de superposición
Para calcular la deflexión máxima de una viga con una combinación de cargas, podemos recurrir al método de superposición. El método de superposición afirma que podemos estimar la deflexión total de una viga sumando todas las deflexiones provocadas por cada configuración de carga. Sin embargo, este método solo nos da un valor aproximado de la deflexión máxima real. Para calcular deflexiones en casos de cargas más complejas, tendríamos que emplear el método de doble integración.
Rigidez de la viga
Calcular la flexión de una viga requiere conocer la rigidez de la viga y la cantidad de fuerza o carga que influiría en la flexión de la viga. Podemos definir la rigidez de la viga multiplicando su módulo de elasticidad, E, por su momento de inercia, I.
El módulo de elasticidad depende del material de la viga. Cuanto mayor sea el módulo de elasticidad de un material, más flexión podrá soportar antes de llegar a su punto de rotura. El módulo de elasticidad del concreto se encuentra entre 15 y 50 GPa (gigapascales), mientras que el del acero tiende a estar alrededor de 200 GPa o más. Esta diferencia en los valores del módulo de elasticidad indica que el concreto solo puede soportar una cantidad limitada de deflexión y experimentará agrietamiento antes que el acero.
Puedes obtener más información sobre el módulo de elasticidad consultando nuestra calculadora de esfuerzo. Por otro lado, para determinar el momento de inercia de área de la sección transversal de una viga, puedes visitar nuestra calculadora de momento de inercia 🇺🇸. El momento de inercia de área representa la resistencia que opone un material al movimiento de rotación y depende de las dimensiones de la sección transversal del material.
El momento de inercia de área también varía en función del eje sobre el que gira el material. Para comprender mejor este concepto, consideremos la sección transversal de una viga rectangular de 20 cm de anchura y 30 cm de altura. Utilizando las fórmulas que también puedes ver en nuestra calculadora de momento de inercia de área, podemos calcular los valores del momento de inercia de esta sección transversal de la siguiente manera:
Iₓ = ancho × alto³ / 12
Iₓ = 20 × (30³)/12
Iₓ = 45 000 cm⁴
Iᵧ = alto × ancho³ / 12
Iᵧ = 30 × (20³)/12
Iᵧ = 20 000 cm⁴
Observa que existen dos valores para el momento de inercia. Esto se debe a que podemos considerar que la viga se dobla verticalmente a lo largo de su longitud (o experimenta un momento flector alrededor del eje x) y lateralmente a lo largo de su longitud (o se dobla alrededor del eje y). Como estamos considerando la flexión de la viga cuando se dobla verticalmente o alrededor del eje x, tenemos que utilizar Iₓ para nuestros cálculos.
Los valores del momento de inercia que obtuvimos nos indican que la viga es más resistente a la flexión con una carga vertical y más susceptible a la flexión si se somete a una carga lateral horizontal. Esta diferencia en los valores del momento de inercia de área es la razón por la cual vemos vigas en esta configuración, en la cual su altura es mayor que su ancho.
Comprender las fórmulas de deflexión en vigas
Ahora que conocemos los conceptos de módulo de elasticidad y momento de inercia, podemos entender por qué estas variables se encuentran en el denominador de nuestras fórmulas de deflexión en vigas. Las fórmulas nos indican que, cuanto más rígida sea la viga, menor será su deflexión. Sin embargo, al analizar detenidamente nuestras fórmulas, también podemos afirmar que la longitud de la viga tiene un impacto directo en su deflexión. Cuanto más larga sea una viga, su capacidad para doblarse aumenta y, por ende, la deflexión también incrementa.
En cuanto a las cargas, estas influyen en la deflexión de la viga de dos maneras: en la dirección y en la magnitud de la deflexión. Las cargas que actúan hacia abajo tienden a provocar una deflexión en esa misma dirección. Estas cargas pueden ser cargas puntuales, cargas distribuidas o momentos aplicados. Las fórmulas de esta calculadora se enfocan exclusivamente en las direcciones hacia arriba o hacia abajo para las cargas puntuales y las cargas distribuidas. Las cargas distribuidas se asemejan a una presión, pero solo consideran la longitud de la viga y no su anchura.
Además, las fórmulas de esta calculadora también tienen en cuenta el momento o torsión, ya sea en sentido horario o antihorario. Solo tienes que consultar las direcciones de las flechas en la imagen correspondiente de la fórmula para determinar en qué dirección tiene un valor de carga positivo.
Ejemplo de cálculo de la deflexión de una viga

Para un ejemplo de cálculo de la flexión de una viga, consideremos un simple banco de madera con patas separadas 1.5 m una de otra en sus centros. Supongamos que el asiento de este banco es una tabla de pino blanco del este, con 4 cm de grosor y 30 cm de ancho, y que actúa como el asiento de este banco. Podemos tratar este asiento como si fuera una viga que se dobla cuando alguien se sienta en el banco. Dadas las dimensiones de este asiento, podemos calcular su momento de inercia de área, siguiendo el mismo enfoque que describimos anteriormente. Como necesitamos calcular Iₓ, su momento de inercia de área sería:
Iₓ = ancho × alto³ / 12
Iₓ = 30 × (4³)/12
Iₓ = 160.0 cm⁴ o 1.6×10⁻⁶ m⁴
El pino blanco oriental tiene un módulo de elasticidad de 6800 MPa (6.8×10⁹ Pa), que es el valor que obtuvimos del . También puedes obtener fácilmente el valor del módulo de elasticidad de otros materiales, como el acero y el hormigón, en internet o en tu biblioteca local. Ahora que conocemos estos valores, consideremos la carga que soportará este banco. Supongamos que un niño de 400 N se sienta en el centro del banco. Ahora podemos calcular la deflexión que experimentará el asiento del banco debido a una carga puntual en su centro:
δmáx = P × L³ / (48 × E × I)
δmáx = (400 N) × (1.5 m)³ / (48 × 6.8×10⁹ Pa × 1.6×10⁻⁶ m⁴)
δmáx = 0.002585 m = 2.5850 mm
Esto significa que el banco se hundirá unos 2.6 milímetros respecto a su posición original cuando el niño se siente en el centro del banco.
Si este tema te ha parecido interesante y te gustaría saber más sobre la resistencia de los materiales, puede que también te guste nuestra calculadora de factor de seguridad 🇺🇸.
Preguntas frecuentes
¿Qué es la deflexión en ingeniería?
La deflexión en ingeniería se refiere al desplazamiento de una viga con respecto a su posición original. Este desplazamiento puede originarse a partir de fuerzas, ya sea del propio miembro o de una fuente externa, como el peso de las paredes o el tejado. La deflexión en ingeniería es una medida de longitud, ya que al calcularla, obtenemos un ángulo o distancia que se relaciona con el desplazamiento de la viga.
¿Cuál es la fórmula general de la deflexión de una viga?
Las fórmulas generales para la deflexión de vigas son PL³/(3EI) para vigas en voladizo, y 5wL⁴/(384EI) para vigas simplemente apoyadas, donde P es la carga puntual, L es la longitud de la viga, E representa el módulo de elasticidad, e I se refiere al momento de inercia de área. Sin embargo, muchas otras fórmulas de deformación permiten estudiar diferentes tipos de configuraciones.
¿Cómo puedo calcular la deflexión de una viga?
Para calcular la deflexión de una viga sigue estos pasos:
- Determina si se trata de una viga en voladizo o de una viga simplemente apoyada.
- Mide la deformación de la viga a partir de la deformación de la estructura.
- Elige la fórmula de deflexión de la viga adecuada para tu tipo de viga.
- Introduce tus datos incluyendo la longitud de la viga, el momento de inercia de área, el módulo de elasticidad y la fuerza actuante.
¿Qué causa la deflexión en las vigas?
Las principales causas de la deflexión incluyen el peso aplicado sobre la estructura, el momento de inercia de área, que está relacionado con el tamaño de la sección transversal, la longitud de la estructura no soportada y el material de la estructura.
¿Cuál es la deflexión central de una viga simplemente apoyada de 4 m?
3.47 mm, si la longitud (L) es 4 m = 4 × 10³ mm, la carga puntual (P) es 45 × 10³ N, el módulo de elasticidad (E) es 2.4 × 10⁵ N/mm², y el momento de inercia de área (I) es 72 × 10⁶ mm⁴. Para calcularlo:
- Elige la fórmula: PL³/(48EI).
- Introduce los valores:
45 × 10³ × (4 × 10³)³/(48 × 2.4 × 10⁵ × 72 × 10⁶) = 3.47 mm.
