Konfidenzintervall Rechner

Dieser Konfidenzintervall-Rechner ist ein Tool, mit dem du das Konfidenzintervall für eine Stichprobe ermitteln kannst, wenn du den Mittelwert 🇺🇸, die Standardabweichung und die Größe deiner Stichprobe angibst. Du kannst ihn für ein beliebiges Konfidenzniveau verwenden. Wenn du wissen möchtest, was genau das Konfidenzintervall ist und wie es berechnet wird, oder wenn du nach der Formel für das 95%-Konfidenzintervall für einen z-Wert suchst, wird dir dieser Artikel weiterhelfen.

Laut Definition: „Ein Konfidenzintervall ist ein aus der Stichprobenstatistik abgeleiteter Wertebereich, der wahrscheinlich den Wert eines unbekannten Parameters enthält.“ Aber was bedeutet das in der Praxis?

Stell dir vor, ein Ziegelhersteller macht sich Gedanken darüber, ob die Masse der von ihm hergestellten Ziegel den Vorgaben entspricht. Er hat die durchschnittliche Masse einer Stichprobe von 100 Ziegeln gemessen – sie beträgt 3 kg. Er hat außerdem festgestellt, dass das 95%ige Konfidenzintervall zwischen 2,85 kg und 3,15 kg liegt. Das bedeutet, dass er zu 95% sicher sein kann, dass die durchschnittliche Masse aller von ihm hergestellten Ziegel zwischen 2,85 kg und 3,15 kg liegt. Genauer gesagt: Wenn der Ziegelhersteller viele verschiedene Stichproben von je 100 Ziegeln genommen und aus jeder Stichprobe das Konfidenzintervall berechnet hätte, dann würden 95% dieser Intervalle den wahren Mittelwert der Ziegelmasse enthalten.

Natürlich willst du nicht immer zu genau 95% sicher sein. Vielleicht willst du zu 99% sicher sein, oder es reicht dir, dass das Konfidenzintervall in 90% der Fälle richtig ist. Diesen Prozentsatz nennt man das Konfidenzniveau.

Für die Berechnung des Konfidenzintervalls musst du drei Parameter deiner Stichprobe kennen: den Mittelwert μ, die Standardabweichung σ und den Stichprobenumfang n (Anzahl der Werte, die du gemessen hast). Dann kannst du den Standardfehler 🇺🇸 und anschließend den absoluten Fehler nach den folgenden Formeln berechnen:

Standardfehler = σ/√n

Absoluter Fehler = Standardfehler * Z(0,95)

wobei Z(0,95) der z-Score ist, der dem Konfidenzniveau von 95% entspricht. Der z-Score ist ein standardisierter Wert, welcher in unserem Fall den auf die Standardnormalverteilung standardisierten Grenzwert für den 95%-Konfidenzniveau-Bereich ausdrückt. Wenn du ein anderes Konfidenzniveau verwendest, musst du anstelle dieses Wertes den entsprechenden z-Score berechnen. Aber keine Sorge, unser Z-Score-Rechner macht es dir leicht!

Wie findet man den Z(0,95)-Wert? Das ist der Wert des z-Scores, bei dem das Konfidenzniveau gleich 95% ist. Das heißt, wenn du eine Kurve der Normalverteilung zeichnest, ist die Fläche zwischen den beiden z-Werten gleich 0,95 (von 1).

Wenn du diesen Wert mithilfe einer z-Score-Tabelle berechnen möchtest, tue Folgendes:

1. Entscheide dich für ein Konfidenzniveau. Nehmen wir an, es ist 95%.
2. Berechne, wie hoch die Wahrscheinlichkeit ist, dass dein Ergebnis nicht im Konfidenzintervall liegen wird. Dieser Wert ist gleich 100% - 95% = 5%.
3. Wirf einen Blick auf die Normalverteilungskurve. 95% sollte der Fläche zwischen den beiden Werten entsprechen. Das bedeutet, dass der Bereich links vom Gegenwert deines z-Scores gleich 0,025 (2,5% der Gesamtfläche) ist und der Bereich rechts von deinem z-Score ebenfalls gleich 0,025 (2,5% der Gesamtfläche) ist.
4. Der Bereich rechts von deinem z-Score ist genau der gleiche wie der p-Wert deines z-Scores. Du kannst die z-Score-Tabellen verwenden, um den z-Score zu finden, der dem p-Wert von 0,025 entspricht. In diesem Fall ist es 1,959.

Sobald du den Z(0,95)-Wert berechnet hast, kannst du diesen Wert einfach in die obige Gleichung einsetzen, um den absoluten Fehler zu erhalten. Jetzt musst du nur noch die untere und obere Grenze des Konfidenzintervalls bestimmen:

untere Grenze = Mittelwert - absoluter Fehler

obere Grenze = Mittelwert + absoluter Fehler

Um ein (zweiseitiges) Konfidenzintervall zu berechnen, befolge diese Schritte:

1. Nehmen wir an, der Stichprobenumfang ist 100.
2. Finde den Mittelwert deiner Stichprobe. Nehmen wir an, er ist gleich 3.
3. Bestimme die Standardabweichung der Stichprobe. Nehmen wir an, sie beträgt 0,5.
4. Wähle das Konfidenzniveau. Das gebräuchlichste Konfidenzniveau ist 95%.
5. In der statistischen Tabelle findest du den Z(0,95)-Score, d. h. das 97,5-%-Quantil von N(0,1) – in unserem Fall ist es 1,959.
6. Berechne den Standardfehler als σ/√n = 0,5/√100 = 0,05.
7. Multipliziere diesen Wert mit dem z-Score, um den absoluten Fehler zu erhalten: 0,05 ∙ 1,959 = 0,098.
8. Addiere und subtrahiere den absoluten Fehler vom Mittelwert, um das Konfidenzintervall zu erhalten. In unserem Fall liegt das Konfidenzintervall zwischen 2,902 und 3,098.

Das war's! Das war eine ganze Menge an Berechnungen, oder? Zum Glück kann unser Konfidenzintervall-Rechner all diese Berechnungen selbstständig durchführen.

Eine besondere Art, Konfidenzintervalle zu nutzen, ist die Zeitreihenanalyse, bei der der Stichprobendatensatz eine Folge von Beobachtungen in einem bestimmten Zeitrahmen darstellt.

Ein häufiger Gegenstand einer solchen Untersuchung ist die Frage, ob sich die Veränderung einer Variable auf eine andere Variable auswirkt.

Um genauer zu sein, betrachten wir die folgende allgemeine Frage, die Ökonomen oft beschäftigt: „Wie wirkt sich eine Änderung des Zinssatzes auf den Preis aus?“

Es gibt mehrere Möglichkeiten, sich dieser Frage zu nähern, die eine komplexe theoretische und empirische Analyse erfordert, die den Rahmen dieses Textes bei weitem sprengen würde. Auch wenn es mehrere Techniken zur Schätzung und Anwendung von Konfidenzintervallen gib, können wir anhand dieses Beispiels die Funktionsweise von Konfidenzintervallen in einem komplizierteren Problem darstellen.

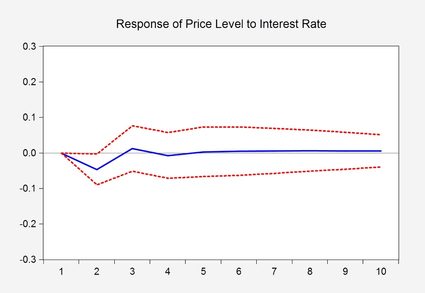
Das obige Diagramm ist eine visuelle Darstellung eines Schätzergebnisses eines ökonometrischen Modells, einer sogenannten Impulsantwortfunktion, die die Reaktion einer Variablen auf eine Veränderung der anderen Variablen zeigt. Die roten gestrichelten Linien unter und über der blauen Linie stellen ein 95%-Konfidenzintervall dar, das einen Bereich mit den wahrscheinlichsten Ergebnissen definiert. Genauer gesagt zeigt es, dass nach einer Änderung des Zinssatzes erst im zweiten Monat eine signifikante Reaktion auf der Preisebene eintritt.

Zusammenfassend hoffen wir, dass du mit den obigen Beispielen und der kurzen Beschreibung einen besseren Einblick in den Zweck des Konfidenzintervalls bekommst und keine Probleme damit hast, unseren Konfidenzintervall-Rechner zu verwenden.

Wenn du wiederholt Stichproben ziehst und für jede von ihnen das 95%-Konfidenzintervall für den Mittelwert der Stichprobe ermittelst, dann wird der wahre Mittelwert der Grundgesamtheit in etwa 95% dieser Konfidenzintervalle enthalten sein. Die restlichen 5% der Intervalle enthalten nicht den wahren Mittelwert der Population.

Der z-score für ein zweiseitiges 95%-Konfidenzintervall ist 1,959, was dem 97,5-%-Quantil der Standardnormalverteilung N(0,1) entspricht.

Der z-score für ein zweiseitiges 99%-Konfidenzintervall ist 2,807, das ist das 99,5-%- Quantil der Standardnormalverteilung N(0,1).

Die Breite eines Konfidenzintervalls vergrößert sich, wenn der absolute Fehler zunimmt, was geschieht, wenn:

• das Signifikanzniveau steigt,
• der Stichprobenumfang sinkt oder
• die Varianz der Stichprobe zunimmt.

Die Breite eines Konfidenzintervalls nimmt ab, wenn sich der absolute Fehler verringert, was geschieht, wenn:

• das Signifikanzniveau sinkt,
• der Stichprobenumfang steigt oder
• die Varianz der Stichprobe abnimmt.

Der Stichprobenmittelwert hat keinen Einfluss auf die Breite eines Konfidenzintervalls!