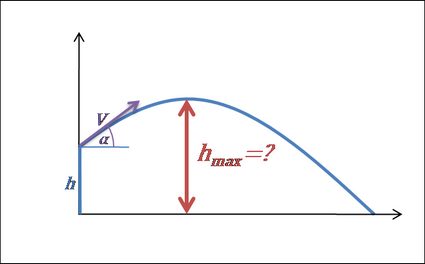
Maximale Höhe Rechner – Wurfparabel

Der Rechner für die maximale Höhe ist ein Hilfsmittel zur Bestimmung der maximalen vertikalen Position eines geworfenen Objekts in einer parabolischen Bewegung. Egal, ob du die Formel für die maximale Höhe eines Objekts benötigst, das direkt vom Boden oder von einer bestimmten Anfangshöhe startet – wir haben die Lösung für dich. Wenn du dich immer noch fragst, wie man die maximale Höhe eines geworfenen oder abgeschossenen Objekts ermittelt, lies die beiden kurzen Absätze unten, dann sollte alles klar werden.

Die maximale Höhe des geworfenen Objekts ist die höchste vertikale Position entlang seiner Flugbahn. Das Objekt fliegt nach oben, bevor es den höchsten Punkt erreicht – und nach diesem Punkt fällt es nach unten. Das bedeutet, dass die vertikale Geschwindigkeit am höchsten Punkt der Wurfparabel gleich $0$ ($v_y = 0$) ist.

Aus dieser Gleichung können wir die Zeit $t_{\mathrm{h}}$ ermitteln, die benötigt wird, um die maximale Höhe $h_{\mathrm{max}}$ zu erreichen:

Die Formel für den vertikalen Abstand lautet:

Mit $y = h_{\mathrm{max}}$ und $t = t_{\mathrm{h}}$ können wir diese beiden Gleichungen miteinander verbinden:

Und was ist, wenn wir ein geworfenes Objekt von einer bestimmten Anfangshöhe $h$ abschießen? Keine Sorge! Die Berechnungen sind ein Kinderspiel – du musst nur diese Anfangshöhe addieren!

Lass uns einige Sonderfälle mit unterschiedlichen Abschusswinkeln besprechen:

• Wenn $\alpha = 90\degree$, dann vereinfacht sich die Formel zu:

Und die Flugzeit ist die längste.

Wenn außerdem $v_y = 0$ gilt, handelt es sich um den freien Fall, den wir im Freier Fall Rechner ausführlich beschrieben haben. Du möchtest vielleicht auch einen Blick auf unser noch genaueres Äquivalent werfen – den Freier Fall mit Luftwiderstand Rechner 🇺🇸.

• Wenn $\alpha = 45\degree$, dann kann die Gleichung wie folgt geschrieben werden:

Und in diesem Fall ist die Reichweite maximal, wenn du vom Boden aus startest ($h = 0$).

• Wenn $\alpha = 0\degree$, dann ist die vertikale Geschwindigkeit gleich $0$ ($v_y = 0$). In diesem Fall können wir die horizontale Bewegung des geworfenen Objekts berechnen. Da der Sinus von $0\degree$ gleich $0$ ist, verschwindet der zweite Teil der Gleichung, und wir erhalten:

Die Anfangshöhe, aus der wir das Objekt abschießen, ist die maximale Höhe in der parabolische Bewegung.

Die parabolische Bewegung eines geworfenen Objekts ist ein klassisches Problem der Physik, das unter allen möglichen Aspekten analysiert wurde. Die Tatsache, dass wir sie leicht reproduzieren und beobachten können, hat dazu beigetragen. Wir haben uns entschlossen, eine Reihe von Werkzeugen für dieses Problem zu entwickeln:

• Der Wurfparabel Rechner für eine umfassende Analyse des Problems;

• Den Flugbahn Rechner 🇺🇸, um das Problem als geometrische Funktion zu analysieren; und

• Eine Reihe spezifischer Werkzeuge:

  • Der Wurfweite Rechner 🇺🇸;
  • Der Flugzeit Rechner – Wurfparabel 🇺🇸; und
  • Der Waagerechter Wurf Rechner 🇺🇸 (für $\alpha=0$).

Entspann dich und sieh dir an, wie einfach dieser Rechner für die maximale Höhe zu bedienen ist:

1. Wähle die Geschwindigkeit des geworfenen Objekts. Geben wir $9\ \mathrm{m/s}$ ein.

2. Gib den Winkel ein. Angenommen, wir schießen einen Ball ⚽ in einem Winkel von $70\degree$ nach oben.

3. Optional kannst du die Anfangshöhe eingeben. In unserem Fall ist unsere Startposition der Boden, also gib $0$ ein. Kann der Ball über einen $4\ \mathrm{m}$ Zaun fliegen?

4. Hier ist sie – Der Maximale-Höhe-Rechner hat die Antwort! Sie lautet $3,\!65\ \mathrm{m}$. Er wird also nicht über den Zaun fliegen – Schieße ihn etwas härter oder erhöhe den Winkel, um dein Ziel zu erreichen.

Denke daran, dass wir den Luftwiderstand nicht mit einbeziehen!