Wurfparabel Rechner

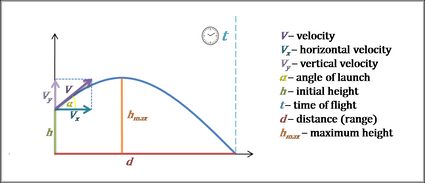
Unser Wurfparabel-Rechner ist ein Werkzeug, das dir hilft, die parabolische Flugbahn eines Objekts zu analysieren. Er kann die Flugzeit, aber auch die Komponenten der Geschwindigkeit, die Reichweite des Objekts und die maximale Flughöhe ermitteln. Lies weiter, wenn du verstehen möchtest, wie eine Wurfparabel aussieht, was ein schiefer Wurf ist, und du die oben genannten Werte mithilfe der Bewegungsgleichungen bestimmen möchtest.

Du schaust lieber zu als zu lesen? In nur 90 Sekunden erfährst du mit diesem Video alles, was du zu wissen brauchst:

Stell dir vor, ein Bogenschütze schießt einen Pfeil in die Luft. Er steigt auf und bewegt sich vorwärts, mit einer gewissen Neigung zum Boden. Je weiter er fliegt, desto langsamer wird sein Aufstieg – und schließlich beginnt er zu sinken, bewegt sich nun nach unten und vorwärts und schlägt schließlich wieder auf dem Boden auf. Wenn du seinen Weg nachzeichnen könntest, ergäbe das eine Kurve – eine Wurfparabel. Übrigens haben wir auch einen Pfeilgeschwindigkeitsrechner, der die Bewegung von Pfeilen analysiert – probiere ihn aus!

Auf den Körper wirkt in dem Fall nur eine Kraft – die Schwerkraft. Der Luftwiderstand wird bei den Berechnungen vernachlässigt. Wenn du ein Kräftediagramm für diese Situation zeichnen würdest, müsstest du nur einen nach unten zeigenden Vektor einzeichnen und ihn als „Schwerkraft“ bezeichnen. Würden noch andere Kräfte auf den Körper wirken, würde es sich nach Definition nicht um einen freien Fall handeln und wir würden nicht die gleiche parabolische Flugbahn erhalten.

Die Flugbahn eines schiefen Wurfs ist ziemlich logisch. Nehmen wir an, du kennst die Anfangsgeschwindigkeit des Objekts $v$, den Abwurfwinkel $\alpha$ und die Anfangshöhe $h$. Unser Wurfparabel-Rechner folgt diesen Schritten, um alle übrigen Parameter zu ermitteln:

1. Berechne die Komponenten der Geschwindigkeit.

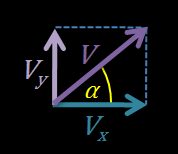
• Die horizontale Komponente der Geschwindigkeit $v_\mathrm x$ ist gleich $v \cos\alpha$.
• Die vertikale Komponente der Geschwindigkeit $v_\mathrm y$ ist gleich $v \sin\alpha$.
• Die drei Vektoren – $v$, $v_\mathrm x$ und $v_\mathrm y$ – bilden ein rechtwinkliges Dreieck.

Wenn die vertikale Geschwindigkeitskomponente gleich 0 ist, dann handelt es sich um einen horizontalen Wurf. Wenn zudem α = 90° entspricht, sprechen wir oft von einem freien Fall (Achtung: Man bezieht sich mit dem Begriff „freier Fall“ oft auf genau diese Art Bewegung. Eigentlich heißt aber freier Fall nur, dass keine Kräfte außer die Schwerkraft auf das Objekt wirken. Der Begriff umfasst also mehrere Arten von Bewegung). Wir haben beide Probleme im Waagerechter Wurf Rechner 🇺🇸 bzw. im Freier Fall Rechner gelöst.

2. Schreibe die Bewegungsgleichungen auf.

Entfernung

• Die horizontal zurückgelegte Strecke kann durch $x = v_\mathrm x t$ ausgedrückt werden, wobei $t$ die Zeit ist.
• Die vertikale Entfernung vom Boden wird durch die Formel $y = h + v_\mathrm{y0} t - g t^2 / 2$ beschrieben, wobei $g$ die Erdbeschleunigung und $v_\mathrm{y0}$ die vertikale Anfangsgeschwindigkeit ist.

Geschwindigkeit

• Die horizontale Geschwindigkeit ist gleich $v_\mathrm x$.
• Die vertikale Geschwindigkeit kann als $v_\mathrm y = v_\mathrm{y0} - g t$ ausgedrückt werden.

Beschleunigung

• Die horizontale Beschleunigung ist gleich 0.
• Die vertikale Beschleunigung ist gleich $-g$ (weil nur die Schwerkraft auf das geworfene Objekt wirkt).

3. Berechne die Flugzeit.

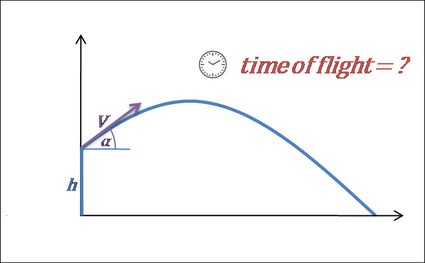
• Der Flug endet, wenn das Objekt auf den Boden trifft. Wir können sagen, dass dies der Fall ist, wenn der vertikale Abstand zum Boden gleich 0 ist. Für den Fall, dass die Anfangshöhe 0 ist, kann die Formel wie folgt geschrieben werden: $v_\mathrm{y0} t - g t^2 / 2 = 0$. Aus dieser Gleichung ergibt sich dann, dass die Flugzeit beträgt:

• Wenn wir den Gegenstand jedoch aus einer gewissen Höhe werfen, dann ist die Formel nicht mehr so schön reduziert wie zuvor, und wir erhalten eine quadratische Gleichung, die wir lösen müssen: $h + v_\mathrm{y0} t - g t^2 / 2 = 0$. Nachdem wir diese Gleichung gelöst haben, erhalten wir:

4. Berechne die Reichweite des Körpers

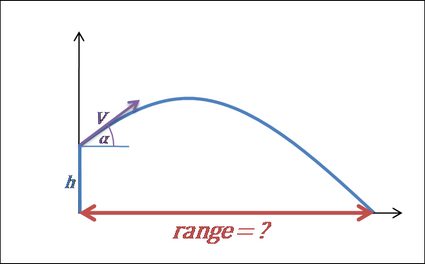
• Die Reichweite des Objekts ist die gesamte horizontale Entfernung, die während der Flugzeit zurückgelegt wird. Wenn wir das Objekt vom Boden aus werfen (Anfangshöhe = 0), können wir die Formel als $R = v_\mathrm x t = v_\mathrm x \cdot 2 \cdot v_\mathrm{y0} / g$ schreiben. Sie kann auch in die folgende Form umgewandelt werden: $R = v^2_0 \sin(2\alpha) / g$

• Die Sache wird komplizierter, wenn die Anfangshöhe von 0 abweicht. Dann müssen wir die lange Formel aus dem vorherigen Schritt als $t$ einsetzen:

• Die Reichweite ist in der Ballistik besonders wichtig. Wir sprechen das Thema im Ballistischer Koeffizient Rechner 🇺🇸 an.

5. Berechne die maximale Höhe.

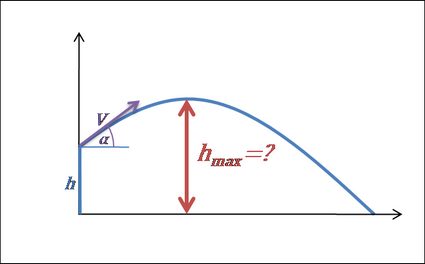
• Wenn der Körper die maximale Höhe erreicht, hört er auf, sich nach oben zu bewegen und beginnt zu fallen. Das bedeutet, dass seine vertikale Geschwindigkeitskomponente von positiv zu negativ wechselt – mit anderen Worten, sie ist zum Zeitpunkt $t(v_\mathrm y=0)$ für einen kurzen Moment gleich 0.
• Wenn $v_\mathrm {y0} - g t(v_\mathrm y=0) = 0$, dann können wir diese Gleichung in $t(v_\mathrm y=0) = v_\mathrm{y0} / g$ umformulieren.
• Jetzt müssen wir nur noch die vertikale Entfernung vom Boden zu diesem Zeitpunkt bestimmen:

• Wenn wir ein Objekt von einer bestimmten Anfangshöhe $h$ werfen, müssen wir diesen Wert einfach in die endgültige Formel einsetzen:

Uff, das war eine Menge an Berechnungen! Fassen wir das mal zusammen, um die wichtigsten Gleichungen für den schiefen Wurf in einem Abschnitt zu sammeln:

1. Abwurf des Objekts vom Boden (Anfangshöhe h = 0):

• Horizontale Geschwindigkeitskomponente: $v_\mathrm x = v_0 \cos \alpha$
• Vertikale Geschwindigkeitskomponente: $v_\mathrm y = v_0 \sin \alpha - gt$
• Flugzeit: $t = 2 v_\mathrm{y0} / g$
• Reichweite des Objekts: $R = 2 v_\mathrm x v_\mathrm{y0} / g$
• Maximale Höhe: $h_\mathrm{max} = v^2_\mathrm{y0} / (2 g)$

2. Abwurf des Objekts von einer bestimmten Höhe (Anfangshöhe h > 0):

• Horizontale Geschwindigkeitskomponente: $v_\mathrm x = v_0 \cos \alpha$
• Vertikale Geschwindigkeitskomponente: $v_\mathrm y = v _0 \sin \alpha - gt$
• Flugzeit: $t = \left[v_\mathrm{y0} + \sqrt{v^2_\mathrm{y0} + 2 g h}\right] / g$
• Reichweite des Objekts: $R = v_\mathrm x \left[v_\mathrm{y0} + \sqrt{v^2_\mathrm{y0} + 2 g h}\right] / g$
• Maximale Höhe: $h_\mathrm{max} = h + v^2_ \mathrm{y0} / (2 g)$

Mit unserem Wurfparabel-Rechner sparst du sicher eine Menge Zeit. Er kann auch in umgekehrter Richtung rechnen. Gib zum Beispiel die Flugzeit, die Entfernung und die Anfangshöhe für dein Objekt ein und sieh zu, wie er alle Berechnungen für dich erledigt!

Schau dir auch den Parabel Rechner an, um mehr über eine solche Kurve aus mathematischer Sicht zu erfahren.