Willkommen bei unserem Vektor-Rechner! Er hilft dir, eine ganze Reihe von Vektoroperationen durchzuführen und zu verstehen. Hast du die kartesischen Koordinaten von zwei Vektoren oder kennst du nur ihre Vektorrichtung und den Vektorbetrag? Vielleicht musst du den Vektor zwischen zwei Punkten finden? Dieser Vektor-Rechner kann mit all diesen Situationen umgehen; er führt folgendes durch:
- Vektor Addition;
- Vektor Subtraktion;
- Vektor Multiplikation (sowohl Vektorprodukt als auch Skalarprodukt!); und
- Vektor Projektionen.
Außerdem lernst du, was die Vektornorm (Einheitsvektor) ist und wie man einen Vektor normiert.
Orthogonale Koordinaten
In einem orthogonalen (sogenannten kartesischen) xy-Koordinatensystem beschreiben wir den Vektor a in einer zweidimensionalen Ebene durch seine kartesischen Koordinaten:
a = [ax, ay].
Diese Koordinaten beruhen auf der horizontalen Verschiebung entlang des Vektors a nach ax entlang der x-Achse und einer vertikalen Verschiebung ay entlang der y-Achse.
Auf ähnliche Weise beschreiben wir Vektoren im dreidimensionalen Raum mithilfe des kartesischen xyz-Systems mit drei Zahlen:
a = [ax, ay, az],
die den Verschiebungen entlang der x-, y- bzw. z-Achse entsprechen.
Vektorrichtung und Vektorbetrag
Wir können einen ebenen Vektor auch mit den Begriffen Vektorrichtung und Vektorbetrag beschreiben. Der Vektorbetrag ist die Länge eines Vektors (auch Betrag genannt) und die Richtung eines Vektors ist der Winkel zwischen der horizontalen Achse und dem Vektor.
Seien [ax, ay] die kartesischen Koordinaten eines Vektors mit dem Vektorbetrag m und der Richtung θ. Um ein Set von Koordinaten in das andere umzuwandeln, verwendest du die folgenden Formeln:
ax = m × cos(θ)
ay = m × sin(θ)
Wie bestimmt man einen Vektor zwischen zwei Punkten?
Wenn du einen Vektor zwischen zwei Punkten bestimmen möchtest, d.h. zwischen dem Anfangs- und dem Endpunkt, ziehst du einfach die Koordinaten des Endpunkts vom Anfangspunkt ab:
-
Anfangspunkt (Ursprung): a = [ax, ay, az]
-
Endpunkt (Spitze/Kopf): b = [bx, by, bz]
-
Vektor zwischen diesen beiden Punkten:
[bx - ax, by - ay, bz - az]
Schauen wir uns ein Beispiel an:
-
Anfangspunkt:
[1, 2, 3] -
Endpunkt:
[1, 1, -1] -
Vektor zwischen diesen beiden Punkten:
[1 - 1, 1 - 2, 3 - (-1)] = [0, -1, 4]
Wie normiert man einen Vektor? Was ist der Einheitsvektor?
Bei der Vektornormierung wird ein Vektor einfach so gestaucht, dass er einen einheitlichen Vektorbetrag hat. Denke daran, dass die Richtung des Vektors beibehalten werden muss!
Um den Einheitsvektor zu bestimmen, musst du seinen Betrag mithilfe des Satzes von Pythagoras berechnen. Der Betrag des Vektors ist seine Länge: die Quadratwurzel aus der Summe des Quadrats der Koordinaten deines Vektors. Teile dann jede Koordinate des ursprünglichen Vektors durch seine Länge. Vielleicht möchtest du auch den Vektorbetrag Rechner 🇺🇸 verwenden, um den Betrag deines Vektors zu bestimmen. Das ist eine vereinfachte Version dieses Vektorrechners.
Beispiel:
Sei a = [2, 3, 4]. Wir möchten den Einheitsvektor von a finden:
|a| = √(4 + 9 + 16) = √29
Die Normierung von a liefert uns den Vektor a/|a| = [2/√29, 3√29, 4/√29]. Wusstest du, dass wir einen Einheitsvektor Rechner haben?
Wie benutze ich diesen Vektor-Rechner?
Um den Vektor-Rechner zu benutzen, befolge folgende Schritte:
- Sag uns, ob du mit ebenen Vektoren (2D) oder räumliche Vektoren (3D) arbeitest.
- Entscheide dich für die Vektor-Operation, die du durchführen möchtest. Du kannst zwischen Vektoraddition oder -subtraktion, Vektormultiplikation (Skalarprodukt oder Vektorprodukt), Normierung, Vektorprojektion oder dem Finden des Vektors zwischen zwei Punkten wählen.
- Gib deine Daten ein. Bei ebenen Vektoren kannst du zwischen kartesischen Koordinaten oder Vektorrichtung und Vektorbetrag wählen.
- Unser Vektor-Rechner liefert dir deine Ergebnisse. Viel Spaß! 😊
Vektor Addition
-
In orthogonalen Koordinaten können wir die [Vektoraddition](calc: 3426) durchführen, indem wir einfach die entsprechenden Koordinaten der Vektoren addieren:
für a = [ax, ay, az],
und b = [bx, by, bz],
haben wir a + b = [ax + bx, ay + by, az + bz].
Beispiel:
Die Summe von
a = [2, 3, 4]undb = [1, -2, 3]ist:a + b = [2 + 1, 3 + (-2), 4 + 3] = [3, 1, 7] -
Graphische Methode: Wenn wir für zwei Vektoren
aundbdie Vektorsummea + bberechnen möchten, legen wir den Ursprung vonban die Spitze vona. Der resultierende Vektor geht vom Ursprung vonabis zur Spitze vonb. Wir bezeichnen diesen mathematischen Satz als Parallelogrammgleichung:
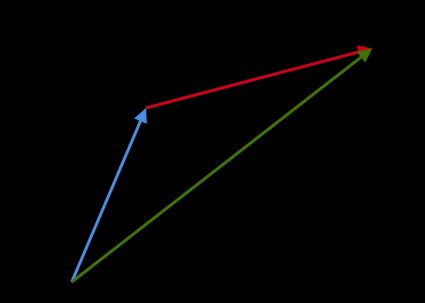
Die Subtraktion von Vektor b von Vektor a ist einfach die Addition von -b zu a. Um den Vektor -b zu ermitteln, nimm du die Koordinaten von b mit entgegengesetztem Vorzeichen; ändere Pluszeichen in Minuszeichen und Minuszeichen in Pluszeichen:
wenn b = [1, -2, 4],
dann -b = [-1, 2, -4]
-
Folglich führen wir bei orthogonalen Koordinaten die Vektorsubtraktion
a - bdurch, indem wir die Koordinaten vonbvon denen vonasubtrahieren:wenn a = [ax, ay, az]
und b = [bx, by, bz],
dann a - b = [ax - bx, ay - by, az - bz].
Beispiel:
Die Differenz von
a = [2, 3, 4]undb = [1, -2, 3]ist gegeben durcha - b = [2 - 1, 3 - (-2), 4 - 3] = [1, 5, 1]. -
Graphische Methode: Wir erhalten die Vektordifferenz
a - b, indem wir die Spitze vonban die Spitze vonasetzen und einen Vektor vom Ursprung vonazum Ursprung vonbzeichnen:
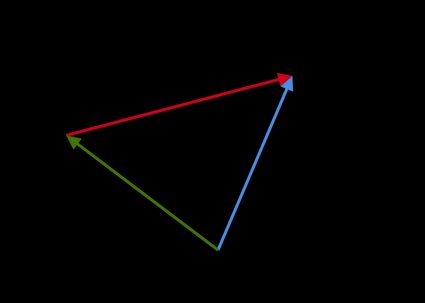
Vektor Multiplikation
Sei vorsichtig, wenn du Vektoren multiplizierst; es gibt verschiedene Arten der Vektormultiplikation! Die bekanntesten sind das Kreuzprodukt (Vektorprodukt) und das Skalarprodukt, die wir im Folgenden beschreiben:
Vektormultiplikation — Kreuzprodukt
Das Kreuzprodukt wird mit einem Malkreuz × als Multiplikationskreuz geschrieben und bezeichnet das Entnehmen zweier Vektoren und die Rückgabe eines anderen Vektors.
Die Formel lautet wie folgt:
a × b = |a| × |b| × sin(θ) × n,
wobei:
θ— Winkel zwischenaundb;aundb— Vektorbeträge vonaundb; undn— Einheitsvektor, der senkrecht zuaundbsteht, bestimmt durch die Rechte-Hand-Regel.
Rechte-Hand-Regel:
Halte deine rechte Hand so, dass dein Zeigefinger auf den Vektor
aund dein Mittelfinger auf den Vektorbzeigt: dein Daumen zeigt die Richtung des Vektorproduktsa × ban.
- Grafische Interpretation: Der resultierende Vektor
a × bsteht im rechten Winkel (senkrecht) zu den Ausgangsvektoren, und sein Vektorbetrag ist gleich dem Flächeninhalt eines Parallelogramms, das von den Ausgangsvektoren aufgespannt wird:
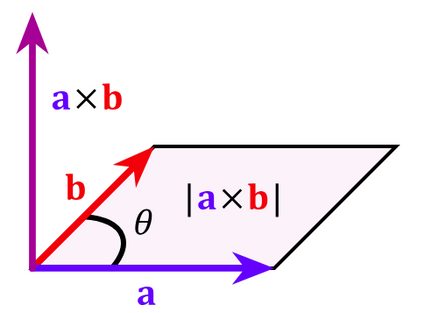
-
In Bezug auf orthogonale Koordinaten:
für a = [ax, ay, az],
und b = [bx, by, bz], haben wir
a × b = [ay×bz - az×by, az×bx - ax×bz, ax×by - ay×bx].
Beispiel:
Das Vektorprodukt von
a = [2, 3, 4]undb = [1, -2, 3]ist gleich:a × b = [3 × 3 - 4 × (-2), 4 × 1 - 2 × 3, 2 × (-2) - 3 × 1] = [17, -2, -7]. -
Ja, die Formel sieht ein bisschen einschüchternd aus. Man kann sie sich aber leichter merken, wenn man weiß, dass die Koordinaten des Produkts die Determinanten der entsprechenden 2 x 2-Matrizen sind:
- Die erste Koordinate ist:



-
Achte auf die Reihenfolge der Vektoren, denn im Gegensatz zum Skalarprodukt kommt es beim Vektorprodukt auf die Reihenfolge an! Genauer gesagt haben wir
b × a = - a × b. Wenn du also die Reihenfolge falsch gewählt hast, ändere einfach das Vorzeichen. 🙃 -
Mehr Details und interessante Infos zum Kreuzprodukt findest du in unserem Artikel mit dem Titel "Das Kreuzprodukt von zwei Vektoren 🇺🇸".
-
Das Vektorprodukt hat viele Anwendungen in der Physik und im Ingenieurwesen — z. B. kannst du damit die Lorentzkraft 🇺🇸 bestimmen. Schau dir unseren Kreuzprodukt Rechner 🇺🇸 an, um mehr zu erfahren!
Vektormultiplikation — Skalarprodukt
Das Skalarprodukt wird mit einem Punkt ∙ als Malkreuz geschrieben und bezeichnet die Multiplikation zweier Vektoren zu einer Zahl . Für zwei Vektoren a und b ist ihr Skalarprodukt das Produkt ihrer Vektorbeträge |a| und |b| und dem Kosinus des Winkels θ zwischen ihnen:
a ∙ b = |a| × |b| × cos(θ).
-
In orthogonalen Koordinaten ist das Skalarprodukt die Summe der Produkte der entsprechenden Koordinaten deiner beiden Vektoren:
a ∙ b = ax × bx + ay × by + az × bz
Beispiel:
Das Skalarprodukt von
a = [2, 3, 4]undb = [1, -2, 3]ista - b = 2 × 1 + 3 × (-2) + 4 × 3 = 2 - 6 + 12 = 8. -
Wie du vielleicht schon aus der Formel entnommen hast, spielt die Reihenfolge hier keine Rolle:
a ∙ b = b ∙ a. -
Tipp: Wenn du das Skalarprodukt eines Vektors mit sich selbst berechnest, erhältst du einen quadrierten Vektorbetrag:
a ∙ a = |a|²! -
Weitere Informationen findest du in unserem Skalarprodukt Rechner 🇺🇸.
Vektor Projektion
Die Projektion von b auf a ist der Vektor, der die beste Annäherung an b unter den Vektoren ist, die man durch Strecken und Stauchen des Vektors a erhält. Um die Projektion zu finden, musst du also nur den richtigen Faktor für die Streckung und Stauchung kennen.
-
Formel:
Die Projektion von
baufaist der Vektoraskaliert um:a ∙ b / |a|².Beispiel:
Sei
a = [2, 3, 4]undb = [1, -2, 3]. Berechnen wir die Projektion vonbaufa. Zuerst müssen wir den Faktor für die Skalierung finden. Wir haben oben berechnet, dassa - b = 8und|a| = √29. Folglich ist die Projektion vonbaufa:8/29 ∙ [2, 3, 4] = [16/29, 24/29, 32/29] -
Um die Projektion von
baufagraphisch zu ermitteln, musst dubentlang der Achsen zerlegen, die vonaaufgespannt werden und senkrecht zu „a” stehen. Die Koordinate, die nebenaliegt, ist die Projektion vonbaufa. Du kannst dir das auch als den Schatten vorstellen, den der Vektorbauf den Vektorawerfen würde, wenn eine Lichtquelle über diesen Vektoren angebracht wäre:
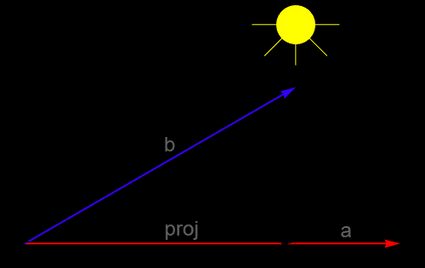
Mehr über die Projektion von Vektoren auf andere Vektoren erfährst du in unserem speziellen Vektorprojektion Rechner 🇺🇸.
FAQs
Was ist ein Vektor?
Ein Vektor ist ein mathematisches Objekt, das definiert ist durch:
- Einen Vektorbetrag; und
- Eine Richtung.
Sie unterscheiden sich wesentlich von skalaren Mengen: Letztere ändern sich nicht mit der Richtung.
Vektoren sind in der Physik weit verbreitet, wo sie Mengen wie Verschiebung und Geschwindigkeit beschreiben.
Wie berechne ich die Projektion eines Vektors auf einen anderen?
Wenn du die Vektoren a und b betrachtest, kannst du die Projektion von a auf b finden, indem du die nächsten Schritte befolgst:
- Berechne das Skalarprodukt zwischen
aundb:a ∙ b. - Berechne das Skalarprodukt von
bmit sich selbst:b ∙ b. - Berechne das Verhältnis zwischen den beiden Ergebnissen:
(a ∙ b)/(b ∙ b). - Multipliziere das Ergebnis (einen Skalar) mit dem Vektor
b:[(a ∙ b)/(b ∙ b)] × b.
Was ist das Skalarprodukt zweier Vektoren?
Das Skalarprodukt zweier Vektoren ist eine Operation, die darin besteht, das Produkt der Koordinaten zweier Vektoren dimensionsweise zu summieren.
Wenn du zwei Vektoren hast, a = (a₁, a₂, a₃, ..., an) und b = (b₁, b₂, b₃, ..., bn), befolge diese beiden Schritte, um das Skalarprodukt zu berechnen:
- Berechne das Produkt aus jedem Koordinatenpaar: a₁ × b₁, a₂ × b₂, usw.
- Addiere die Ergebnisse: (a₁ × b₁) + (a₂ × b₂).
Beachte, dass du nur das Skalarprodukt von Vektoren mit der gleichen Anzahl von Koordinaten berechnen kannst.
Was ist der Vektorbetrag eines Vektors mit den Koordinaten (3,1,4,1,5)?
Um den Vektorbetrag des Vektors mit den Koordinaten (3,1,4,1,5) zu berechnen, wende den verallgemeinerten Satz des Pythagoras auf alle Koordinaten an. Wenn der Vektor a = (a₁, a₂, a₃, ..., an) ist, finden wir den Vektorbetrag mit der Formel:
||a|| = √(a₁² + a₂² + a₃² + ... + an²)
Im Fall des Vektors (3,1,4,1,5) ist der Vektorbetrag:
√(3² + 1² + 4² + 1² + 5²) = √(9 + 1 + 16 + 1 + 25) = √(52) ≈ 7.21
