Vektoraddition Rechner

Willkommen bei Omni's Vektoraddition-Rechner, wo wir alles über die Addition von Vektoren im zweidimensionalen oder dreidimensionalen Raum lernen. Mit unserem Tool können wir die beiden Vektoren mit orthogonalen Koordinaten oder dem Vektorbetrag und dem Winkel angeben. Außerdem kann er Vielfache der Vektoren nehmen oder als Vektorsubtraktion-Rechner fungieren. Und für den Fall, dass du das Omni-Tool nicht zur Hand hast, geben wir die Formel für die Vektoraddition und beschreiben detailliert, wie man Vektoren mit der Parallelogrammregel addiert.

Du siehst lieber zu, als zu lesen? Sieh dir hier unser Lehrvideo über Vektorsubtraktion und -addition an:

Aus mathematischer Sicht ist ein Vektor eine geordnete Abfolge von Zahlen (ein Paar im zweidimensionalen, ein Dreifaches im dreidimensionalen Raum und mehr in höheren Dimensionen), und das ist alles, was er kann. Natürlich konnten Wissenschaftler es nicht dabei belassen, also haben sie diese Definition erweitert. Im Allgemeinen ist ein Vektor ein Element eines Vektorraums. Vektorräume können aus Abfolgen, Funktionen, Permutationen, Matrizen usw. bestehen. Zum Glück brauchen wir nichts davon in diesem Vektor-Additionsrechner.

Physiker hingegen betrachten Vektoren lieber als Pfeile (die ihre visuelle Darstellung sind), die Objekte beschreiben. Als solche stehen sie für Kräfte, die auf ein Objekt einwirken, sei es die Gravitation, die Bremskraft oder die magnetische Anziehungskraft. Die Richtung eines solchen Pfeils sagt uns, in welche Richtung die Kraft wirkt, während seine Länge die Größe der Kraft angibt.

Zum Glück sind beide Ansätze im Wesentlichen dasselbe, zumindest in unserem Fall und in diesem Vektor-Additionsrechner. Dennoch können wir Vektoren auf zwei Arten darstellen: mit orthogonalen Koordinaten oder mit dem Vektorbetrag und dem Winkel. Letzteres ist jedoch nur im zweidimensionalen Fall möglich, da es eigentlich den Polarkoordinaten entspricht.

Schauen wir uns ein Beispiel an. Ein Vektor v= (2,1) ist zweidimensional und sagt uns im Wesentlichen, dass „er zwei Schritte entlang der X-Achse und einen Schritt entlang der Y-Achse geht.” Beachte, dass positive Koordinaten bedeuten, dass man sich nach rechts und nach oben bewegt (entlang der horizontalen bzw. vertikalen Achse), während negative Koordinaten die entgegengesetzte Richtung anzeigen. Wenn wir eine dritte Koordinate hinzufügen, z. B. w= (2,1,5), befinden wir uns im dreidimensionalen Raum und die zusätzliche 5 entspricht der Bewegung entlang der Z-Achse.

Alternativ können wir den zweidimensionalen Vektor v auch mit seinem Vektorbetrag m und seiner Richtung θ darstellen. Ersteres ist einfach die Länge des Vektors. Letzteres ist der Winkel, den der Vektor gegen den Uhrzeigersinn mit der positiven Hälfte der horizontalen Achse einschließt, wenn er in der Ebene mit dem Startpunkt in (0,0) gezeichnet wird.

Das bedeutet insbesondere, dass m nicht negativ sein darf, während θ zwischen 0 und 360 Grad (oder zwischen 0 und 2π im Bogenmaß) liegen sollte. Dieser Rechner zum Addieren von Vektoren akzeptiert aber auch andere Winkelwerte, und zwar nach denselben Regeln, die für trigonometrische Funktionen und ihre Argumente gelten.

An dieser Stelle sei erwähnt, dass es ein Äquivalent zu den Polarkoordinaten (Vektorbetrag und Richtung) im dreidimensionalen Raum gibt, die sogenannten Kugelkoordinaten. Sie sind jedoch unübersichtlich und in der Praxis weit weniger verbreitet, weshalb wir sie in unserem Vektor-Additionsrechner auslassen. Trotzdem kannst du in unserem Rechner für Kugelkoordinaten 🇺🇸 mehr über sie erfahren.

So, jetzt kennen wir das Objekt, mit dem wir es zu tun haben, ganz gut. Es ist an der Zeit zu sehen, wie man Vektoren addiert.

Vektoren zu addieren ist einfach, besonders bei orthogonalen Koordinaten. Um genau zu sein, addieren wir nur die Zahlen in den Koordinaten. Das bedeutet, dass die Formel für die Addition von Vektoren im zweidimensionalen Raum wie folgt lautet:

(a,b) + (d,e) = (a + d, b + e),

und die dreidimensionale Formel lautet

(a,b,c) + (d,e,f) = (a + d, b + e, c + f).

Das ist alles, ohne weitere Bedingungen. Es ist schön, zur Abwechslung mal eine einfache Formel zu haben, nicht wahr?

Wenn wir im zweidimensionalen Raum den Vektorbetrag und die Richtung verwenden, wird die Sache etwas komplizierter. Leider können wir in diesem Fall nicht einfach die Werte der beiden Vektoren addieren, wie wir es bei kartesischen Koordinaten getan haben. Warum das so ist, wird im nächsten Abschnitt mithilfe des Parallelogrammgesetzes anschaulich erklärt.

Möchtest du die Vektoren nicht zeichnen, ist der beste Weg, ihre Summe in dieser Form zu ermitteln. Finde ihre Darstellung in orthogonalen Koordinaten und verwende die Vektor-Additionsformel vom Anfang dieses Abschnitts.

Natürlich ist es hilfreich, dass der Übergang zwischen den Formen relativ einfach ist. Um genau zu sein, wenn ein Vektor v den Vektorbetrag m und die Richtung θ hat, dann ist v= (x,y) in kartesischen Koordinaten:

x = m × cos(θ) und y = m × sin(θ),

wobei cos und sin die trigonometrischen Funktionen Kosinus bzw. Sinus sind (mehr darüber erfährst du im Trigonometrische Funktionen Rechner 🇺🇸). Der Vollständigkeit halber erwähnen wir auch die Übergangsformel von polaren Koordinaten zu orthogonalen Koordinaten:

m = √(x² + y²) und θ = arccos(x / m),

wobei arccos die inverse Kosinusfunktion ist (mehr dazu in unserem arccos-Rechner 🇺🇸).

Bevor wir dir die Parallelogrammregel zeigen, schauen wir uns noch ein paar Zusatzfunktionen des Vektor-Additionsrechners an.

1. Vektorsubtraktion-Rechner
   Wir geben ihm einen so ausgefallenen Namen, aber es läuft auf eine supereinfache Änderung hinaus. Um genau zu sein, möchtest du statt Vektoren zu addieren, ihre Differenz berechnen. Die Regeln sind dieselben wie vorher: Wir subtrahieren die Vektoren koordinatenweise. Um diese Option zu nutzen, wählst du einfach Subtraktion unter Operation im Tool und das Ding verwandelt sich in einen Vektor-Subtraktions-Rechner.

2. Addieren von Vektoren mit Vielfachen
   Es kann vorkommen, dass du einen Vektor nicht nur einmal, sondern mehrere Male addieren möchtest. Zum Beispiel würde v+ 4 ×w bedeuten, vier Kopien von w zu v zu addieren. Anstatt den Vektor-Additionsrechner viermal zu benutzen, um das Ergebnis zu ermitteln, kannst du ohne Vielfache in mit Vielfachen ändern und die Werte von α und β eingeben. Natürlich kannst du diese Option auch mit Punkt 1. kombinieren und hast dann einen Vektor-Subtraktionsrechner mit Multiplikatoren.

Im ersten Abschnitt haben wir erwähnt, dass wir Vektoren als Pfeile darstellen. Bisher haben wir uns nur algebraisch mit ihnen beschäftigt, wie in der Formel für die Vektoraddition. Jetzt ist es an der Zeit, zurück zur Zeichnung zu kommen — zum Zeichnen von Parallelogrammen.

Im Grunde genommen bedeutet das Addieren von Vektoren, dass man sich erst entlang des einen und dann entlang des anderen Vektors bewegt. Das heißt, wenn wir einen Vektor als Pfeil zeichnen, dann bedeutet das eine Verschiebung entlang des Pfeils, dass wir uns (als Punkt) von seinem Startpunkt zum Endpunkt bewegen. Wenn wir uns von dort aus mit dem zweiten Pfeil bewegen möchten, können wir ihn einfach vom ersten Endpunkt aus zeichnen, und der Ort, auf den der Pfeil zeigt, wäre unser Ergebnis.

Oben haben wir die Grundidee des visuellen Addierens von Vektoren beschrieben, auf der auch die Parallelogrammregel beruht. Es ist nur eine schickere Art, es auszudrücken, denn: Die Summe zweier Vektoren ist die Diagonale eines Parallelogramms, dessen Seiten die beiden addierten Vektoren sind, wenn sie aus demselben Punkt heraus gezeichnet werden.

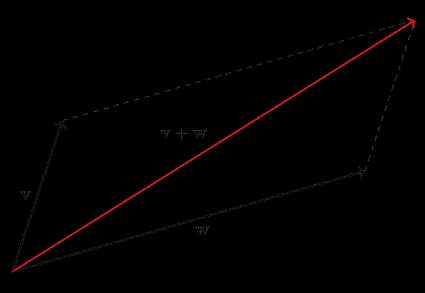
In der Abbildung können wir uns von dem Scheitelpunkt, an dem v und w beginnen, zum gegenüberliegenden Scheitelpunkt bewegen, indem wir uns zuerst entlang v und dann entlang w bewegen, oder umgekehrt (der zweite Schritt wird dann durch eine gestrichelte Gerade eingezeichnet). Das ist dasselbe, was wir am Anfang dieses Abschnitts gemacht haben. Beachte auch, dass die Reihenfolge der Verschiebung nicht ausschlaggebend ist, da die Addition kommutativ ist.

Und damit schließen wir den theoretischen Teil für ab. Lass uns all dieses Wissen anwenden und sehen, wie der Vektor-Additionsrechner in der Praxis funktioniert.

Angenommen, wir möchten die Summe eines Vektors v= (-3,2,8) und drei Vielfache von w= (2,2,-4) finden. Sehen wir uns an, wie wir mit dem Vektoraddition-Rechner die Lösung finden können.

Beachte zunächst, dass wir Vektoren mit drei (orthogonalen) Koordinaten addieren; sie sind also dreidimensional. Deshalb müssen wir unter „3D” „Vektoren” und unter „Operation” „Addition” auswählen. Das zeigt uns zwei Abschnitte für die Koordinaten, jeder mit drei variablen Feldern, die mit x, y und z gekennzeichnet sind und dem ersten, zweiten bzw. dritten Koordinaten entsprechen. In dem Abschnitt, der v = (-3,2,8) beschreibt, geben wir also ein:

x = -3, y = 2, z = 8,

und in den Abschnitt von w= (2,2,-4), schreiben wir:

x = 2, y = 2, z = -4.

Sobald wir den letzten Wert eingegeben haben, sehen wir v + w im Abschnitt „Ergebnis”. Aber das ist nicht wirklich das, was wir brauchen, oder? Wir möchten drei Vielfache von w hinzufügen und nicht nur eine.

Deshalb wählen wir oben im Rechner die Option „mit Vielfachen”, die α ×v+ β ×w berechnet, anstatt nur v + w. Beachte, dass wir dort bereits α = 1 und β = 1 als Standard eingegeben haben. Für unser Problem ändern wir sie in:

α = 1, β = 3,

was uns die endgültige Lösung liefert. Doch bevor wir sie verraten, benutzen wir die Formel für die Vektoraddition und ermitteln die Summe selbst.

Beachte, dass die Addition von drei Vielfachen eines Vektors gleichbedeutend ist mit der Dreifachaddition seiner Koordinaten. Deshalb,

v+ 3 ×w= (-3,2,8) + 3 × (2,2,-4) = (-3 + 3 × 2, 2 + 3 × 2, 8 + 3 × (-4)) = (3,8,-4).

Voilà! Das war eine Reihe an Berechnungen, aber kannst du dir vorstellen, dass du das alles mit ein paar schrecklich komplizierten Eingaben machen möchtest? Gut, dass wir den Vektor-Additionsrechner von Omni haben, der uns Zeit und Ärger erspart.

Die Summe der Vektoren x = (x₁, x₂, ..., x_k) und y = (y₁, y₂, ..., y_k) ist gleich:

x + y = (x₁ + y₁, x₂ + y₂, ..., x_k + y_k).

Das heißt, wir führen die Addition koordinatenweise durch. Für zweidimensionale Vektoren erhalten wir:

(x₁, x₂) + (y₁, y₂) = (x₁ + y₁, x₂ + y₂).

Um eine Vektoraddition durchzuführen:

1. Addiere die Koordinaten an der ersten Position: 2 + 1 = 3.
2. Addiere die Koordinaten an der zweiten Position: 1 + 0 = 1.
3. Schreibe die Ergebnisse von Schritt 1 und 2 auf: (3,1).
4. Das war's! Du hast soeben erfolgreich die Vektoraddition durchgeführt!

Die Formel für den Vektorbetrag von x + y = (x₁ + y₁, x₂ + y₂) lautet:

|x + y| = √[(x₁ + y)²+(x₂ + y₂)²].

Wie du sicher bemerkt hast, wird hier der Satz des Pythagoras verwendet!

Die Formel für den Richtungswinkel der Summe der Vektoren x + y = (x₁ + y₁, x₂ + y₂) lautet wie folgt:

θ = arctan((x₂ + y₂)/(x₁ + y₁)),

wobei arctan die Funktion des Arkustangens (inverser Tangens) bezeichnet.