Polarkoordinaten Rechner
Inhalt
Kartesische Koordinaten und PolarkoordinatenWie rechne ich kartesische Koordinaten in Polarkoordinaten um?Wie rechne ich Polarkoordinaten in kartesische Koordinaten um?FAQsDieser Polarkoordinaten-Rechner ist ein praktisches Werkzeug, mit dem du kartesische Koordinaten in Polarkoordinaten umrechnen kannst und umgekehrt. Er ist nur im zweidimensionalen Raum anwendbar – für dreidimensionale Koordinaten kannst du unseren Zylinderkoordinaten Rechner 🇺🇸 verwenden. In diesem Artikel findest du eine kurze Erklärung der beiden Koordinatenarten und Formeln für eine schnelle Umrechnung.
Kartesische Koordinaten und Polarkoordinaten
Wie du wahrscheinlich weißt, verwenden wir Koordinaten, um die Position eines Punktes im Raum eindeutig zu beschreiben. Für den Moment beschränken wir uns auf einen zweidimensionalen Raum. Das bedeutet, dass wir nur zwei Dimensionen haben: Höhe und Breite (keine Tiefe), genau wie auf einem Blatt Papier.
Das kartesische Koordinatensystem entsteht durch das Einzeichnen zweier senkrechter Geraden. Der Punkt, an dem sie sich treffen, wird als Ursprung des Koordinatensystems bezeichnet. Die Koordinaten eines beliebigen Punktes im Raum sind die Entfernungen zwischen diesem Punkt und den beiden Geraden, die mit x-Achse und y-Achse bezeichnet werden. Mehr über die Berechnung der Entfernung zwischen zwei Punkten erfährst du mit unserem Entfernungsrechner.
Im Polarkoordinatensystem gibt es dagegen keine senkrechten Geraden. Der Ursprung des Polarsystems ist ein Punkt, der Pol genannt wird. Ein beliebiger Strahl, der von diesem Punkt ausgeht, wird als Polarachse bezeichnet. Um die Koordinaten eines bestimmten Punktes zu bestimmen, musst du zunächst eine Gerade ziehen, die den Punkt mit dem Pol verbindet. Die Koordinaten des Punktes sind dann die Länge dieser Gerade und der Winkel θ, den sie mit der Polarachse bildet.
Unser Polarkoordinaten-Rechner kann in beide Richtungen zwischen kartesischen und polaren Koordinaten umrechnen. Er geht davon aus, dass sich der Ursprung des kartesischen Systems mit dem Pol des Polarsystems überschneidet.
Wie rechne ich kartesische Koordinaten in Polarkoordinaten um?
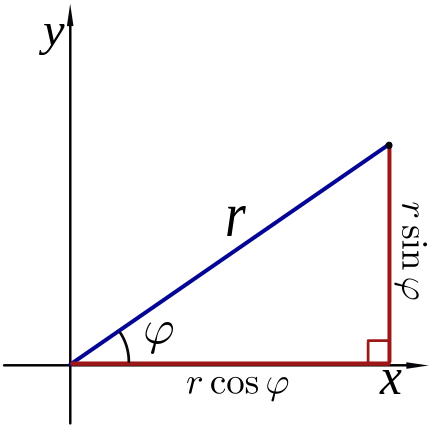
Wenn du die kartesischen Koordinaten (x,y) eines Punktes kennst und sie als Polarkoordinaten (r,θ) ausdrücken möchtest, benutze die folgenden Formeln:
r = √(x² + y²) und θ = arctan(y/x).
Denke daran, dass für die Polarkoordinaten die folgenden Bedingungen gelten:
rmuss größer oder gleich 0 sein; undθmuss innerhalb des Bereichs (-π, π] liegen.
Wie rechne ich Polarkoordinaten in kartesische Koordinaten um?
Um von den Polarkoordinaten (r,θ) eines Punktes zu den kartesischen Koordinaten (x,y) zu gelangen, benutze einfach die folgenden Gleichungen:
x = r∙× cos θ und y = r ∙ sin θ.
Du kannst feststellen, dass der Wert y/x die Steigung der Geraden ist, die den Pol und den beliebigen Punkt verbindet.
🙋 Vielleicht interessieren dich auch unser Kugelkoordinaten Rechner 🇺🇸 und Steigung Rechner.
Können alle kartesischen Koordinaten in Polarkoordinaten umgewandelt werden?
Ja, jeder Punkt (x,y) in der kartesischen Ebene kann in Polarkoordinaten (r,θ) umgewandelt werden.
Wie lautet die Polarform des kartesischen Punktes (0,0)?
Die polare Form von (0,0) ist nicht eindeutig, denn jeder polare Punkt (0,ϕ) repräsentiert den kartesischen Punkt (0,0). Aus Konvention wählen wir jedoch oft (0,0) als die polaren Koordinaten des kartesischen Punktes (0,0).
Was ist die Polarkoordinate (2,π) in kartesischen Koordinaten?
So konvertierst du von polare in kartesische Koordinaten:
- Erinnere dich an die Umrechnungsformeln
x = r ∙ cos θundy = r ∙ sin θ. - Berechne
sin(π) = 0undcos(π) = -1. - Wir erhalten also
x = 2 ∙ (-1)undy = 2 ∙ 0 - Wir kommen zu den kartesischen Koordinaten
(-2,0).