Zuletzt aktualisiert: 14. Nov 2024

Steigung Rechner

Q: Wie findet man die Steigung einer Geradengleichung?

Die Methode zur Ermittlung der Steigung aus einer Geradengleichung hängt von der Form der Gleichung ab, die du vor dir hast. Wenn die Gleichung in der Normalform y = mx + c vorliegt, dann ist die Steigung (oder das Gefälle) einfach m . Wenn du eine andere Form von Gleichung hast, versuche, die Gleichung in die Normalform umzustellen. Um die Steigung anderer Polynome zu finden, musst du die Funktion nach x differenzieren.

Q: Wie berechnet man die Steigung eines Hügels?

Verwende eine Karte, um die Entfernung zwischen dem oberen und unteren Ende des Hügels in Luftlinie zu bestimmen. Verwende dieselbe Karte oder GPS, um die Höhe zwischen dem oberen und unteren Ende des Hügels zu bestimmen. Achte darauf, dass die Punkte, von denen aus du misst, dieselben sind wie in Schritt 1. Rechne beide Messungen in dieselben Einheiten um. Dividiere die Höhendifferenz durch die Entfernung zwischen den beiden Punkten. Diese Zahl ist die lineare Steigung des Hügels. Ist die Steigung nicht linear, wiederhole die Schritte, an den Stellen, an der sich die Steigung merklich verändert.

Q: Was sind Alltagsbeispiele für die Steigung?

Steigungen (oder Gefälle) begegnen dir überall im Alltag . Es gibt einige offensichtliche physikalische Beispiele — jeder Hügel hat eine Steigung, und je steiler der Hügel ist, desto größer ist seine Steigung . Das kann nützlich sein, wenn du dir eine Karte ansiehst und den besten Berg zum Radfahren finden möchtest. Wahrscheinlich schläfst du auch unter einem Gefälle, also einem Dach . Die Neigung eines Daches hängt von der Bauart ab und davon, wo du wohnst. Was noch viel wichtiger ist: Wenn du beobachtet hast, wie sich etwas über einen Zeitraum verändert, wirst du am Ende ein Diagramm mit einer Steigung aufgezeichnet haben .

Erstellt von Mateusz Mucha und Julia Żuławińska

Überprüft von Bogna Szyk und Jack Bowater

Übersetzt von Luise Schwenke

Luise Schwenke

Luise works as a German translator and Calculatorian at Omni. She holds a degree in Food Engineering from the University of Sciences - Neubrandenburg, Germany, and specialized her career in biotechnology. She worked in human genetic diagnostics, developing and producing pharmaceutical products for clinical phase 2 and 3 studies. She is always hungry for new fields to learn about that allow her to combine her creative and analytical thinking. Currently, she is getting her hands on coding, focusing on data science and big data. Luise spent an academic year in Brazil and loves traveling the world to experience and learn from different cultures. See full profile

Check our editorial policy

und Julia Kopczyńska, promovierend

Julia Kopczyńska

PhD candidate, Polish Academy of Sciences

LinkedInResearch Gate

A microbiologist with a low-key addiction to coffee. Since her Bachelor’s, she has focused on the gut microbiome and its role in human health. Now she hopes to find the golden bacteria to improve gut health in her Ph.D. project. She enjoys scientific writing and digging really deep into a topic. She has been living in 5 different countries and loves to travel to new places. In her free time, she likes to be active by playing volleyball, biking, and going for long walks. See full profile

Check our editorial policy

Neu

Inhalt

So benutzt du den Rechner für die Steigung Formel für die Steigung Berechnung der Steigung Verwandte Themen Die Entstehung des Steigung Rechners FAQs

Der Steigung-Rechner bestimmt die Steilheit der Geraden zwischen zwei Punkten im kartesischen Koordinatensystem. Die Steigung ist im Grunde die Neigung einer Geraden und kann einen positiven, negativen, Null- oder undefinierten Wert haben. Bevor du den Rechner verwendest, ist es hilfreich, wenn du weißt, wie die Steigung mithilfe der Steigungsformel bestimmt wird. Um die Gleichung einer Geraden für zwei beliebige Punkte zu finden, durch welche die Gerade verläuft, kannst du unseren Hauptform einer Geradengleichung Rechner verwenden.

So benutzt du den Rechner für die Steigung

Um es dir einfacher zu machen, erklären wir dir hier, wie du diesen Rechner verwendest, und zeigen dir ein Rechenbeispiel. Um die Steigung einer Geraden zu berechnen, musst du zwei beliebige Punkte auf der Geraden kennen:

Gib die x- und y-Koordinaten des ersten Punktes auf der Geraden ein.
Gib die x- und y-Koordinaten des zweiten Punktes auf der Geraden ein.
Wir erhalten sofort die Steigung der Geraden. Die Magie endet hier jedoch nicht, denn es werden noch eine Vielzahl weiterer Ergebnisse präsentiert:
- Die Gleichung deiner Funktion (entspricht der Gleichung der Geraden).
- Den y-Schnittpunkt der Geraden.
- Den Winkel, den die Gerade mit der x-Achse bildet (gegen den Uhrzeigersinn gemessen).
- Die Steigung in Prozent (Prozentgrad).
- Die Entfernung zwischen den beiden Punkten.

Ein Beispiel: Angenommen, du hast eine Gerade, die durch die Punkte (1, 5) und (7, 6) verläuft. Gib die x- und y-Koordinaten des ersten Punktes ein, gefolgt von den x- und y-Koordinaten des zweiten Punktes. Wir erfahren sofort, dass die Steigung der Geraden 0,166667 beträgt. Wir erhalten auch die Gleichung der Geraden: y = 0,16667x + 4,83333.

Du kannst diesen Rechner auch umgekehrt benutzen, um eine fehlende x- oder y-Koordinate finden! Betrachte zum Beispiel die Gerade, die durch den Punkt (9, 12) geht und eine Steigung von 12 % hat. Um den Punkt zu finden, an dem die Gerade die y-Achse schneidet (d. h. x = 0), gibst du 12% in Prozentgrad (9, 12) als Koordinate des ersten Punktes ein und x₂ = 0. Der Rechner sagt uns sofort, dass y₂ = 10,92 ist.

Die Steigung einer Geraden wird in der Geometrie und in der Infinitesimalrechnung häufig verwendet. Der folgende Artikel ist eine hervorragende Einführung in die Grundlagen dieses Themas und wir empfehlen dir, ihn zu lesen.

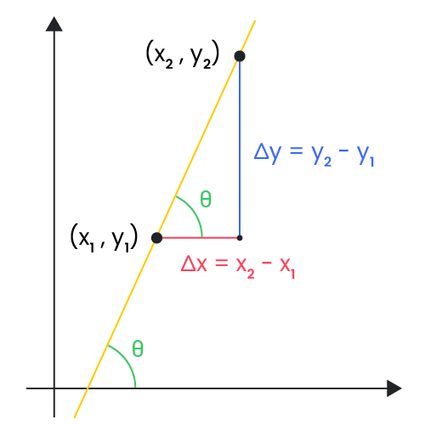
Formel für die Steigung

\mathrm{Steigung} = \frac{y_2 - y_1}{x_2 - x_1}

Du kannst die Steigung einer Geraden mit kleinen, ganzzahligen Koordinaten leicht handschriftlich berechnen. Je größer die Werte werden oder falls du mit Dezimalzahlen rechnest, desto komplizierter wird die Berechnung und desto nützlicher ist dieser Steigung-Rechner.

Beachte, dass auch eine horizontale Gerade eine Steigung hat, sie beträgt allerdings 0, da die Punkte die gleichen y-Koordinaten haben. Dies führt zu einer Null im Zähler der Steigungsformel. Eine vertikale Gerade hingegen hat eine undefinierte Steigung, da die x-Koordinaten immer gleich sind. Wenn du dies in die Formel einsetzt, kommt es zum Divisionsfehler, da nicht durch null geteilt werden kann.

Berechnung der Steigung

Bestimme die Koordinaten $(x_1, y_1)$ und $(x_2, y_2)$ , die die Gerade verbinden. Wir können nun mit der obigen Formel beispielsweise die Steigung der Geraden, die durch die Punkte $(3, 8)$ und $(-2, 10)$ verläuft, berechnen.
Setze die Werte in die Formel ein. So erhalten wir $(10 - 8)/(-2 - 3)$ .
Subtrahiere die Werte in den Klammern, um $2/(-5)$ zu erhalten.
Vereinfache den Bruch, um die Steigung von $-2/5$ zu erhalten.
Überprüfe dein Ergebnis mithilfe des Steigung-Rechners.

Um die Steigung einer Geraden zu bestimmen, brauchen wir zwei Koordinatenpunkte, die auf der Geraden liegen. Da die Steigung die Veränderung der y-Koordinate, geteilt durch die Veränderung der x-Koordinate ist, kannst du zwei beliebige Koordinatenpunkte auswählen. Die Berechnungen zur Ermittlung der Steigung sind einfach und beinhalten nichts weiter als einfache Subtraktion und Division.

🙋 Um die Steigung nichtlinearer Funktionen zu ermitteln, kannst du den Rechner für die mittlere Änderungsrate verwenden.

Die Entstehung des Steigung Rechners

Der Steigung-Rechner ist einer der ältesten bei Omni Calculator. Dieser Rechner wurde von unseren erfahrenen Experten Mateusz und Julia entwickelt, die sich darauf spezialisiert haben, präzise wissenschaftliche Werkzeuge zu erstellen. Die Idee für diesen Rechner entstand, als die beiden sich mit Datenanalysen und Trends beschäftigten und erkannten, wie ein Rechner für Steigungen ihre Arbeit erleichtern würde. Auch heute noch kannst du die beiden gelegentlich dabei beobachten, wie sie dieses Tool für zuverlässige Berechnungen nutzen.

Wir legen besonderen Wert auf die Qualität unserer Inhalte, damit sie so genau und verlässlich wie möglich sind. Jedes Tool wird von einem geschulten Experten getestet und anschließend von einem Muttersprachler Korrektur gelesen. Mehr über unsere Standards erfährst du in unseren Redaktionsrichtlinien.

FAQs

Wie findet man die Steigung einer Geradengleichung?

Die Methode zur Ermittlung der Steigung aus einer Geradengleichung hängt von der Form der Gleichung ab, die du vor dir hast. Wenn die Gleichung in der Normalform y = mx + c vorliegt, dann ist die Steigung (oder das Gefälle) einfach m. Wenn du eine andere Form von Gleichung hast, versuche, die Gleichung in die Normalform umzustellen. Um die Steigung anderer Polynome zu finden, musst du die Funktion nach x differenzieren.

Wie berechnet man die Steigung eines Hügels?

Verwende eine Karte, um die Entfernung zwischen dem oberen und unteren Ende des Hügels in Luftlinie zu bestimmen.
Verwende dieselbe Karte oder GPS, um die Höhe zwischen dem oberen und unteren Ende des Hügels zu bestimmen. Achte darauf, dass die Punkte, von denen aus du misst, dieselben sind wie in Schritt 1.
Rechne beide Messungen in dieselben Einheiten um.
Dividiere die Höhendifferenz durch die Entfernung zwischen den beiden Punkten.
Diese Zahl ist die lineare Steigung des Hügels. Ist die Steigung nicht linear, wiederhole die Schritte, an den Stellen, an der sich die Steigung merklich verändert.

Wie berechnet man die Länge eines Abhangs?

Miss die Differenz zwischen dem oberen und unteren Ende des Abhangs in Bezug auf die x- und y-Achse.
Wenn du nur die Veränderung von x messen kannst, multipliziere diesen Wert mit der Steigung, um die Veränderung auf der y-Achse zu ermitteln.
Achte darauf, dass die Einheiten für beide Werte gleich sind.
Verwende den Satz des Pythagoras, um die Länge der Steigung zu bestimmen. Quadriere sowohl die Änderung von x als auch die Änderung von y.
Addiere die beiden Werte zusammen.
Finde die Quadratwurzel aus der Summe.
Dieser neue Wert ist die Länge der Steigung.

Was ist ein Anstieg von 20%?

Ein Anstieg von 20% bedeutet, dass die Strecke pro 20 horizontal zurückgelegte Einheiten um 1 Einheit zunimmt. Eine Strecke, die 200 Meter lang und 10 Meter hoch ist, hätte also eine Neigung von 20%. Ein Anstieg von 20% entspricht einer Steigung von 1/20 und bildet mit der x-Achse einen Winkel von 2,86°.

Wie findet man die Steigung einer Kurve?

Da sich die Steigung einer Kurve an jedem Punkt ändert, kannst du sie ermitteln, indem du die Gleichung nach x** differenzierst und in der resultierenden Gleichung für x den Punkt einsetzt, an dem du die Steigung ermitteln möchtest.

Ist die Änderungsrate dasselbe wie die Steigung?

Die Änderungsrate eines Graphen ist auch seine Steigung bzw. Neigung. Die Änderungsrate lässt sich ermitteln, indem man die Änderung in y-Richtung (vertikal) durch die Änderung in x-Richtung (horizontal) teilt. Achte darauf, dass beide Zahlen in denselben Einheiten vorliegen. Die Änderungsrate ist besonders nützlich, wenn du z. B. die Zukunft eines Wertes vorhersagen oder den vorherigen Wert bestimmen möchtest, da sich, wenn du die x-Variable änderst, der entsprechende y-Wert anpasst (und umgekehrt).

Was sind Alltagsbeispiele für die Steigung?

Steigungen (oder Gefälle) begegnen dir überall im Alltag. Es gibt einige offensichtliche physikalische Beispiele — jeder Hügel hat eine Steigung, und je steiler der Hügel ist, desto größer ist seine Steigung. Das kann nützlich sein, wenn du dir eine Karte ansiehst und den besten Berg zum Radfahren finden möchtest. Wahrscheinlich schläfst du auch unter einem Gefälle, also einem Dach. Die Neigung eines Daches hängt von der Bauart ab und davon, wo du wohnst. Was noch viel wichtiger ist: Wenn du beobachtet hast, wie sich etwas über einen Zeitraum verändert, wirst du am Ende ein Diagramm mit einer Steigung aufgezeichnet haben.

Was ist eine 10%-ige Steigung?

Eine Steigung von 10% steigt um 1 Einheit pro 10 horizontal verlaufende Einheiten (10%). Ein Dach mit einem Gefälle von 10%, das 20 m breit ist, ist zum Beispiel 2 m hoch. Das entspricht einer Steigung von 1/10. Zwischen der Gerade und der x-Achse bildet sich ein Winkel von 5,71°.

Wie berechnet man die Fläche unter einer Steigung?

Um den Flächeninhalt einer Steigung zu ermitteln, die durch die Gleichung y = mx + c gegeben ist, gehst du folgendermaßen vor:

Bestimme die untere und obere Grenze von x, um einen Wert für Δx zu erhalten.
Multipliziere Δx mit der Steigung (m), um Δy zu erhalten.
Multipliziere Δx mit Δy.
Dividiere durch 2 um den Flächeninhalt unter der Steigung zu erhalten.

Wie steil ist eine Steigung von 5%?

Eine Steigung von 5% steigt für jede Erhöhung um 5 Einheiten horizontal um 1 Einheit an. Die Gradzahl zwischen einer Steigung von 5% und der x-Achse beträgt 11,3°. Du kannst diese Steigung berechnen, indem du die Veränderung in y-Richtung durch die Veränderung in x-Richtung teilst, und dann den inversen Tangens (Arkustangens) der Steigung findest.