Hauptform einer Geradengleichung Rechner

Mit dem Hauptform-einer-Geradengleichung-Rechner lernst du, wie du die Gleichung einer Geraden aus zwei beliebigen Punkten, durch die diese Geraden verläuft, bestimmen kannst. Er hilft dir, die Steigung und den y-Achsenabschnitt, sowie den x-Achsenabschnitt mithilfe der Geradengleichung zu finden. Lies weiter, um zu erfahren, wie die Hauptform einer Geradengleichung aussieht, wie du die Gleichung einer Geraden findest und welche Bedeutung diese Formel im echten Leben hat.

Jede Linie auf einer ebenen Fläche kann mathematisch als eine Beziehung zwischen den vertikalen (y-Achse) und horizontalen (x-Achse) Positionen der einzelnen Punkte, die diese Linie bilden, beschrieben werden. Diese Beziehung kann als y = [ein Ausdruck mit x] geschrieben werden. Was genau in dem Ausdruck mit x steht, bestimmt, um welche Art von Linie es sich handelt. y = x² + x ist z. B. eine Parabel, auch quadratische Funktion genannt. Andererseits entspricht y = mx + b (wobei m und b für beliebige reelle Zahlen stehen) einer Geraden.

In diesem Hauptform-einer-Geradengleichung-Rechner werden wir uns nur auf die gerade Linie konzentrieren. Du kannst unseren Rechner für die mittlere Änderungsrate benutzen, um die Beziehung zwischen den Variablen nicht-linearer Funktionen zu ermitteln.

Lineare Gleichungen oder Geradengleichungen kannst du schnell daran erkennen, dass sie keine Terme mit Exponenten enthalten. (Du findest zum Beispiel ein x oder ein y, aber niemals ein x².) Jede lineare Gleichung beschreibt eine Gerade und kann in der Hauptform dargestellt werden.

Wie wir bereits gesehen haben, kannst du die Gleichung einer beliebigen Geraden in der Form y = mx + b schreiben. Das ist die Hauptform. Du kannst diese Werte später für die lineare Interpolation verwenden.

Der Begriff Steigung ist die Neigung oder der Gradient einer Linie und wird in der Formel durch m dargestellt. Sie gibt an, wie sehr sich y bei einer festen Änderung von x verändert. Wenn sie positiv ist, steigen die Werte von y, wenn x steigt. Wenn sie negativ ist, nimmt y mit steigendem x ab. Mehr darüber kannst du in der Beschreibung unseres Steigung Rechners lesen.

Der y-Achsenabschnitt ist der Wert von y, an dem die Gerade die y-Achse schneidet und wird in der Formel durch b dargestellt. Um diesen Schnittpunkt zu finden, musst du x = 0 in die lineare Gleichung einsetzen. Du wirst später sehen, warum der y-Achsenabschnitt ein wichtiger Parameter in linearen Gleichungen ist. Du wirst auch etwas über die physikalische Bedeutung seines Wertes in bestimmten realen Beispielen erfahren.

Möchtest du immer noch wissen, wie du die Hauptform einer linearen Gleichung finden kannst? Wir nehmen an, dass du zwei Punkte kennst, durch die die Gerade verläuft. Der erste Punkt hat die Koordinaten (x₁, y₁) und der zweite Punkt (x₂, y₂). Deine Unbekannten sind die Steigung m und der y-Achsenabschnitt b.

Setze zunächst die Koordinaten der beiden Punkte in die Hauptform ein:

(1) y₁ = mx₁ + b

(2) y₂ = mx₂ + b

Ziehe dann die erste Gleichung von der zweiten ab:

y₂ - y₁ = m(x₂ - x₁)

Teile schließlich beide Seiten der Gleichung durch (x₂ - x₁), um die Steigung zu ermitteln:

m = (y₂ - y₁)/(x₂ - x₁)

Wenn du die Steigung gefunden hast, kannst du sie in die erste oder zweite Gleichung einsetzen, um den y-Achsenabschnitt zu finden:

y₁ = x₁(y₂ - y₁)/(x₂ - x₁) + b

b = y₁ - x₁(y₂ - y₁)/(x₂ - x₁)

Mit diesem Hauptform-einer-Geradengleichung-Rechner kannst du die Gleichung einer Geraden in der Hauptform finden. Alles, was du tun musst, ist, zwei Punkte anzugeben, durch die die Linie verläuft. Befolge das unten beschriebene Verfahren.

1. Schreibe die Koordinaten des ersten Punktes auf. Nehmen wir an, es ist ein Punkt mit x₁ = 1 und y₁ = 1.

2. Schreibe auch die Koordinaten des zweiten Punktes auf. Nehmen wir einen Punkt mit x₂ = 2 und y₂ = 3.

3. Benutze die Hauptform, um die Steigung zu ermitteln:

   m = (y₂ - y₁)/(x₂ - x₁) = (3-1)/(2-1) = 2/1 = 2.

4. Berechne den y-Achsenabschnitt. Du kannst hier auch x₂ und y₂ anstelle von x₁ und y₁ verwenden.

   b = y₁ - m ∙ x₁ = 1 - 2∙1 = -1

5. Setze alle diese Werte zusammen, um die Hauptform einer linearen Gleichung zu erhalten:

   y = 2x - 1.

6. Du kannst auch den Abstandsrechner verwenden, um den Abstand zwischen zwei Punkten zu ermitteln.

Es ist immer möglich, den x-Achsenabschnitt einer Geraden zu finden. Das ist der Wert von x, bei dem die Gerade die x-Achse schneidet (also der Wert von x, für den y gleich 0 ist). Du kannst ihn auf die folgende Weise berechnen:

0 = mx + b

x = -b/m

Wie wir sehen können, ist die einzige Bedingung, dass die Steigung m ungleich null sein muss.

Analog kannst du den y-Achsenschnittpunkt berechnen, indem du x = 0 setzt und die Gleichung für y löst.

Unser Hauptform-einer-Geradengleichung-Rechner zeigt dir sowohl die Werte des x- als auch des y-Achsenabschnitts an. Wenn du noch mehr darüber erfahren möchtest, empfehlen wir dir unseren x- und y-Achsenabschnitt Rechner 🇺🇸.

Wir haben bereits gesehen, was die Hauptform ist. Um zu verstehen, warum sie so nützlich ist, schauen wir uns nun einige Anwendungen aus dem Alltag an. Wir beginnen mit einfachen Beispielen aus der Physik, damit du eine Intuition dafür bekommst, was der y-Achsenabschnitt und der x-Achsenabschnitt bedeuten.

Stell dir ein Auto vor, dass mit einer festen Geschwindigkeit auf dich zukommt. Seine Bewegung kann als die Entfernung des Autos zu dir in Abhängigkeit von der Zeit dargestellt werden (wie oben). Das bedeutet, dass die x-Achse die vergangene Zeit und die y-Achse die Entfernung zum Auto darstellt. Du kannst dir sogar vorstellen, dass sich das Auto schon in Bewegung gesetzt hat, bevor du den Timer gestartet hast (also bevor t = 0).

Wenn du dir nun den y-Achsenabschnitt (x = 0) ansiehst, ist t = 0 der Punkt, an dem du begonnen hast, die Zeit zu messen. Der Wert von y an diesem Punkt gibt also die Startposition (Entfernung) des Autos in Bezug auf dich an. Dieser Wert ist, wie wir bereits besprochen haben, gleich dem Wert von b in der Normalform einer Geradengleichung.

Wenn du dir jetzt den x-Achsenabschnitt (y = 0) ansiehst, ist das der Punkt, an dem der Abstand zwischen dem Auto und dir 0 ist. Dann ist der Wert von x an diesem Punkt der Zeitpunkt, an dem du und das Auto am selben Ort waren. Hoffen wir, dass du im Auto warst und nicht darunter.

Das obige Autobeispiel ist ein sehr einfaches Beispiel, das dir helfen soll, zu verstehen, wieso die Hauptform einer Geradengleichung wichtig ist und was genau die Schnittpunkte bedeuten. In diesem Artikel sprechen wir hauptsächlich über Geraden. Die Schnittpunkte können aber für jede Art von Kurve berechnet werden (wenn sie eine Achse schneidet).

Tatsächlich passt das obige Beispiel nicht zu einer linearen Gleichung und hat trotzdem Schnittpunkte mit der x-Achse und der y-Achse. Das Gleiche gilt für jede andere Parabel und andere Funktionsgraphen.

Eine Gleichung, die garantiert einen y-Abschnitt, aber nicht unbedingt einen x-Abschnitt hat, ist eine Parabel. Diese Gleichung ist in der Abbildung oben dargestellt. Sie hat ein Maximum oder ein Minimum (je nach Ausrichtung). Wenn dieses Maximum unter der x-Achse oder das Minimum über der x-Achse liegt, wird sie keinen x-Achsenabschnitt haben.

Es sind jedoch nicht alle Gleichungen gleich. Einige der Formeln beschreiben Kurven, die nie einen Schnittpunkt mit der x-Achse, der y-Achse oder mit beiden haben werden. Schauen wir uns etwas genauer an, wie das sein kann.

Wir können 3 Gruppen von Gleichungen unterscheiden, je nachdem, ob sie nur einen y-Achsenabschnitt, nur einen x-Achsenabschnitt oder keines von beiden haben. Die erste Gruppe (nur y-Achsenabschnitt) kann fast jede Art von Gleichung enthalten, auch lineare Gleichungen. Ein gutes und einfaches Beispiel ist y = 3 (oder jeder andere konstante Wert von y größer oder kleiner als 0), da dies eine Linie ist, die parallel zur x-Achse verläuft und diese daher nie schneidet. Bitte versuche nicht, diese Art von Schnittpunkten mit dem Hauptform-einer-Geradengleichung-Rechner zu berechnen, da diese Art von Gleichungen möglicherweise das Internet zerstören kann.

Die zweite und dritte Gruppe von Gleichungen sind etwas schwieriger zu verstehen. Um sie gut zu verstehen, müssen wir das Konzept der Asymptote einführen. Eine Asymptote ist eine Linie (die als lineare Gleichung ausgedrückt werden kann), welcher sich die Funktion oder Kurve, von der wir sprechen, immer mehr annähert, die diese Linie aber nie schneidet oder berührt.

Schauen wir uns eine Beispielgleichung an, um diese Definition besser zu verstehen. Nehmen wir die Gleichung y = 1/x. Wenn wir versuchen, den Schnittpunkt von y zu finden, indem wir x = 0 einsetzen, erhalten wir einen mathematisch unbestimmten Ausdruck, da es nicht möglich ist, durch 0 zu teilen.

Wenn wir Werte nehmen, die immer näher an 0 liegen (etwa 0,1, dann 0,001, 0,000001...), können wir sehen, dass der Wert von y sehr schnell ansteigt. Um den Punkt x = 0 herum ist y also sehr groß. Aufgrund der Regeln der Mathematik gibt es aber keinen definierten Wert für genau diesen Punkt. Manchmal sagt man 1/0 = ∞, aber in Wirklichkeit ist die Unendlichkeit keine Zahl, sondern ein Konzept.

In diesem Fall stellt die lineare Gleichung x = 0 die Asymptote der Funktion y = 1/x dar, was bedeutet, dass y = 1/x niemals diese Linie schneidet und somit auch keinen y-Achsenabschnitt hat. Generell gilt, dass immer dann, wenn eine Funktion eine Asymptote hat, welche auf einer der Achsen liegt, mindestens ein Schnittpunkt nicht gegeben ist.

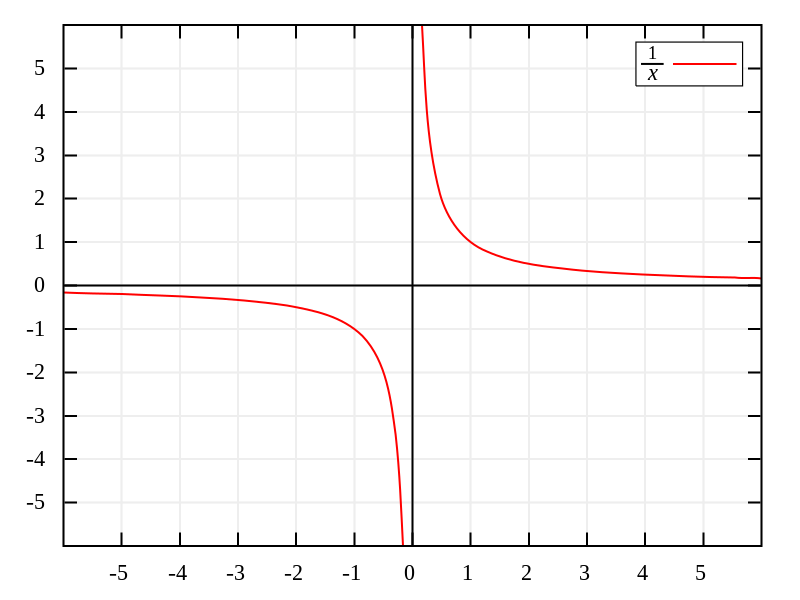
Das Beispiel, das wir dir gezeigt haben (y = 1/x), hat auch eine Asymptote für y = 0, d. h. die x-Achse. Aus demselben Grund wie zuvor ist y = 0 niemals mit der Formel erreichbar, denn dazu müsste x = ∞ sein, und wie wir bereits gesagt haben, ist das unmöglich, denn Unendlichkeit ist ein Konzept und keine Zahl.

Bevor wir uns dem nächsten Thema zuwenden, wollen wir anmerken, dass wir das Thema Unendlichkeit hier extrem vereinfacht haben. Wir glauben aber, dass dies ein guter und schneller Ansatz für diejenigen ist, die mit dem Konzept der Unendlichkeit in der Mathematik weniger vertraut sind. Wir empfehlen dir, mehr über den richtigen Umgang mit dem Unendlichen zu lernen, beginnend mit den unbestimmten Ausdrücken in der Mathematik.

Man könnte leicht denken, dass der Nutzen von linearen Gleichungen aufgrund ihrer Einfachheit sehr begrenzt ist. In der Realität sind lineare Gleichungen jedoch der Kern einiger der mächtigsten Methoden zur Lösung von Minimierungs- und Optimierungsproblemen.

Minimierungsprobleme sind eine Art von Problemen, bei denen man herausfinden möchte, wie eine der Variablen so klein wie möglich gemacht werden kann. Diese Variable könnte z. B. der Unterschied zwischen der Vorhersage eines Wertes von einem Computeralgorithmus und dem tatsächlichen Wert sein. Diese Art von Problemen gehört zu den häufigsten Problemen und steht im Mittelpunkt von maschinellem Lernen und wissenschaftlichen Experimenten.

Eine der gebräuchlichsten und leistungsfähigsten Methoden, um den Minimalwert einer Gleichung oder Formel zu finden, ist das sogenannte Newtonverfahren, benannt nach dem Genie, das es erfunden hat. Das Verfahren verwendet Ableitungen, lineare Gleichungen und x-Achsenabschnitte:

Diese Methode besteht darin, einen Wert für x zu wählen und die Ableitung der Gleichung an diesem Punkt zu berechnen. Mithilfe der Ableitung, als Steigung einer linearen Gleichung, die genau durch den Punkt (x, y) verläuft, wird der x-Achsenabschnitt berechnet. Dies ist eine der Situationen, in denen die Hauptform einer Geradengleichung nützlich ist.

Sobald der x-Achsenabschnitt berechnet ist, wird dieser Wert von x benutzt, um den obigen Prozess eine bestimmte Anzahl von Malen zu wiederholen, bis wir zu einem Wert von y kommen, der minimal ist (was bedeutet, dass die Ableitung 0 sein wird). Für Probleme des realen Lebens würde es unendlich lange dauern, den exakten Minimalwert zu finden, normalerweise ist daher ein Näherungswert ausreichend für die Lösung des Problems.

Ein sehr häufiges Beispiel ist die Anwendung der Methode der kleinsten Quadrate, um Daten an eine Formel anzupassen. In diesem Fall ist der Wert, den wir minimieren wollen, die Summe des quadratischen Abstands zwischen den Funktionswerten und den Datenpunkten, wobei der Abstand entlang einer senkrechten Linie vom Punkt zur Funktionsgeraden berechnet wird.

In der Achsenabschnittsform wird eine Gerade durch ihre Schnittpunkte mit den Koordinatenachsen dargestellt. Wenn wir diese Schnittpunkte als (x0, 0) und (0, y0) darstellen, so sieht die Achsenabschnittsform dieser Geraden folgendermaßen aus: x/x0 + y/y0 = 1. Alle Wertpaare, die diese Gleichung erfüllen, entsprechen den Koordinaten eines Punktes, welcher auf dieser Geraden liegt.

Wenn du zwei auf der Geraden liegende Punkte kennst, kannst du die Geradengleichung so aufstellen:

1. Berechne die Differenz zwischen den x-Koordinaten des ersten und des zweiten Punktes: Δx = x1-x2.
2. Berechne die Differenz zwischen den y-Koordinaten des ersten und des zweiten Punktes: Δy = y1-y2.
3. Bestimme die Steigung, indem du die Differenz der y-Koordinaten durch die Differenz der x-Koordinaten teilst: m = Δy/Δx.
4. Setze nun diesen Wert und die Koordinaten eines der Punkte in die Geradengleichung ein, um den Wert von b zu bestimmen, z. B.: y1 = mx1 + b, also

b = y1 - mx1

Die Steigung (auch Gradient genannt) beschreibt die Steilheit einer Linie. Die Steigung kann positiv, negativ oder gleich null sein:

• Eine positive Steigung bedeutet, dass die Linie von links nach rechts ansteigt.
• Negative Steigung bedeutet, dass die Linie von links nach rechts abwärts verläuft.
• Steigung gleich null bedeutet, dass die Linie waagerecht ist.

Je größer der absolute Wert der Steigung ist, desto schneller steigt/sinkt die Linie. Tatsächlich ist der Wert der Steigung genau der Betrag, um den die Linie ansteigt/abfällt, wenn sich x um eine Einheit erhöht.

Die Steigung ist m = 1. Um dieses Ergebnis zu erhalten, verwende die Formel m = tan(α), wobei α der Winkel zwischen der Linie und der x-Achse ist. Da tan(45°) = 1 ist, ergibt sich die Steigung 1.