Last updated: Apr 30, 2024

Spezielle rechtwinklige Dreiecke Rechner

Q: Wie lauten die Formeln für ein 45-45-90 Dreieck?

Für ein 45°-45°-90° Dreieck gelten folgende Formeln, wobei x die Länge einer der gleichen Seiten ist: Hypotenuse = x√2 ; Flächeninhalt = x²/2 ; und Umfang = x(2+√2) . Read more

Q: Ist 3, 4 und 5 ein Pythagoreisches Tripel?

Ja . Die ganzen Zahlen a = 3 , b = 4 und c = 5 bilden ein pythagoreisches Tripel, da a² + b² = c² und ein Dreieck mit den Seiten abc ein rechtwinkliges Spezialdreieck ist. Read more

Table of contents

Spezielle rechtwinklige Dreiecke 30-60-90 Spezielles rechtwinklige Dreiecke 45-45-90 Andere spezielle rechtwinklige Dreiecke Formeln für spezielle rechtwinklige Dreiecke Regeln für spezielle rechtwinklige Dreiecke Rechner für spezielle rechtwinklige Dreiecke – Beispiel FAQs

Dieser Rechner für spezielle rechtwinklige Dreiecke hilft dir im Handumdrehen, dein Dreieck zu lösen. Wähle das Dreieck aus, das du brauchst, und gib die bekannten Werte ein – die restlichen Parameter werden automatisch berechnet.

Die speziellen rechtwinkligen Dreiecke sind rechtwinklige Dreiecke, für die es einfache Formeln gibt. Das ermöglicht schnelle Berechnungen, sodass du nicht den Satz des Pythagoras oder eine fortgeschrittene Methode anwenden musst. Scrolle nach unten, um mehr über die Formeln und Regeln für spezielle rechtwinklige Dreiecke zu erfahren.

Spezielle rechtwinklige Dreiecke 30-60-90

Das spezielle rechtwinklige Dreieck $30\degree$ $60\degree$ $90\degree$ ist eines der beliebtesten rechtwinkligen Dreiecke. Seine Eigenschaften sind einzigartig, da es die Hälfte eines gleichseitigen Dreiecks ist.

Spezielles rechtwinkliges Dreieck: 30-60-90.

Wenn du mehr über diese spezielle Form erfahren möchtest, schau dir unseren 30° 60° 90° Dreiecksrechner an.

Spezielles rechtwinklige Dreiecke 45-45-90

Ein weiteres berühmtes spezielles rechtwinkliges Dreieck ist das $45\degree$ $45\degree$ $90\degree$ Dreieck. Es ist das einzig mögliche rechtwinklige Dreieck, das auch ein gleichschenkliges Dreieck ist. Außerdem ist es die Form, die entsteht, wenn wir ein Quadrat entlang seiner Diagonale schneiden:

Spezielles rechtwinkliges Dreieck: 45-45-90 mit einer bestimmten Schenkellänge.

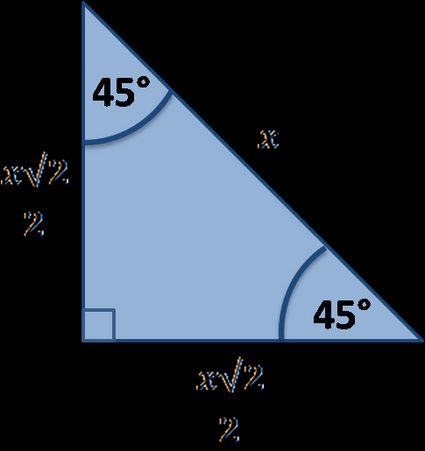
Spezielles rechtwinkliges Dreieck: 45-45-90 mit einer bestimmten Länge der Hypotenuse.

Bist du neugierig auf die Eigenschaften dieses Dreiecks? Schau dir unseren 45° 45° 90° Dreieck Rechner an.

Andere spezielle rechtwinklige Dreiecke

Es gibt viele spezielle rechtwinklige Dreiecke, unten findest du die, die in unserem Tool implementiert sind:

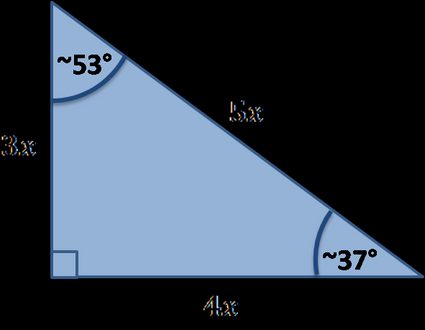
Spezielles rechtwinkliges Dreieck: 3x-4x-5x.

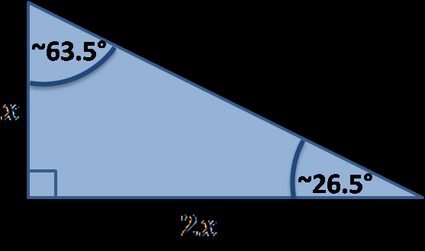
Spezielles rechtwinkliges Dreieck: b=2a.

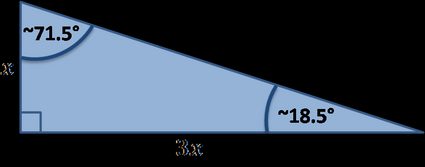
Spezielles rechtwinkliges Dreieck: b=3a.

Formeln für spezielle rechtwinklige Dreiecke

Rechtwinkliges Dreieck mit den Seiten a, b, c und den Winkeln α, β.

Wenn du nach den Formeln für spezielle rechtwinklige Dreiecke suchst, bist du hier richtig. Sieh dir diese übersichtliche Tabelle unten an, dann sollte alles klar sein! In dieser Tabelle findest du die Formeln für die Beziehung zwischen den Winkeln, Schenkeln, der Hypotenuse, dem Flächeninhalt und dem Umfang eines rechtwinkligen Dreiecks:

Spezielles rechtwinkliges Dreieck	$a$ (Kürzerer Schenkel)	$b$ (Längerer Schenkel)	$c$ (Hypotenuse)	Fläche	Umfang	Winkel $\alpha$	Winkel $\beta$
$30\degree$ - $60\degree$ - $90\degree$	$x$	$x\sqrt 3$	$2x$	$x^2\sqrt{3}/2$	$x(3+\sqrt3)$	$30\degree$	$60\degree$
$45\degree$ - $45\degree$ - $90\degree$	$x$	$x$	$x\sqrt 2$	$x^2/2$	$x(2+\sqrt 2)$	$45\degree$	$45\degree$
$x$ - $2x$	$x$	$2x$	$x\sqrt5$	$x^2$	$x(3+\sqrt 5)$	$\approx26,\!5\degree$	$\approx63,\!5\degree$
$x$ - $3x$	$x$	$3x$	$x\sqrt {10}$	$3x^2/2$	$x(4+\sqrt{10})$	$\approx18,\!5\degree$	$\approx71,\!5\degree$
$3x$ - $4x$ - $5x$	$3x$	$4x$	$5x$	$6x^2$	$12x$	$\approx37\degree$	$\approx53\degree$

Regeln für spezielle rechtwinklige Dreiecke

Spezielle rechtwinklige Dreiecke sind Dreiecke, die einige besondere Eigenschaften haben, die ihre Berechnungen erleichtern. Die wichtigste Regel für rechtwinklige Dreiecke ist natürlich, dass sie einen rechten Winkel und diese zusätzliche Eigenschaft haben müssen. Im Allgemeinen lassen sich rechtwinklige Dreiecke in zwei Gruppen einteilen:

Winkelbasierte rechtwinklige Dreiecke – zum Beispiel $30\degree$ - $60\degree$ - $90\degree$ und $45\degree$ - $45\degree$ - $90\degree$ Dreiecke.
Seitenbasierte rechtwinklige Dreiecke – Figuren, deren Seitenlängen von einer bestimmten Regel bestimmt werden, z. B.:
- Seiten mit ganzzahligen Längen werden pythagoreische Tripel genannt:
  
  $3:4:5$ , $5:12:13$ , $8:15:17$ , $7:24:25$ , $9:40:41$ ..
- Seiten mit ganzzahligen Längen, aber fast gleichschenklig:
  
  $20:21:29$ , $119:120:169$ , $696:697:985$ ..
- Rechtwinkliges Dreieck, dessen Seiten eine geometrische Folge sind (Kepler-Dreieck). Es wird von drei quadratischen Seiten gebildet. Ihre Flächeninhalte stehen in geometrischer Folge, entsprechend dem Goldenen Schnitt. Mehr darüber erfährst du in unserem Goldener Schnitt Rechner.

Es gibt viele verschiedene Regeln und Möglichkeiten, nach denen wir das Dreieck auswählen und es speziell nennen können. In unserem Rechner für spezielle rechtwinklige Dreiecke haben wir fünf Dreiecke ausgewählt: zwei winkelbasierte und drei seitenbasierte.

Rechner für spezielle rechtwinklige Dreiecke – Beispiel

Schauen wir uns das Beispiel an: Wir möchten die Länge der Hypotenuse eines rechtwinkligen Dreiecks finden, wenn die Länge eines Schenkels $5$ cm und ein Winkel $45\degree$ beträgt.

Wähle den richtigen Typ des speziellen rechtwinkligen Dreiecks. In unserem Fall ist es ein $45\degree$ - $45\degree$ - $90\degree$ Dreieck.
Gib den bekannten Wert ein. Wir wissen, dass die Seite $5$ ist, also geben wir diesen Wert in das Feld a oder b ein – es ist egal, wo, denn es handelt sich um ein gleichschenkliges Dreieck.
Wow! Der Rechner für spezielle rechtwinklige Dreiecke hat die Maße deines Dreiecks gelöst! Jetzt wissen wir das:
- Der zweite Schenkel $b$ $5\ \mathrm{cm}$ ist;
- Die Hypotenuse $c$ ist $7,\!07\ \mathrm{cm}$ ;
- Der Umfang ist $17,\!07\ \mathrm{cm}$ ; und
- Der Flächeninhalt unseres speziellen Dreiecks beträgt $12,\!5\ \mathrm{cm^2}$ .

Warte nicht länger. Versuche es selbst!

FAQs

Wie lauten die Formeln für ein 45-45-90 Dreieck?

Für ein 45°-45°-90° Dreieck gelten folgende Formeln, wobei x die Länge einer der gleichen Seiten ist:

Hypotenuse = x√2;
Flächeninhalt = x²/2; und
Umfang = x(2+√2).

Wie löse ich das spezielles rechtwinkliges Dreieck 30-60-90?

Um ein rechtwinkliges Dreieck mit 30°, 60° und 90° zu lösen, gehst du folgendermaßen vor:

Finde die Länge des kürzeren Schenkels. Wir nennen sie x.
Der längere Schenkel beträgt x√3.
Seine Hypotenuse ist 2x.
Der Flächeninhalt ist A = x²√3/2.
Der Umfang ist P = x(3 + √3).

Was sind die beiden besonderen Dreiecke in der Trigonometrie?

30°-60°-90° Dreiecke und 45°-45°-90° (oder gleichschenkliges rechtwinkliges Dreieck) sind die beiden besonderen Dreiecke in der Trigonometrie. Es gibt zwar mehr als zwei verschiedene rechtwinklige Dreiecke, aber diese sind am schnellsten zu erkennen und am einfachsten zu berechnen. Ein Beispiel für ein spezielles rechtwinkliges Dreieck, das nicht auf einem Winkel basiert, ist ein rechtwinkliges Dreieck, dessen Seiten ein Pythagoreisches Tripel bilden.

Ist 3, 4 und 5 ein Pythagoreisches Tripel?

Ja. Die ganzen Zahlen a = 3, b = 4 und c = 5 bilden ein pythagoreisches Tripel, da a² + b² = c² und ein Dreieck mit den Seiten abc ein rechtwinkliges Spezialdreieck ist.

Spezielles Dreieck

a

b

c

Umfang

Flächeninhalt

Check out 19 similar triangle calculators 🔺

30 60 90 triangle45 45 90 triangleArea of a right triangle...16 more