Richtung eines Vektors Rechner

Wenn du die Richtung eines Vektors berechnen möchtest, bist du hier richtig. Dieser Rechner findet den Richtungswinkel eines Vektors und berechnet einen Einheitsvektor in dieser Richtung.

Vektoren sind ein mächtiges Werkzeug, um viele Mengen in unserer physikalischen Welt darzustellen. Sie stellen Kräfte, Geschwindigkeiten und viele andere Mengen dar, die von ihnen abgeleitet werden.

Neben der Richtung kannst du auch den Vektorbetrag bestimmen, wenn du die Option Erweiterter Modus des Rechners wählst. Mit diesem Tool kannst du also den Vektorbetrag und den Richtungswinkel eines beliebigen Vektors ermitteln.

Du kannst die Richtung eines Vektors v auf zwei Arten ausdrücken oder berechnen:

1. Berechne den Richtungswinkel des Vektors v. Der Richtungswinkel ist der Winkel, den v mit der positiven x-Achse bildet, wobei gegen den Uhrzeigersinn gezählt wird.
2. Berechne einen Einheitsvektor in der Richtung desselben Vektors. Dieser Einheitsvektor wird Richtungsvektor genannt.

Um den Winkel $\theta$ zu berechnen, den ein zweidimensionaler Vektor $\vec{v} = (x, y)$ mit der horizontalen Achse bildet, benutze diese Gleichung:

Das einzige Problem bei dieser Gleichung ist, dass sie uns nicht den Winkel um die positive x-Achse liefert, sondern nur um die nächstgelegene horizontale Achse. Wenn dein Vektor im ersten Quadranten der kartesischen Ebene liegt, wie der Vektor, der im Bild auf $P(3, 5)$ zeigt, ist das kein Problem.

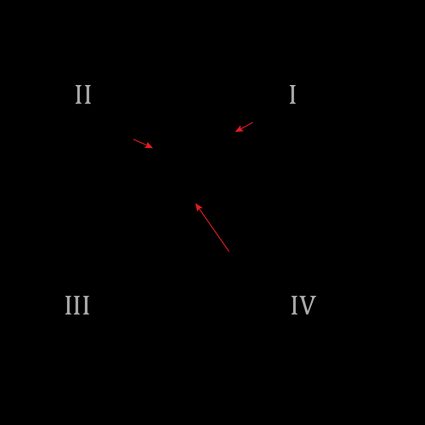
Aber was ist, wenn der Vektor in einem der anderen Quadranten liegt? Angenommen, du möchtest den Richtungswinkel $\theta$ des Vektors $Q = (-2, 4)$ aus dem vorherigen Bild finden. Wenn wir die obige Formel verwenden würden, um den Richtungswinkel zu bestimmen, würden wir nicht den richtigen Winkel erhalten, da wir den Winkel $\gamma$ anstatt des Richtungswinkels $\theta$ erhalten würden.

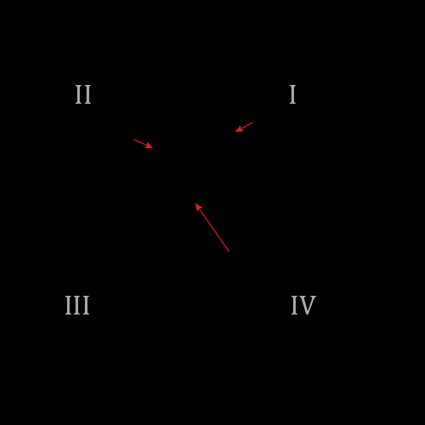
Was können wir dann tun? Nun, in diesem Fall könntest du festgestellt haben, dass $\theta = 180^\circ - \gamma$. Wir können diese Überlegung auf die anderen Fälle ausweiten und die folgenden Gleichungen aufstellen, um die Richtung des Vektors in jedem Quadranten zu berechnen:

• Im ersten Quadranten, $\theta_\text{I} = \arctan(\frac{y}{x})$.
• Im zweiten Quadranten, $\theta_\text{II} = 180° - \arctan(\frac{y}{x})$.
• Im dritten Quadranten, $\theta_\text{III} = 180° + \arctan(\frac{y}{x})$.
• Im vierten Quadranten, $\theta_\text{IV} = 360° - \arctan(\frac{y}{x})$.

Um einen Einheitsvektor û in Richtung eines anderen Vektors v = (x, y, z) zu finden, gehe folgendermaßen vor:

1. Finde den Vektorbetrag des Vektors v:

   |v| = √(x² + y² + z²)

2. Dividiere jeden Koeffizienten des Vektors v durch den Vektorbetrag von v:

   û = v/|v| = (x/|v|, y/|v|, z/|v|)

3. Das war's. û ist der Einheitsvektor in Richtung von v.

Um den Vektor eines bestimmten Vektorbetrags in Richtung eines anderen Vektors zu finden v = (x, y, z):

1. Finde den Vektorbetrag des Vektors v:

   |v| = √(x² + y² + z²)

2. Finde einen Einheitsvektor û in der Richtung von v. Dazu dividierst du jeden Koeffizienten des Vektors v durch den Vektorbetrag:

   û = v/|v| = (x/|v|, y/|v|, z/|v|)

3. Multipliziere den Vektorbetrag des gewünschten Vektors mit dem Einheitsvektor û. Das Ergebnis ist der gewünschte Vektor.

Um den Vektorbetrag und die Richtung von zwei Vektoren zu bestimmen, musst du den resultierenden Vektor finden (du kannst dazu unseren Vektoraddition Rechner verwenden) und die oben beschriebenen Schritte auf ihn anwenden.

Da du nun weißt, wie du den Vektorbetrag und den Richtungswinkel eines Vektors bestimmen kannst, schauen wir uns einige Zahlenbeispiele und FAQs an.

Suche einen Vektor des Vektorbetrags 3 in Richtung v = 12i - 5k:

1. Finde den Vektorbetrag von v:

   |v| = √(12² + (-5)²) = 13

2. Finde einen Einheitsvektor û in Richtung von v. Dividiere dazu v durch seinen Vektorbetrag:

   û = v/|v| = (12/13)i - (5/13)k

3. Multipliziere den gewünschten Vektorbetrag 3 mit dem Einheitsvektor û. Wir erhalten den Vektor w:

   w = 3û = (36/13)i - (15/13)k,

   der die gewünschte Richtung und den gewünschten Vektorbetrag hat.

Um einen Einheitsvektor in Richtung v = i + j + 2k zu berechnen:

1. Finde den Vektorbetrag von v:

   |v| = √(1² + 1² + 2²) = √6 ≈ 2,4495

2. Dividiere den Vektor v durch seinen Vektorbetrag:

   û = v/|v| = (1/√6)i + (1/√6)j + (2/√6)k

3. Das war's. û ist der Einheitsvektor in der Richtung von v.

Das Skalarprodukt zweier Vektoren, die in dieselbe Richtung weisen, ist immer positiv. Das liegt daran, dass das Skalarprodukt zweier gleichgerichteter Vektoren gleich der Multiplikation ihrer Vektorbeträge ist, und ihre Vektorbeträge sind immer positiv.

Bestimme den Vektorbetrag und die Richtung der Summe zweier Vektoren:

1. Finde die Resultierende der beiden Vektoren.
2. Quadriere die einzelnen Komponenten des resultierenden Vektors.
3. Ziehe die Quadratwurzel aus dem vorherigen Ergebnis. Das ist der Vektorbetrag der Summe deiner beiden Vektoren!
4. Um die Richtung des Vektors v = (x, y) zu berechnen, verwende die Formel θ = arctan(y/x), wobei θ der kleinste Winkel ist, den der Vektor mit der horizontalen Achse bildet, und x und y die Komponenten des resultierenden Vektors sind.