Logarithmus Rechner

Mit diesem Logarithmus Rechner (Log Rechner) kannst du den Logarithmus einer (positiven, reellen) Zahl zu einer beliebigen Basis (positiv, nicht gleich 1) berechnen. Egal, ob du den natürlichen Logarithmus berechnen möchtest, den Logarithmus zur Basis 2 oder zur Basis 10 suchst, der Rechner kann als Log2 Rechner, dekadischer Logarithmus Rechner, usw. verwendet werden.

Lies im Text des Logarithmusrechners weiter, um ein tieferes Verständnis über das Prinzip und die Rechengesetze von Logarithmen zu bekommen. Der Text hält zudem einige spannende und eventuell überraschende Beispiele für die Anwendung und das Vorkommen von Logarithmen in unserem Alltag bereit.

Falls du zudem auf der Suche nach anderen nützlichen Mathematikrechnern bist, wirf einen Blick auf unseren Kubikwurzel Rechner, mit dem du die Kubikwurzel (dritte Wurzel) aber auch jede andere beliebige Wurzel ziehen kannst.

Manchmal sind Zusammenhänge einfacher durch Visualisierungen zu verstehen. Schaue dir unser Youtube Video über Logarithmen an, um in 90 Sekunden den vollen Überblick haben:

Eine Logarithmus-Funktion ist eine Umkehrung der Exponentialfunktion. Wenn a hochgezählt y x ergibt, dann ist der Logarithmus von x zur Basis a gleich y. In Form von Gleichungen ist aʸ = x gleichbedeutend mit logₐ(x) = y.

Mit anderen Worten: Der Logarithmus von x oder logₐ(x) zeigt, auf welche Potenz wir a erhöhen müssen (oder, wenn x größer als 1 ist, wie oft a mit sich selbst multipliziert werden muss), um den Wert x zu erhalten. Aus dieser Sicht können wir den Logarithmus auch auf folgende Weise darstellen:

$\mathrm{a^{{log}_a(x)}} =\mathrm x$

Hoffentlich hast du jetzt die Definition des Logarithmus verstanden; im folgenden Abschnitt kannst du seine beiden am häufigsten verwendeten Formen nachlesen.

Du kannst verschiedene Zahlen als Basis für den Logarithmus wählen; zwei besondere Basen werden jedoch so häufig verwendet, dass Mathematiker ihnen eindeutige Namen gegeben haben: der natürliche Logarithmus und der gemeinsame Logarithmus.

Natürlicher Logarithmus

Wenn du den natürlichen Logarithmus einer Zahl berechnen möchtest, musst du eine Basis wählen, die ungefähr gleich 2,718281 ist. Üblicherweise wird diese Zahl mit e bezeichnet, benannt nach Leonard Euler, der ihren Wert im Jahr 1731 definierte. Dementsprechend kann der Logarithmus als logₑx dargestellt werden, aber traditionell wird er mit dem Symbol ln(x) bezeichnet. In der Finanz- und Wirtschaftswissenschaft wird für die gleiche Funktion auch die Bezeichnung log(x) verwendet. Also y = logₑx = ln(x), was gleichbedeutend ist mit x = eʸ = exp(y).

Eine praktische Möglichkeit, den natürlichen Logarithmus zu verstehen, ist, ihn im Zusammenhang mit [Zinseszins](calc: 12) zu betrachten. Das sind die Zinsen, die sowohl auf das Kapital als auch auf die aufgelaufenen Zinsen berechnet werden.

Die Formel für den jährlichen Zinseszins lautet wie folgt:

A = P(1 + r/m)ᵐᵗ

wobei:

• A — Wert der Investition nach t Jahren;
• P — Ausgangswert;
• r — Jährlicher Zinssatz (in Dezimalen);
• m — Anzahl der Zinsaufschläge pro Jahr oder Aufzinsungshäufigkeit; und
• t — Anzahl der Jahre.

Nehmen wir an, du legst Geld für ein Jahr bei einer Bank mit einem sehr hohen Jahreszins von 100% (entsprechend r = 1) an, bei der die Zinseszinsen häufig anfallen (m ist also groß). Es ist leicht zu erkennen, wie schnell der Wert von m steigt, wenn du die jährliche (m = 1), monatliche (m = 12), tägliche (m = 365) oder stündliche (m = 8.760) Häufigkeit vergleichst. Stell dir nun vor, dass dein Geld jede Minute oder Sekunde neu berechnet wird, so dass m riesig ist.

Schauen wir uns nun an, wie sich die wachsende Frequenz auf dein Ausgangsgeld auswirkt:

Du wirst feststellen, dass der Wert (1 + 1/m)ᵐ (der Multiplikator deiner Ersteinzahlung) nicht sehr stark ansteigt, obwohl die Häufigkeit der Aufzinsung eine ungewöhnlich hohe Zahl erreicht. Stattdessen wird er einigermaßen stabil: Er nähert sich dem oben bereits erwähnten Wert e ≈ 2,718281.

Da die Wachstumsraten oft einem ähnlichen Muster folgen wie im obigen Beispiel, wird in den Wirtschaftswissenschaften viel mit natürlichen Logarithmen gearbeitet. Zwei gängige Variablen haben mit dem natürlichen Logarithmus zu tun: die [BIP-Wachstumsrate](calc: 1252) und die [Preiselastizität der Nachfrage](calc: 599).

Zehnerlogarithmus/ dekadische Logarithmus

Die andere gängige Form des Logarithmus ist der Zehnerlogarithmus mit der Basis 10, log₁₀x, der üblicherweise als lg(x) bezeichnet wird. (Manchmal wird der dekadische Logarithmus aber auch als log(x) geschrieben. Wenn du diese Bezeichnung siehst, achte also darauf, dass du die Absicht des Autors genau überprüfst!) Er ist auch als dezimaler Logarithmus, dekadischer Logarithmus, Standard Logarithmus oder Briggs'scher Logarithmus bekannt, benannt nach Henry Briggs, einem englischen Mathematiker, der seine Verwendung entwickelt hat.

Wie der Name schon sagt, ist er die am häufigsten verwendete Form des Logarithmus. Er wird zum Beispiel in unserem Dezibel-Rechner verwendet. Logarithmentabellen, die in der Vergangenheit das Rechnen erleichtern sollten, stellten meist auch natürliche Logarithmen dar.

In der folgenden Tabelle sind einige häufige Werte des natürlichen und des gewöhnlichen Logarithmus aufgeführt. Mit 0+ bezeichnen wir den Wert, dem sich der Logarithmus nähert, wenn sich x von oben her 0 nähert.

Stell dir vor, du möchtest den Logarithmus berechnen für eine Zahl mit einer beliebigen Basis, hast aber nur einen Rechner für den natürlichen und dekadischen Logarithmus zur Verfügung. Wende in diesem Fall folgende Formeln an:

• logₐ(x) = ln(x) / ln(a)
• logₐ(x) = lg(x) / lg(a)

Nehmen wir an, du möchtest mit diesem Logarithmus Rechner einen Logarithmus zur Basis 2 für eine beliebige Zahl berechnen:

1. Bestimme die Zahl, deren Logarithmus du ermitteln möchtest. Nehmen wir an, es ist 100.
2. Bestimme die Basis – in unserem Fall 2.
3. Finde den Logarithmus von 100 zur Basis 10. lg(100) = 2.
4. Finde mit dem Rechner den Logarithmus von 2 zur Basis 10. lg(2) = 0,30103.
5. Teile diese zwei Werte: lg(100)/lg(2) = 2 / 0,30103 = 6,644.
6. Du kannst die Schritte 3-5 natürlich auch unserem Logarithmusrechner überlassen.

Es gibt Hinweise darauf, dass der Begriff des Logarithmus bereits im 8. Jahrhundert in Indien bekannt war. Das entwickelte Konzept des Logarithmus erschien jedoch zum ersten Mal in dem Buch mit dem Titel Mirifici logarithmorum canonis descriptio (die Konstruktion des wunderbaren Kanons der Logarithmen), das 1614 gedruckt wurde. Es war das Ergebnis 20-jähriger Forschungen des schottischen Mathematikers John Napier, der sich zum Ziel gesetzt hatte, Berechnungen zu vereinfachen, auf die er als Astronom und Physiker gestoßen war.

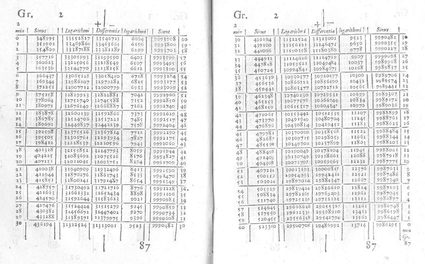
Der erste Teil des Buches erklärt die Eigenschaften und Anwendungen von Logarithmen. Der zweite Teil veranschaulicht Beispiele für logarithmische Berechnungen auf neunzig Seiten mit Tabellen. Napier weist auch auf die Grenzen seines Werks hin und liefert Analogien, Beispiele, Warnungen, Mahnungen und Schlussfolgerungen. Daher kann das Buch auch als Gebrauchsanweisung dienen. Er geht jedoch nicht näher darauf ein, wie das Werkzeug entwickelt wurde.

Da die meisten komplexeren Rechenoperationen unseres heutigen Alltags oft durch Computeralgorithmen für uns ausgeführt und uns somit abgenommen werden, ist es vielleicht etwas schwer, die Erfindung des Logarithmus so sehr wertzuschätzen. Doch im 17. Jahrhundert war dies eine bahnbrechende Entdeckung, welche das Leben der Menschen revolutionierte. Die Lösung mathematischer Probleme ohne den Log berechnen zu können konnte Stunden, Tage oder sogar Jahre dauern.

Einer der ersten bedeutenden Fortschritte, den Logarithmen mit sich brachten, war die Vereinfachung von langen und komplexen Multiplikations- und Divisionsaufgaben durch Umwandlung dieser in leichtere Additions- und Subtraktionsaufgaben (heute als Rechenregeln für Logarithmen bekannt). Der einzige zusätzliche Aufwand war das Nachschlagen von Logarithmen und Antilogarithmen in Tabellen.

Das neue Rechenverfahren war auf dem Gebiet der Astronomie von entscheidender Bedeutung. Napiers wissenschaftliche Aktivitäten fielen mit der Ära der neuen Entwicklungen in der Astrophysik zusammen. So kämpften viele Astronomen mit endlosen Berechnungen, um die Position der Planeten anhand von Kopernikus' Theorie des Sonnensystems zu bestimmen. Johannes Kepler, der zu dieser Zeit an seinen berühmten Gesetzen über die Bewegungen der Planeten arbeitete, war unter ihnen.

Dank Napiers Bemühungen konnte er sein Arbeitspensum, das bis dahin fast tausend Seiten an Berechnungen erforderte, erheblich reduzieren und sich so mehr Zeit für philosophische Spekulationen nehmen.

Der berühmte britische Mathematiker Henry Briggs erkannte schnell die Möglichkeiten der neuen Erfindung: Er zog nach Schottland, um Napier zu treffen, damit sie gemeinsam nach möglichen Fortschritten suchen konnten.

Nachdem sie die ursprüngliche Idee modifiziert hatten, formulierten sie 1617 die erste Tabelle der Logarithmen, die auf Potenzen von 10 basiert. 1624, nach Napiers Tod, veröffentlichte Briggs sein Buch Arithmetica logarithmic, in dem er Logarithmentafeln für 30 Tausend natürliche Zahlen mit 14 Dezimalstellen vorstellte. Diese Form der Logarithmen wird heute als Gemeinsamer Logarithmus bezeichnet.

Die wachsende Popularität dieses neuen mathematischen Instruments regte zu weiteren Forschungen an. Im Jahr 1620 stellte Edmund Gunter den Rechenschieber für den Logarithmus vor, ein physikalischer Log Rechner, das für Multiplikationen und Divisionen verwendet wurde.

Die frühe Version des Instruments, die zum Messen einen Zirkel erforderte, wurde um 1622 von William Oughtred weiterentwickelt. Er entwarf den herkömmlichen Rechenschieber, ein Gerät mit zwei nebeneinander gleitenden Linealen.

Oughtreds Erfindung erleichterte die Berechnung von Logarithmen weiter. Rechenschieber wurden zu einem Standardrechengerät in Berufen, die Arithmetik erfordern. Architekten, Ingenieure, Wissenschaftler und sogar Astronauten verließen sich bis zum Beginn der digitalen Revolution bei ihren Berechnungen auf sie. Albert Einstein benutzte einen Rechenschieber, und auch die Besatzungen der Apollo-Missionen nahmen Rechenschieber mit ins All.

Im Vergleich zu den frühen Versionen von Computern hatte der Rechenschieber viele Vorteile:

• Er ist klein genug, um in der Tasche zu bleiben;
• Benötigt keine Stromquelle;
• Relativ günstig;
• Mechanisch zuverlässig;
• Einfach in der Funktion; und
• Kann jedes numerische Problem lösen, das mit normalen Bedingungen zu tun hat.

In der heutigen Zeit haben moderne Computer und wissenschaftliche Taschenrechner die oben erwähnten, altmodischen Verfahren ersetzt um den Log zu berechnen. Dennoch hilft dir das Verständnis der Logarithmen, dein allgemeines logisches und mathematisches Verständnis zu erhöhen. Logarithmen finden zahlreiche praktische Anwendungen in alltäglichen sowie wissenschaftlichen Bereichen.

Die Tatsache, dass Logarithmen arithmetische Folgen mit geometrischen Folgen in Beziehung setzen, legt nahe, dass bestimmte Phänomene in der realen Welt ein logarithmisches Muster bilden könnten. In der Tat lassen sich in der Natur zahlreiche Beispiele finden, welche auf Logarithmen zurückzuführen sind und mit dem lg Rechner berechnet werden können.

Die folgenden Naturphänomene zeigen Beispiele logarithmischer Spiralen:

• Schale eines Nautilusschneckenhauses

• Galaxien

• Zyklone

Daneben gibt es weitere Phänomene, die mithilfe logarithmischer Darstellung beschrieben werden:

• Mineralhärte – Mohssche Härteskala,
• Angabe des Schalldruckpegels – Dezibel (dB),
• Windstärke – Beaufortskala,
• Angabe der Stärke von Erdbeben – Richterskala und
• Säure-/ Alkaliegehalt in Lösungen – pH-Wert.

💡Wusstest du, dass die Berechnung der Rauschzahl, welche für die Analysen von Lärmminderungen und -kontrollen von Bedeutung ist, durch Logarithmen erfolgt? Du kannst Genaueres dazu in unserem Rauschzahl Rechner 🇺🇸 herausfinden.

Vor Ende der 1970er Jahre, als Taschenrechner für die breite Öffentlichkeit zugänglich wurden, erforderte die Durchführung von Berechnungen, insbesondere mit Brüchen, einen erheblichen manuellen Aufwand. Um diese mühsame Arbeit zu erleichtern, diente die Anwendung von Logarithmen einer praktischen Funktion.

Um den technischen Vorteil des Logarithmus nutzen zu können, müssen wir mit seinen grundlegenden Eigenschaften vertraut sein. Vermutlich hast du diese Regeln schon kennengelernt, aber die folgende Tabelle zeigt sie dir zur Erinnerung.

Um zu zeigen, wie nützlich das in der Zeit vor dem Taschenrechner war, nehmen wir an, dass du das Produkt von 5,89 × 4,73 ohne ein elektronisches Gerät berechnen musst. Du könntest es auch einfach auf dem Papier ausmultiplizieren, aber das würde ein bisschen Zeit kosten. Stattdessen kannst du die Logarithmus-Regel mit Logarithmentabellen anwenden und erhältst so eine relativ gute Annäherung an das Ergebnis.

Wenn du eine Logarithmentabelle hättest, könntest du den Logarithmus dieser Zahlen schnell überprüfen (oder du suchst im Internet nach einer elektronisch hochgeladenen Tabelle), aber lass uns jetzt ein bisschen schummeln und unseren Taschenrechner für diesen Zweck benutzen.

$\text{lg}(5,\!89) ≅ 0,\!7701153$ und $\text{lg}(4,\!73) ≅ 0,\!674861$

Wenn wir die erste Regel anwenden, können wir die folgende Gleichung umformulieren:

$\text{lg}(5,\!89 \times 4,\!73) =\text{lg}(5,\!89) + \text{lg}(4,\!73) ≅ 0,\!770115 + 0,\!6748611$

$\text{lg}(5,\!89 \times 4,\!73) ≅ 1,\!4449761$

Wir wissen immer noch nicht, wie das genaue Ergebnis lautet, also nehmen wir den Exponenten beider Seiten der obigen Gleichung mit einer kleinen Änderung auf der rechten Seite.

$5,\!89 \times 4,\!73 ≅ 10^{1,\!4449761} = 10^{,\!4449761} \times 10^1$

Jetzt musst du 10^0,4449761 in einer Antilog-Tabelle oder in unserem Antilog-Rechner überprüfen. Wie lautet der Antilog von 0,4449761 zur Basis 10? 2,785968.

Schreibe die Gleichung um:

$5,\!89 \times 4,\!73 ≅ 2,\!785968 \times 10^1 = 27,\!85968$

Wahrscheinlich erscheint das obige Verfahren anspruchsvoller, als die Zahlen einfach in einen Taschenrechner einzugeben oder eine leistungsfähige Anwendung wie unseren Taschenrechner zu benutzen. Um zu zeigen, wie die Macht des Logarithmus dir auch in unserer modernen Zeit helfen kann, betrachten wir die Fakultät 🇺🇸 von 100, die das Produkt aller ganzen Zahlen von 1 bis 100 ist.

$100! = 1 \times 2 \times 3 \times 4 \times ⋯ \times 99 \times 100$

Wenn du versuchen würdest, diese Aufgabe mit einem normalen Taschenrechner zu lösen, würdest du wahrscheinlich scheitern, denn das Ergebnis ist eine riesige Zahl mit vielen Ziffern.

Aber mit Hilfe von Logarithmen kannst du die Operation (mit etwas Rundung) umschreiben als:

$\text{lg100!} = \text{lg1} + \text{lg2} + \text{lg3} + ⋯ + \text{lg100} = 0 + 0,\!30103 + 0,\!47712 + ⋯ + 2 ≅ 157,\!97$

$100! ≅ 10^{0,\!97} \times 10^{157} = 9,\!3325 \times 10^{157}$

Clever, nicht wahr?