Kreis Rechner

Dieser Kreis-Rechner hilft dir, den Umfang, den Durchmesser, den Flächeninhalt und den Radius eines beliebigen Kreises zu bestimmen.

Im folgenden Artikel findest du alle Kreisformeln, die du brauchst, um jeden dieser Werte zu berechnen. Lies weiter, wenn du nach der Kreisdefinition suchst oder verstehen möchtest, wie man den Mittelpunkt eines Kreises oder den Umfang eines Kreises findet — oder was Pi ist.

Außerdem findest du weiter unten Informationen über den Einheitskreis und die Eigenschaften eines Kreises sowie ein paar lustige Fakten über diese Form — wir verraten dir, welches das rundeste Land der Welt ist!

In diesem Rechner verwenden wir die folgende Notation:

• U steht für den Umfang,
• d für den Durchmesser,
• A für den Flächeninhalt, und
• r für den Radius des Kreises.

Du siehst lieber zu als zu lesen? Mit unserem Video lernst du in 90 Sekunden alles, was du brauchst:

Ein Kreis ist eine ebene, geschlossene Kurve, die aus allen Punkten des Kreises besteht, die sich in einer bestimmten Entfernung von einem bestimmten Punkt — dem Mittelpunkt — befinden. Alternativ kannst du den Kreis auch als die Menge aller Punkte definieren, die sich in der gleichen Entfernung von einem festen Punkt befinden. Der Name Kreis leitet sich aus dem Griechischen ab und bedeutet Reifen oder Ring.

Der Kreis ist technisch gesehen nur die Begrenzung und nicht der Flächeninhalt im Inneren der Form. Die gesamte Figur wird als Scheibe bezeichnet. Eine Scheibe kann geschlossen sein, wenn sie den Kreis enthält, der ihre Begrenzung darstellt, und offen, wenn sie das nicht tut. Im Alltagsgebrauch wird der Kreis manchmal als Scheibe verstanden — die ebene Oberfläche, die von einer solchen Kurve begrenzt wird.

Die Terminologie des Kreises besteht aus den Definitionen von:

• Umfang — die Entfernung um den Kreis;
• Radius — eine Linie, die den Mittelpunkt des Kreises mit einem beliebigen Punkt des Kreises verbindet;
• Durchmesser — eine Linie, die durch den Mittelpunkt verläuft und deren Endpunkte auf dem Kreis liegen; und
• Sehne — eine Linie, deren Endpunkte auf dem Kreis liegen.

Es gibt noch viele andere Begriffe, die mit dem Kreis in Verbindung gebracht werden, wie z. B. Bogen, Sekante oder Tangente, aber für unsere grundlegenden Erklärungen brauchst du nur die oben beschriebenen zu verstehen.

Ein Kreis hat eine einfache, unverwechselbare Form mit vielen ungewöhnlichen Eigenschaften:

• Er hat den größten Flächeninhalt für einen bestimmten Umfang;
• Er ist symmetrisch — Achsensymmetrie tritt für jede Gerade durch den Mittelpunkt auf, Punkt- und Rotationssymmetrie um den Mittelpunkt für jeden Winkel; und
• Er kann durch drei beliebige Punkte in der Ebene konstruiert werden (nicht alle auf derselben Geraden). Ein solcher Kreis ist ein eindeutig festgelegter.

Außerdem sind alle Kreise ähnlich, und eindeutige Kreise können den Umkreis oder den Inkreis eines Dreiecks bilden. Ein Kreis hat noch Dutzende anderer interessanter Eigenschaften, die du selbst entdecken kannst.

Die bekanntesten Gleichungen, die mit dem Kreis verbunden sind, sind:

1. Flächeninhalt des Kreises

   A = πr²

2. Umfang des Kreises

   U = 2πr

3. Kreisdurchmesser

   d = 2r

Aus den obigen Gleichungen kannst du viele weitere Kreisformeln ableiten, die du in den entsprechenden Abschnitten weiter unten findest.

Wenn du nach der Kreisformel selbst suchst, schau dir diesen Kreisgleichung Rechner 🇺🇸 an.

Der Einheitskreis ist ein Kreis mit einem Radius von eins. Normalerweise liegt sein Mittelpunkt im Ursprung (0, 0) des kartesischen Koordinatensystems.

Wählen wir einen beliebigen Punkt (x, y) auf dem Einheitskreis. Dann sind |x| und |y| die Längen der Schenkel des rechtwinkligen Dreiecks, wobei der Radius unseres Kreises die Hypotenuse der Länge 1 ist. Mithilfe des Satzes des Pythagoras können wir herausfinden, dass:

x² + y² = 1

Da x² = (-x)² ist, gilt die obige Gleichung für jeden Quadranten, nicht nur für den ersten.

Außerdem können wir die Schenkel des rechtwinkligen Dreiecks als Sinus und Kosinus definieren:

cos(α) = x / 1 = x

sin(α) = y / 1 = y

Dann:

sin²(α) + cos²(α) = 1

Diese Gleichung ist bekannt als trigonometrischer Pythagoras. Um Spannungen umzuwandeln, kannst du diese Identität auf den Mohrscher Spannungskreis Rechner 🇺🇸 anwenden.

U ist der Umfang des Kreises — also die Gesamtlänge der Linie, die du mit einem Zirkel einzeichnest. Du kannst ihn auf die folgenden Arten berechnen:

1. Wenn du den Radius oder Durchmesser des Kreises kennst:

   U = 2πr = πd

2. Wenn Radius und Durchmesser unbekannt sind, dann:

   U = 2√(πA)

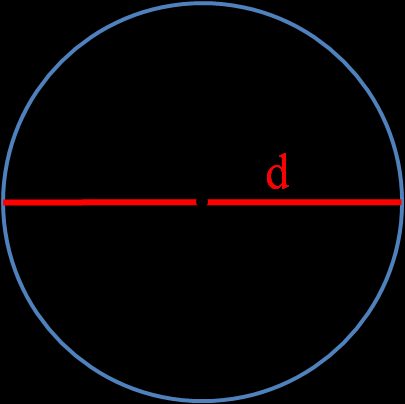
d ist der Durchmesser eines Kreises — die Länge einer Geraden, die durch den Mittelpunkt geht und zwei Punkte des Kreises verbindet. Du kannst ihn mit diesen Gleichungen bestimmen:

1. Wenn du den Radius des Kreises kennst:

   d = 2r

2. Wenn Radius und Flächeninhalt unbekannt sind:

   d = U / π

3. Wenn Radius und Umfang unbekannt sind:

   d = 2√(A / π)

A steht für den Flächeninhalt des Kreises. Er ist der einzige Wert, der in quadrierten Einheiten ausgedrückt wird (z. B. cm²). Du kannst ihn wie folgt berechnen:

1. Wenn du den Radius oder Durchmesser des Kreises kennst, lautet die Formel für den Flächeninhalt des Kreises:

   A = πr² = π × (d / 2)²

2. Wenn Radius und Durchmesser nicht bekannt sind, kannst du sie aus dem Umfang berechnen:

   A = U² / 4π

Wenn du dich für die Berechnung eines Bruchteils eines Kreises interessierst, sieh hier nach:

• Unser spezieller Flächeninhalt Halbkreis Rechner, um den Flächeninhalt eines Halbkreises zu ermitteln;
• Kreissektor Fläche Rechner, um den Flächeninhalt eines Pizzastücks zu ermitteln; oder
• Kreissegment Fläche Rechner 🇺🇸 — nützlich, wenn wir den Flächeninhalt des Querschnitts eines teilweise gefüllten Rohrs bestimmen möchten.

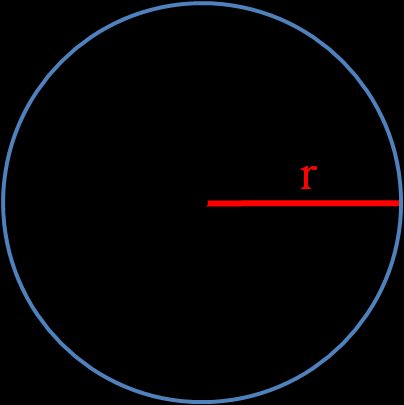
r — der Radius des Kreises ist die Länge der Geraden, die den Mittelpunkt mit einem beliebigen Punkt des Kreises verbindet. Du kannst ihn mit den folgenden Formeln ermitteln:

1. Wenn du den Durchmesser des Kreises kennst:

   r = d / 2

2. Wenn Durchmesser und Flächeninhalt unbekannt sind:

   r = U / 2π

3. Wenn Durchmesser und Umfang unbekannt sind:

   r = √(A / π)

Es gibt viele Möglichkeiten, den Mittelpunkt eines Kreises zu finden. Hier zeigen wir dir zwei konstruktive Methoden:

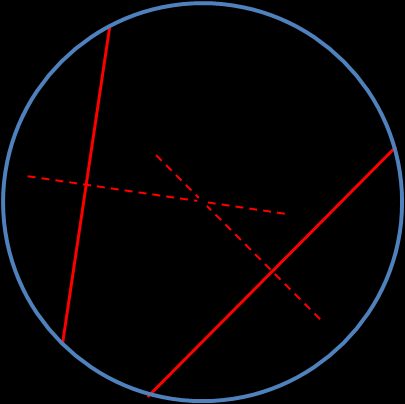
Methode 1 ist eine einfache Methode, um den Mittelpunkt eines Kreises mit einem Zirkel und einem Lineal zu bestimmen:

1. Benutze ein Lineal oder ein Geodreieck, zeichne zwei beliebige Sehnen.

2. Konstruiere die Mittelsenkrechte einer Sehne. Zeichne mit einem Zirkel zwei sich überschneidende Kreise (ihre Mittelpunkte liegen an den Endpunkten der Sehnen, der Radius ist gleich). Die Kreise werden sich in zwei Punkten schneiden — zeichne mit einem Lineal eine Gerade durch sie hindurch.

3. Wiederhole die Konstruktion der Winkelhalbierenden für die zweite Sehne.

4. Die beiden Winkelhalbierenden schneiden sich in einem Punkt; das ist der Mittelpunkt des Kreises.

Wenn du möchtest, kannst du die dritte Sehne und ihre Winkelhalbierende einzeichnen, um die Genauigkeit der Bestimmung des Mittelpunkts eines Kreises zu erhöhen und zu überprüfen.

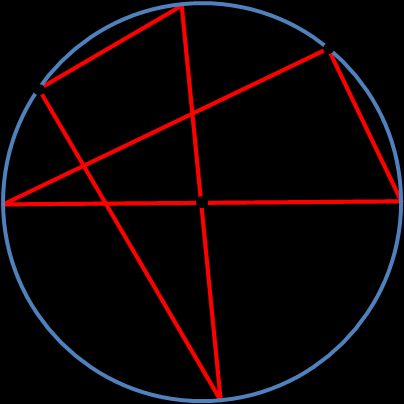
Methode 2 ist nur eine grobe Schätzung des Mittelpunkts eines Kreises, aber wenn du keine große Genauigkeit brauchst, kannst du diese Technik verwenden:

1. Wähle einen Punkt auf dem Kreis.

2. Nimm einen Gegenstand, der einen 90-Grad-Winkel und gerade Kanten hat. Das kann ein Geodreieck sein, aber auch alles, was du zur Hand hast — z. B. ein Buch, Karton oder ein Blatt Papier. Lege das Dreieck so, dass der rechte Winkel den von uns gewählten Punkt berührt.

3. Zeichne zwei senkrechte Geraden durch den Kreis. Markiere die Punkte, an denen sie sich mit dem Kreis schneiden.

4. Zeichne eine gerade Linie durch die Punkte. Das ist der Durchmesser des Kreises.

5. Du kannst den Mittelpunkt eines Kreises finden, indem du:

   • Die Winkelhalbierende des Durchmessers konstruierst (wie bei der ersten Methode); oder
   • Einfach das Verfahren wiederholst mit einen anderen Punkt auf dem Kreis. Ziehe senkrechte Geraden und erstelle einen weiteren Durchmesser. Der Schnittpunkt der beiden Durchmesser zeigt uns den Mittelpunkt des Kreises.

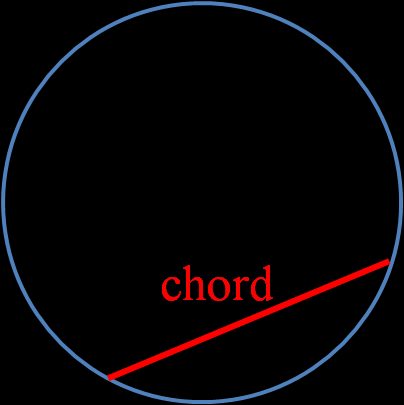
Eine Sehne ist ein Segment einer Geraden, die zwei Punkte auf einer beliebigen Kurve verbindet — diese Kurve kann ein Kreis sein, aber auch z. B. eine Ellipse. Wenn eine Kreissehne durch den Mittelpunkt eines Kreises verläuft, nennt man das den Durchmesser und ist die längste mögliche Sehne.

Die Kreissehne wurde in der antiken Trigonometrie häufig verwendet. Auch wenn wir sie durch trigonometrische Funktionen, insbesondere den Sinus, ersetzt haben, ist es immer noch gut zu wissen, wie man ihre Länge auf einem Einheitskreis berechnet:

Sehne(α) = √[(1 - cos(α))² + sin²(α)] = √[2 - 2cos(α)] = 2sin(α/2),

dabei ist α ein zentraler Winkel, der im positiven Sinne genommen wird und im Intervall 0 < α ≤ π liegen muss.

Wir können auch die Sehnenlänge eines Kreises beliebiger Größe bestimmen, indem wir die Sehne des Einheitskreises mit dem Radius r des Kreises multiplizieren, wie in der folgenden Gleichung dargestellt:

Sehne(α) = r × 2sin(α/2)

Konzentrische Kreise sind Kreise mit einem gemeinsamen Mittelpunkt. Der Bereich, der von zwei konzentrischen Kreisen mit unterschiedlichen Radien begrenzt wird, bildet einen Ring, den man als Anulus bezeichnet.

Was sind Beispiele für konzentrische Kreise im echten Leben?

• Die Zielscheibe beim Bogenschießen oder eine Dartscheibe.
• Kreisförmige Wellen auf dem Wasser.
• Wachstumsringe von Bäumen (näherungsweise).
• Die Rillen auf einer Schallplatte oder CD.

Pi ist die bekannteste mathematische Konstante. Sie beschreibt das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser:

π = Umfang / Durchmesser

Unabhängig von der Größe des Kreises ist das Verhältnis U/d konstant. Normalerweise wird die Pi-Konstante auf vier oder sechs Ziffern geschätzt. Die ersten 40 Dezimalstellen lauten:

π ≈ 3,1415926535897932384626433832795028841971...

π ist eine irrationale Zahl, was bedeutet, dass keine endliche Anzahl von Ziffern π genau darstellen kann (und sie sich nie wiederholen). Pi wurde mit über zweiundzwanzig Billionen Stellen hinter dem Komma berechnet, und diese Zahl steigt mit der Entwicklung der Computertechnologie weiter an.

Es gibt Wettbewerbe, bei denen die Teilnehmer versuchen, sich so viele Ziffern von Pi wie möglich zu merken. Der von Guinness World Records bestätigte Weltrekord liegt bei 70 000 Ziffern, während ein pensionierter japanischer Ingenieur einen inoffiziellen Rekord von über 100 000 Ziffern hält.

Wusstest du, dass...

• Es einen Schreibstil gibt, der Pilish genannt wird. Die Länge der aufeinanderfolgenden Wörter entspricht den Ziffern von Pi. Da Pi Einsen enthält, funktioniert dieser Schreibstil nur für Sprachen, in denen es Worte gibt, die aus nur einem Buchstaben bestehen, z. B. Englisch, Russisch oder Portugiesisch. Schaue dir beispielweise dieses Pilish in Englisch an:

  • May I have a large container of coffee beans – 314159265 in Pilish, wenn du dir 9 Stellen von Pi merken musst; und

  • How I need a drink, alcoholic in nature, after the heavy lectures involving quantum mechanics! – für die ersten 15 Stellen von Pi.

  Das ist eine hervorragende Methode, um sich die Pi-Stellen einzuprägen, denn das Gehirn kann sich Wörter viel besser merken als riesige Zahlenreihen. Vielleicht trainierst du deinen Geist und erfindest deine eigene Pilish-Geschichte?

• Es wurden bereits mehrere Bücher über die Pi-Konstante veröffentlicht. Darunter sind natürlich auch die üblichen mathematischen Aufsätze, sogar ganze Bücher wurden auf Pilish geschrieben! Das Buch mit dem Titel „Not A Wake: A Dream Embodying π's Digits Fully for 10 000 Decimals” von Mike Keith hält den Rekord für den längsten Pilish-Text mit 10 000 Ziffern.

• Es gibt einen Pi-Tag, der von vielen π-Enthusiasten gefeiert wird. Er findet am 14. März (3/14) statt. Vor ein paar Jahren, im Jahr 2015, gab es einen „besonderen" Pi-Tag, da die nächsten beiden Ziffern im Datum erschienen (3/14/15). Und die Uhrzeit — 9:26:53 — hat noch mehr Ziffern hinzugefügt! Wie kannst du diesen besonderen Geek-Tag feiern? Verkleide dich wie Albert Einstein (er hat am Pi-Tag Geburtstag) und iss den ganzen Tag kreisförmige Leckereien: von offensichtlichen Torten über Pfannkuchen bis hin zu fast perfekt runden Pizzen.

• Auch wenn es Spaß macht (?), π mit Hunderten oder Tausenden von Stellen zu lernen, wurde festgestellt, dass nur 38 Dezimalstellen ausreichen, um den Umfang des beobachtbaren Universums mit der Genauigkeit der Breite eines Wasserstoffatoms zu messen. Schau dir das Video über π und die Größe des Universums des Mathematikers James Grime auf dem Youtube-Kana Numberphile an.

Im alltäglichen Gebrauch ist die Quadratur des Kreises eine Metapher für das Kämpfen mit schwierigen oder sogar unmöglichen Aufgaben. Aber was bedeutet sie aus mathematischer Sicht?

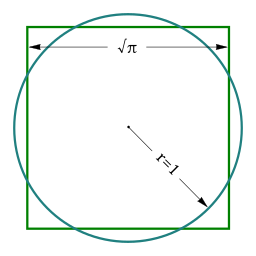
Dieses Problem beschäftigt die Mathematiker schon seit der Antike. Es ist die Aufgabe, ein Quadrat zu konstruieren, das den gleichen Flächeninhalt wie ein Kreis hat, aber nur mithilfe eines Lineals und eines Zirkels. Das Problem wurde 1882 als unlösbar erklärt, als der Mathematiker Lindemann zeigte, dass π eine transzendente Zahl ist; daher können π und √π nicht konstruiert werden. Wenn wir jedoch die Beschränkung durch Lineal und Zirkel aufheben, ist das Problem einfach und wurde bereits viele Male gelöst und beschrieben.

Die Wortkombination aus Quadrat und Kreis begegnet dir im Alltag: Box- und Wrestlingringe werden als quadrierte Kreise bezeichnet. Der Name kommt von der traditionellen Form eines Rings.

Ein Kreis ist eine zweidimensionale Form, die als Basis für einige gekrümmte geometrische dreidimensionale Formen dient.

Ein Zylinder hat zwei parallele (meist kreisförmige) Basen. Auch die Basis eines Kegels ist in den meisten Fällen ein Kreis.

Da wir die Formel für den Flächeninhalt eines Kreises kennen, können wir das Volumen solcher Formen leicht berechnen:

V(Zylinder) = πr²h

V(Kegel) = πr²h/3

Eine Kugel ist ein vollkommen rundes geometrisches Objekt im dreidimensionalen Raum, das die Oberfläche einer vollkommen runden Kugel darstellt. Sie ist vergleichbar mit dem Kreis und der Scheibe — nur eben in drei und nicht in zwei Dimensionen.

Es gibt auch den Begriff Kreis einer Kugel, und das ist ein Kreis, der auf einer Kugel liegt.

Ein Großkreis ist derjenige, dessen Ebene durch den Mittelpunkt der Kugel geht; jeder andere wird als Kleinkreis bezeichnet. Er wird z. B. in der Kartografie und Geografie verwendet — der Äquator ist der einzige Großkreis in der Familie der Breitengrade. Alle Längengrade bilden jedoch zusammen mit ihrem gegenüberliegenden Meridian einen Großkreis.

Wir können Länder auf viele Arten vergleichen — anhand ihres Flächeninhalts, ihrer Bevölkerung oder ihres Bruttoinlandsprodukts, aber hast du dich jemals gefragt, welches das rundeste Land der Welt ist?

Der Mathematiker und Blogger Gonzalo Ciruelos hat den Parameter Rundheit berechnet und die Rangliste erstellt. Der Gewinner in der Kategorie Rundheit ist Sierra Leone, während der Titel für das unrundeste Land der Welt an die Marshallinseln geht.

Sierra Leone steht auf Platz 1 der Rundheitsklassifizierung, aber es ist auch auf Platz 14 einer anderen Rangliste — das rechteckigste Land der Welt! Unfassbar, das Land mit der viertgrößten Rundheit — die Vatikanstadt — ist ebenfalls das Land mit der zweitgrößten Rechteckigkeit. Polen, das in der Klassifizierung der Rundheit auf Platz 5 steht, liegt in der Rangliste der Rechteckigkeit auf Platz 10. Wie ist es überhaupt möglich, gleichzeitig rechteckig und rund zu sein?!

Es geht um die Definition von Rechtwinkligkeit und Rundheit, die für komplexe oder verstreute Formen, sowie die Grenzen von Nationen, in der Regel nicht geeignet ist.

Eine bessere Erklärung und Diskussion der Ergebnisse findest du auf der bigthink-Website.

Wenn du dir immer noch nicht sicher bist, wie du unseren Kreisrechner nutzen kannst, dann schau dir diese Illustration an:

1. Nehmen wir an, wir möchten die Größe eines beispielhaften Kornkreises berechnen. Wir wählen einen, der von der Eulerschen Indentität inspiriert ist und 2010 in Wilton bei Marlborough, Großbritannien, gefunden wurde. Die Eulersche Identität ist ein Spezialfall der Eulerschen Formel (die sich aus dem Einheitskreis in der komplexen Ebene ableiten lässt).

2. Gib die angegebene Abmessung in den Kreis-Rechner ein. Wir wissen, dass der Kornkreis einen Durchmesser von etwa 91 m hatte. Wenn du die Einheiten ändern möchtest, klicke auf den Namen der Einheit und wähle die gewünschte Einheit aus einer Dropdown-Liste aus (in unserem Fall Meter).

3. Nun hast du alle Parameter des Kreises im Handumdrehen herausgefunden! Jetzt wissen wir, dass der:

   • Der Umfang eines Kreises ist gleich 285,885 m;
   • der Radius 45,5 m beträgt; und
   • Fläche ist 6503,9 m² — fast der Flächeninhalt eines Fußballfeldes! (Um genau zu sein: ≈91% des Flächeninhalts eines Fußballfeldes.)

Experimentiere mit dem Rechner und probiere es selbst aus. Wo wir gerade bei Kreisen sind: Wie groß ist der Umfang deines Rads?

Normalerweise bezeichnen wir mit U den Umfang eines Kreises, also die Entfernung um einen Kreis herum. Wenn du den Radius kennst, dann ist U gleich 2 π × Radius.

Ja, um den Umfang anhand des Durchmessers zu berechnen, kannst du die Formel U = π × Durchmesser verwenden. Das folgt aus der Tatsache, dass Durchmesser = 2 × Radius in die berühmte Formel U = 2π × Radius eingesetzt werden kann.

Um den Flächeninhalt eines Kreises anhand seines Umfangs zu bestimmen, gehst du folgendermaßen vor:

1. Quadriere den Umfang, d.h. berechne U².
2. Dividiere das Ergebnis durch 4π.
3. Das war's! Wir haben gerade die Formel A = U² / 4π angewendet, die den Flächeninhalt eines Kreises mit seinem Umfang verknüpft.

Die Antwort lautet 2√π ≈ 3,54. Das liegt daran, dass U² = 4π × Flächeninhalt ist. Wenn wir also die Quadratwurzel ziehen und Fläche = 1 einsetzen, erhalten wir U = √(4π × 1) = 2√π ≈ 3,54.