Es gibt eine beträchtliche Anzahl von Prozessen, für die du unseren Rechner für exponentielles Wachstum verwenden kannst. Als Faustregel wird die Formel für exponentielles Wachstum:
angewandt, wenn es eine Größe mit einem Anfangswert gibt, die sich im Laufe der Zeit mit einer konstanten Änderungsrate ändert. Die Basis der Exponentialfunktion in der obigen Formel ist .
Beachte, dass die Wachstumsrate, , eine beliebige positive Zahl sein kann; dieser Rechner funktioniert aber auch als Rechner für exponentiellen Zerfall – in dem Fall repräsentiert die Zerfallsrate, die zwischen 0 und -100 % liegen sollte. Sie kann nicht über 100 % liegen, da die Mengengröße nicht negativ sein kann.
Die Gleichung für exponentielles Wachstum wird bei der Radiokohlenstoffdatierung 🇺🇸, der Polymerase-Kettenreaktion, auch PCR genannt, (weshalb, erfährst du in unserem Annealing-Temperatur Rechner 🇺🇸) und bei der Berechnung von Zinseszinsen verwendet. Weitere Beispiele für die Anwendung dieser Formel findest du in den folgenden Abschnitten.
Wie berechnet man exponentielles Wachstum?
Betrachten wir nun das folgende Problem: Anfang 2019 betrug die Bevölkerung einer kleinen Stadt 10 000 Einwohner. Es wurde festgestellt, dass die Bevölkerung der Stadt jährlich mit einer konstanten Rate von 5 % wächst. Was solltest du tun, um die voraussichtliche Bevölkerungszahl im Jahr 2030 zu berechnen? Aus den vorgegebenen Daten wissen wir, dass die ursprüngliche Größe der Bevölkerung, , gleich 10 000 ist. Außerdem haben wir eine Wachstumsrate von .
Die Formel für exponentielles Wachstum lautet also:
Dabei ist t die Anzahl der Jahre, die seit 2019 vergangen sind. In unserem Fall, für das Jahr 2030, sollten wir einsetzen, da dies die Anzahl der Jahre zwischen 2030 und dem Ausgangsjahr 2019 ist. Wir erhalten also:
Die voraussichtliche Einwohnerzahl unserer kleinen Stadt im Jahr 2030 liegt also bei 17 103.
Falls du diese Formel etwas besser erforschen möchtest, kannst du unseren Rechner für exponentielles Wachstum dazu nutzen, die voraussichtliche Einwohnerzahl für jedes Jahr ab 2019 zu ermitteln. Aus der Berechnung ergibt sich folgende Tabelle, in welcher die Ergebnisse auf die nächste ganze Zahl gerundet wurden:
Jahr | ||
|---|---|---|
2019 | 0 | 10 000 |
2020 | 1 | 10 500 |
2021 | 2 | 11 025 |
2022 | 3 | 11 576 |
2023 | 4 | 12 155 |
2024 | 5 | 12 763 |
2025 | 6 | 13 401 |
2026 | 7 | 14 071 |
2027 | 8 | 14 775 |
2028 | 9 | 15 513 |
2029 | 10 | 16 289 |
2030 | 11 | 17 103 |
Wenn du ein besseres Gefühl für das Bevölkerungswachstum bekommen möchtest, kannst du diese Daten auch grafisch darstellen, wobei die horizontale Achse die Zeit und die vertikale Achse die Bevölkerungsgröße anzeigt. Die auf dem Graphen der stetigen exponentiellen Wachstumsfunktion liegenden Punkte sind nichts anderes als die Daten aus der Tabelle:
Da die Basis dieser Exponentialfunktion 1,05 und somit größer als 1 ist, ergibt sich ein exponentieller Wachstumsgraph, der ansteigt. Der Hauptunterschied zwischen diesem Graphen und dem normalen Graphen einer Exponentialfunktion ist, dass der y-Achsen-Schnittpunkt nicht 1, sondern 10 000 ist, was dem Anfangswert entspricht:
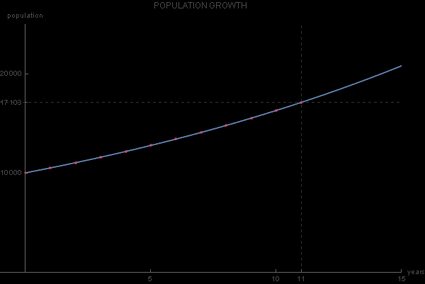
An diesem Beispiel sehen wir die möglichen Einschränkungen des exponentiellen Wachstumsmodells – es ist komplett unrealistisch, dass die Wachstumsrate im Laufe der Zeit konstant bleibt. Es ist nämlich kaum zu erwarten, dass die jährliche Wachstumsrate der Stadtbevölkerung über ein Jahrzehnt oder länger bei genau 5 % bleibt.
Im echten Leben schwankt die Wachstumsrate, was in diesem Modell des exponentiellen Wachstums nicht berücksichtigt wird. Ein realistischeres Modell des Bevölkerungswachstums ist das logistische Wachstumsmodell, welches die Tragfähigkeit mitberücksichtigt – eine Konstante, welche die natürliche Wachstumsgrenze der Bevölkerung wiedergibt.
So findest du den Zeitpunkt, an dem die Anfangsmenge eine bestimmte Größe erreicht
Bleiben wir weiterhin bei unserer kleinen Stadt, die nächste Frage, die du dir nun stellen könntest, wäre: „Wann können wir damit rechnen, dass die Einwohnerzahl einen entscheidenden Wert erreicht?“ Diese Informationen können durchaus nützlich sein, um z. B. die Stadtplanung an eine größere Bevölkerung anzupassen. Der Stadtrat will also wissen, in welchem Jahr man damit rechnen kann, dass sich die Einwohnerzahl der Stadt von ursprünglich 10 000 Einwohnern verdreifacht hat.
In dem Fall ist bekannt, wir kennen aber nicht den t-Wert. Lass es uns Schritt für Schritt berechnen:
-
Setze in die Formel ein: .
-
Nachdem wir beide Seiten der Gleichung durch 10 000 geteilt haben, erhalten wir: .
-
Berechne den Logarithmus zur Basis 1,05 für beide Seiten dieser Gleichung: .
-
Nachdem du den Logarithmus ausgerechnet hast, erhältst du: .
Die Antwort auf die Frage des Stadtrates lautet also: ca. 22 Jahre nach dem Ausgangsjahr 2019, also im Jahr 2041.
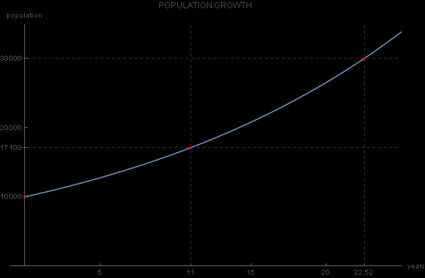
Kann Zeit negativ sein?
Vielleicht ist dir bereits ein gewisses Problem mit dem exponentiellen Wachstum und Zerfall aufgefallen, nämlich dass die Zeit eigentlich nur positive Werte annimmt, sodass wir eine zukünftige Größe voraussagen können. Wir können aber negative Zeitwerte in unsere Formel einsetzen und somit Werte für Zeitabschnitte vor dem Ausgangspunkt der Beobachtung berechnen.
Im Falle eines Bevölkerungswachstums kannst du dir folgende Frage stellen: wie viele Einwohner hatte unsere kleine Stadt im Jahr 2000, wenn wir davon ausgehen, dass die Bevölkerungswachstumsrate immer bei 5 % lag?
Um diese Frage zu beantworten, müssen wir also einsetzen, da das Jahr 2000 19 Jahre vor dem Jahr 2019 war. Die Antwort lautet also:
Einwohner, wie du auch auf diesem Graphen sehen kannst:
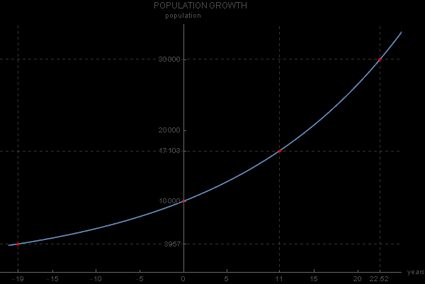
Eine alternative Schreibweise der Gleichung für exponentielles Wachstum
Für manche Anwendungen, zum Beispiel bei der Berechnung des exponentiellen Zerfalls einer radioaktiven Substanz, ist eine alternative Schreibweise der Formel für exponentielles Wachstum und Zerfall praktischer:
Der Koeffizient k ist ähnlich zu der Wachstumsrate r aus der ursprünglichen Formel für exponentielles Wachstum. Wenn du die obige Gleichung mit der ursprünglichen vergleichst, siehst du, dass die Beziehung zwischen und die folgende ist:
dies bedeutet:
und .
Beispiel für die Anwendung der Formel für exponentiellen Zerfall
Der radioaktive Zerfall ist ein bekanntes Beispiel für die Anwendung der Formel für exponentiellen Zerfall. Für eine bestimmte Anfangsmenge radioaktiver Substanz kannst du einfach die Formel aufschreiben, die den Zerfall im Laufe der Zeit berechnet. Ein interessanteres Beispiel ist, wie viel Kaffee um 22 Uhr noch in deinem Körper verbleibt, wenn du am Mittag eine Tasse Kaffee mit Koffein getrunken hast.
Wir basieren unsere Berechnung auf der Tatsache, dass die Halbwertszeit von Koffein im menschlichen Körper etwa sechs Stunden beträgt. Die Halbwertszeit ist die Zeit, die eine bestimmte Menge braucht, um auf die Hälfte ihres ursprünglichen Wertes zu sinken. In diesem Beispiel haben wir also:
In dem Fall ist es einfacher, die alternative Schreibweise der Formel für exponentielles Wachstum zu verwenden:
Und so berechnen wir es Schritt für Schritt:
-
Setze x(6)= 47,5 und t = 6 in die Gleichung ein: .
-
Nachdem du beide Seiten der Gleichung durch 95 geteilt und den natürlichen Logarithmus angewandt hast, ergibt sich: .
-
Wenn wir den natürlichen Logarithmus berechnen, erhalten wir: .
-
Die Formel für den exponentiellen Zerfall in unserem Beispiel lautet also: .
-
Da 22 Uhr zehn Stunden nach Mittag ist, wollen wir die Menge an Koffein zum Zeitpunkt t = 10 wissen. Dabei kommt folgendes heraus: .
Die Menge an Koffein, die um 22 Uhr in deinem Körper verbleibt, ist also ca. 30 mg.
Und wenn die Zeit nicht angegeben ist?
Die Zeit kann grundsätzlich in jeder geeigneten Einheit ausgedrückt werden. In manchen Fällen sind das Sekunden, in anderen Jahre. Du solltest die Zeiteinheit so wählen, dass sie der Art des beobachteten Prozesses entspricht. Wenn du zum Beispiel die Veränderung der Bevölkerungszahl einer Stadt verstehen willst, solltest du Jahre wählen. Wenn du hingegen die Menge an Kaffee berechnen willst, die in deinem Körper verbleibt, nachdem du eine Tasse getrunken hast, sollte die geeignete Zeiteinheit Stunden oder gegebenenfalls Minuten sein.
Beachte bitte, dass nicht zwingend als Zeiteinheit verwendet werden muss. In manchen Fällen kann die Variable, die die Veränderungsrate misst, eine andere als Zeit sein. Wenn du beispielsweise herausfinden möchtest, wie sich der Luftdruck mit der Höhe verändert, ist die Veränderung von der Distanz abhängig – du solltest somit z. B. Meter als Einheit wählen. Unser Rechner für den Luftdruck in Abhängigkeit der Höhe kann sich bei der Berechnung nützlich erweisen.
Wie sich unterschiedliche exponentielle Wachstumsraten auf das Wachstum auswirken
Der Unterschied in der Wachstumsrate r hat einen erheblichen Einfluss darauf, wie schnell sich die beobachtete Menge gegenüber dem Ausgangswert verändert. Fangen wir mit an und sehen wir uns mit dem Rechner für exponentielles Wachstum an, was sich für ergibt, wenn wir vier verschiedene Werte für einsetzen:
1% | 100 | 110,5 |
3% | 100 | 134,4 |
5% | 100 | 162,9 |
10% | 100 | 259,4 |
Wie wir in der Tabelle sehen, sind alle Anfangswerte gleich, ; die Endwerte von unterscheiden sich jedoch erheblich. Hierbei mag dich deine Intuition täuschen, denn der Unterschied zwischen 1 % und 3 % sieht nicht nach viel aus, aber nach zehn Zeitabschnitten ergibt sich ein um 21,67 % höherer Wert für beim 3%-igen Wachstum im Vergleich zum 1%-igen Wachstum.
Wenn du das 10%-ige Wachstum mit dem 5%-igen Wachstum vergleichst, wirst du einen noch größeren Unterschied feststellen, und zwar einen um 59,23 % größeren Wert als beim 10%-igen Wachstum. Du kannst diesen Unterschied anhand folgenden Darstellung der vier exponentiellen Wachstumsfunktionen beobachten:
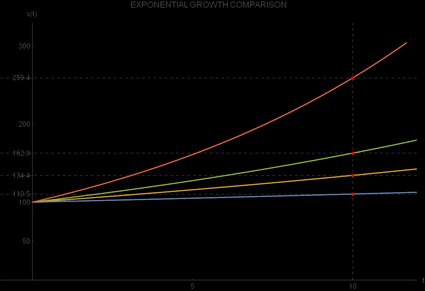
Welche Anwendungen hat das exponentielle Wachstum im echten Leben?
Die Formel für exponentielles Wachstum und Zerfall wird als Modell für verschiedene Phänomene verwendet, u. a. für:
- das Populationswachstum von Bakterien, Viren, Pflanzen, Tieren und Menschen;
- den Zerfall von radioaktivem Material;
- die Blutkonzentration von Medikamenten;
- den atmosphärischen Druck der Luft an einer bestimmten Höhe;
- den Zinseszins und Wirtschaftswachstum;
- die Radiokohlenstoffdatierung;
- die Rechenleistung von Computern, usw.
💡 Wusstest du schon, dass...
du mithilfe des bekannten Benfordschen Gesetzes überprüfen kannst, ob eine Reihe von Zahlen der Formel für exponentielles Wachstum folgt?
Referenzen
FAQs
Wie berechne ich exponentielles Wachstum?
Das exponentielle Wachstum wird durch die folgende Formel beschrieben:
Xt = X₀ ∙ (1 + r/100)ᵗ
dabei ist Xt die Menge zum Zeitpunkt t, X₀ der Anfangswert und r die Änderungsrate.
Was ist der Unterschied zwischen exponentiellem und linearem Wachstum?
Exponentielles Wachstum entsteht, indem der Anfangswert bei jedem Zeitschritt mit einem konstanten Faktor multipliziert wird. Lineares Wachstum bedeutet, dass zu dem Anfangswert bei jedem Zeitschritt der gleiche Wert addiert wird.
Wie berechne ich den exponentiellen Zerfall?
Der exponentielle Zerfall wird mit der folgenden Formel berechnet:
Xt = X₀ ∙ exp(μt)
dabei ist Xt die Menge zum Zeitpunkt t, X₀ die Ausgangsmenge und μ die Zerfallskonstante.