Tankvolumen Rechner

Mit diesem Tankvolumen-Rechner kannst du ganz einfach das Volumen deines Tanks bestimmen. Wähle zwischen zehn verschiedenen Tankformen: von normalen rechteckigen und zylindrischen Tanks bis hin zu Kapsel- und elliptischen Tanks. Du kannst sogar das Volumen eines Kegelstumpfes in Kegelbodentanks ermitteln. Gib einfach die Maße deines Tanks ein, und das Tool berechnet sein Gesamtvolumen für dich. Du kannst auch die Füllhöhe angeben, die zur Ermittlung des Füllvolumens verwendet wird.

Du fragst dich, wie das geht? Scrolle nach unten und du findest alle Formeln, die du brauchst – das Volumen eines Kapseltanks, eines elliptischen Tanks oder der weit verbreiteten Kegelbodentanks (manchmal auch konische Tanks genannt) und noch viele mehr!

Bist du auf der Suche nach anderen Arten von Tanks in anderen Formen und für andere Anwendungen? In unserem Volumen Rechner findest du das Volumen der gängigsten dreidimensionalen Körper. Wenn du etwas Spezielleres suchst, kannst du auch einen Blick auf den Aquarium Rechner und den Poolvolumen Rechner werfen, um Lösungen für alltägliche Volumenprobleme zu finden.

Dieser Tankvolumen-Rechner ist ein einfaches Werkzeug, das dir hilft, das Volumen des leeren Tanks sowie das Füllvolumen zu ermitteln. Du kannst zwischen zehn Tankformen wählen:

• Vertikaler Zylinder;
• Horizontaler Zylinder;
• Quader;
• Vertikale Kapsel;
• Horizontale Kapsel;
• Vertikales Oval (elliptisch);
• Horizontales Oval (elliptisch);
• Kegelbodentank;
• Kegelaufsatztank; und
• Frustum (Kegelstumpf, trichterförmig).

„Aber wie benutze ich diesen Tankvolumen-Rechner?”, magst du dich fragen. Schauen wir uns ein einfaches Beispiel an:

1. Entscheide dich für eine Form. Nehmen wir an, wir möchten das Volumen eines vertikalen Zylindertanks ermitteln – wähle diese Option aus der Dropdown-Liste. Der Rechner zeigt dir ein schematisches Bild des Tanks an; vergewissere dich, dass es das ist, was du möchtest!

2. Gib die Abmessungen des Tanks ein. In unserem Fall müssen wir die Höhe und den Durchmesser eingeben. Nehmen wir eine Höhe von $32\ \mathrm{cm}$ und einen Durchmesser $24\ \mathrm{cm}$ an. Außerdem können wir die Füllhöhe eingeben – $28\ \mathrm{cm}$.

3. Der Tankvolumen-Rechner hat bereits das Gesamt- und Füllvolumen ermittelt! Das Gesamtvolumen des Tanks ist $14,\!48\ \mathrm{l}$, und das Füllvolumen beträgt $12,\!67\ \mathrm{l}$. Wie immer kannst du die Einheiten ändern, indem du auf die Volumeneinheiten selbst klickst. Easy-peasy!

Um das Gesamtvolumen eines zylindrischen Tanks zu berechnen, brauchen wir nur den Zylinderdurchmesser (oder Radius) und die Höhe des Zylinders (die auch als Länge bezeichnet werden kann, wenn er waagerecht liegt).

Vertikaler Zylindertank

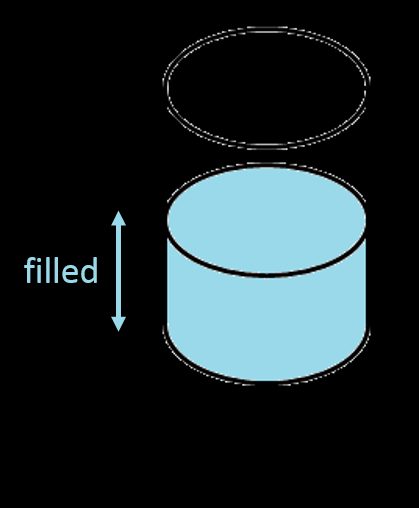
Wir können das Gesamtvolumen eines zylindrischen Tanks mit der Standardformel für das Volumen ermitteln – die Grundfläche multipliziert mit der Höhe. Die Grundfläche ist ein Kreis, also ist seine Fläche nach der bekannten Gleichung gleich $\pi \times \mathrm{Radius}^2$. Daher sieht die Formel für das Volumen eines vertikalen Zylindertanks wie folgt aus:

wobei:

• $r$ — der Radius der Grundfläche ist; und
• $h$ — die Höhe des Zylinders ist.

Wenn wir das Füllvolumen berechnen möchten, müssen wir das Volumen eines „kürzeren“ Zylinders ermitteln – so einfach ist das!

dabei ist $f$ die Höhe des gefüllten Teils des Zylinders.

Horizontaler Zylindertank

Das Gesamtvolumen eines waagerechten zylindrischen Tanks kann auf analoge Weise ermittelt werden – es ist die Fläche des kreisförmigen Endes mal der Länge des Zylinders:

dabei ist $l$ die Länge des Zylinders.

Komplizierter wird es, wenn wir das Füllvolumen des horizontalen Zylinders ermitteln möchten. Zuerst müssen wir die Grundfläche ermitteln: die Fläche des Kreissegments, das von der Flüssigkeit bedeckt ist:

dabei ist $r$ der Radius der Grundfläche und $\theta$ ist der Zentralwinkel des Segments. Der Winkel $\theta$ lässt sich mit dem Kosinus ermitteln:

dabei ist $f$ die Höhe des gefüllten Abschnitts der Grundfläche.

Deshalb:

Die Formel für das Volumen eines teilweise gefüllten horizontalen Zylinders $V_{\scriptsize{\mathrm{hz}}}$ lautet schließlich:

wobei:

Wenn der Tank mehr als halb voll ist, ist es einfacher, den leeren Teil vom Gesamtvolumen abzuziehen.

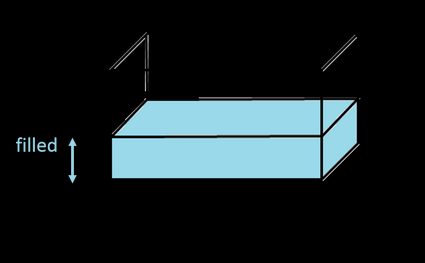
Wenn du dich fragst, wie man das Volumen eines Quadertanks (auch bekannt als Box oder rechteckiges Hexaeder) berechnet, bist du hier genau richtig! Du kennst diesen Tank vielleicht als rechteckigen Tank – aber das ist nicht sein richtiger Name, denn ein Rechteck ist eine zweidimensionale Form und hat daher kein Volumen.

Um das Volumen eines Quaders zu ermitteln, multiplizierst du alle Maße des Tanks:

wo:

• $h$ — die Höhe des Tanks ist;
• $b$ — die Breite ist; und
• $l$ — die Länge des Tanks ist.

Wenn du wissen möchtest, wie groß das Füllvolumen in einem Tank ist, änderst du einfach die Variable Höhe in den Füllstand in der Volumen-Formel. Das Volumen eines gefüllten Quaders, $V_{\scriptsize{\mathrm{QuaderFV}}}$, ist:

wobei $f$ die Höhe des gefüllten Teils ist.

Für diesen Tankvolumen-Rechner spielt es keine Rolle, ob der Tank horizontal oder vertikal aufgestellt ist. Achte nur darauf, dass Gefüllt und Höhe auf der gleichen Achse liegen.

Unser Tool definiert eine Kapsel als zwei Halbkugeln, die durch einen Zylinder getrennt sind. Um das Gesamtvolumen einer Kapsel zu berechnen, musst du nur das Volumen der Kugel zum Zylinderteil addieren:

Je nach Position des Tanks unterscheiden sich die Berechnungen des Füllvolumens ein wenig:

1. Für liegende Kapseltanks

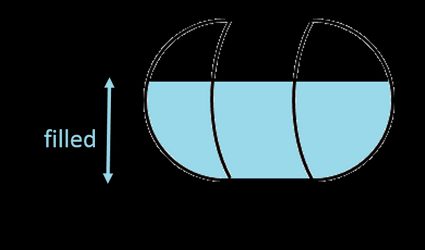
Da die Halbkugeln an beiden Enden des Tanks identisch sind, bilden sie eine kugelförmige Kappe – addiere diesen Teil $V_{\scriptsize{\mathrm{Kugel}}}$ zu dem Teil aus dem horizontalen Zylinder $V_{\scriptsize{\mathrm{hz}}}$ (siehe Absatz oben), um das Volumen der Flüssigkeit in einer gefüllten horizontalen Kapsel zu berechnen ($V_{\scriptsize{\mathrm{Kapsel}}}$):

wobei:

• $d$ — der Durchmesser des Tanks ist;
• $f$ — die Füllhöhe ist; und
• $\theta$ — der Winkel ist, der dem gefüllten Teil im Zylindertank entspricht.

2. Für vertikale Kapseltanks

Die Formel unterscheidet sich für verschiedene Füllhöhen. In allen folgenden Formeln werden wir diese Größen treffen:

• $d$ — Durchmesser des Tanks;

• $f$ — Füllhöhe der Flüssigkeit; und

• $l$ — Länge des zylindrischen Abschnitts.

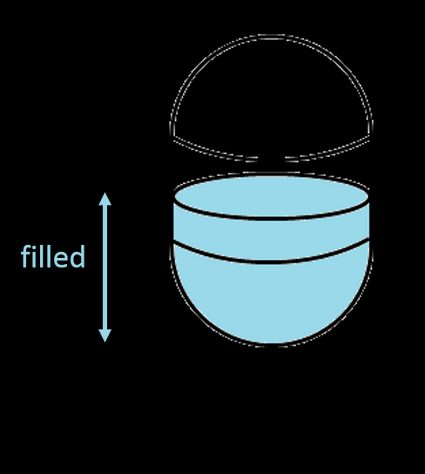
• Wenn $f < d/2$, dann befindet sich die Flüssigkeit nur im unteren Teil der Halbkugel, also brauchen wir nur die Formel für das Volumen einer kugelförmigen Kappe:

• Wenn $d/2 < f < d/2 +l$, dann müssen wir das Volumen der Halbkugel und des „kürzeren” Zylinders addieren:

• Wenn $d/2 + l < f$, bedeutet das, dass wir eine volle untere Halbkugel und einen vollen Zylinder haben, also müssen wir nur die Kugelhaube (leerer Teil) vom Gesamtvolumen abziehen:

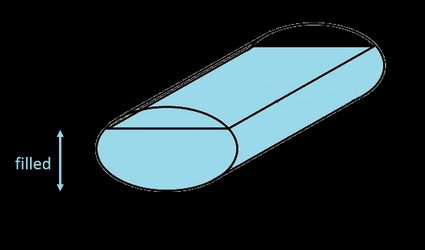
In unserem Rechner definieren wir einen ovalen Tank als einen zylindrischen Tank mit einem elliptischen Ende. Um das Gesamtvolumen eines elliptischen Tanks zu ermitteln, musst du die Ellipsenfläche mit der Länge des Tanks multiplizieren:

wobei:

• $b$ — die Breite des Tanks ist;
• $h$ — die Höhe des Tanks ist; und
• $l$ — die Länge des Tanks ist.

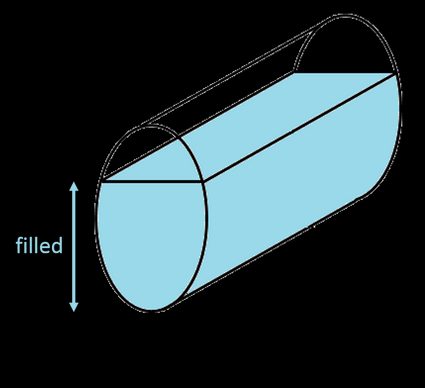
Endlich wieder eine einfache Formel! Leider ist die Ermittlung des Volumens eines teilweise gefüllten Tanks – sowohl in horizontaler als auch in vertikaler Position – nicht so einfach. Du musst die Formel für die Fläche des Ellipsensegments verwenden und das Ergebnis mit der Länge des Tanks multiplizieren:

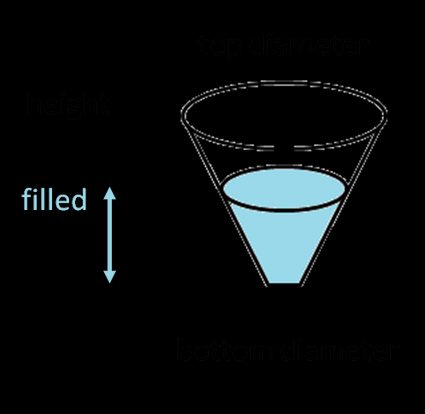
Um das Volumen des Kegelstumpfes zu berechnen (eine besondere Form, die wir in unserem Kegelstumpf Rechner 🇺🇸 genauer untersuchen), verwende die Formel:

wobei:

• $d_{\mathrm{Oben}}$ — der oberer Durchmesser des Kegelstumpfes ist;
• $d_{\mathrm{Unten}}$ — der unterer Durchmesser des Kegelstumpfes ist;
• $h_{\mathrm{Kegel}}$ — die Höhe des Tanks ist.

Wenn du das Kegelstumpfvolumen für eine bestimmte Füllhöhe ermitteln möchtest, berechne zuerst den oberen Radius des gefüllten Teils:

wobei:

(Du kannst die Formel aus der Ähnlichkeit der Dreiecke ableiten)

Danach musst du nur noch das Volumen des neuen Kegelstumpfes ermitteln:

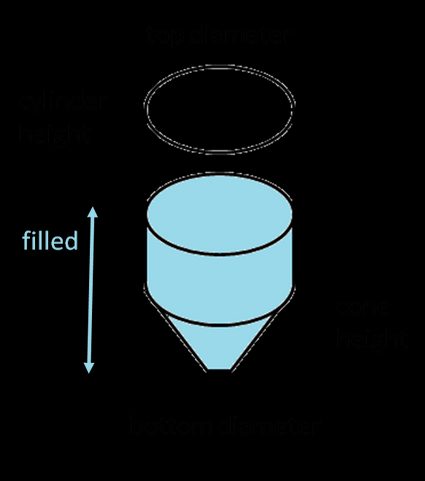
Das Gesamtvolumen eines Kegelbodentanks zu ermitteln, ist gar nicht so schwer – addiere einfach das Volumen des kegelförmigen Teils zum Volumen des zylindrischen Teils:

wobei:

• $d_{\mathrm{Oben}}$ — der obere Durchmesser des Kegelstumpfes ist;
• $d_{\mathrm{Unten}}$ — der untere Durchmesser des Kegelstumpfes ist;
• $h_{\mathrm{Kegel}}$ und $h_{\mathrm{Zylinder}}$ — die Höhen der beiden Tanks sind.

Um die Füllhöhe zu berechnen, musst du nur den Kegelstumpfteil und den Zylinderteil, je nach Füllstand der Flüssigkeit, mithilfe der obigen Gleichungen addieren.

Die Berechnung des Gesamtvolumens des Tanks mit Kegelstumpf ist genau dasselbe wie die des Tanks mit Kegelboden. Der einzige Unterschied besteht darin, dass du den gefüllten Teil ermitteln möchtest – natürlich wird zuerst der zylindrische Teil gefüllt und erst dann der Kegelstumpf.