Steigungsgrad Rechner

Dieser Steigungsgrad-Rechner bestimmt die Steigung einer Erdoberfläche und drückt diese auf vier verschiedene Arten aus. Die Steigung kann als Höhenwinkel gegenüber der horizontalen Ebene, als prozentuale Abweichung von der horizontalen Gerade, als Verhältnis der Steigung zum Streckenverlauf oder als Steigungseinheit zum Streckenverlauf angegeben werden. Um die Steigung einer Geraden zu berechnen und mehr über Steigungen im Allgemeinen zu erfahren, kannst du dir unseren Steigung Rechner anschauen. Wenn du mehr darüber erfahren möchtest, wie du den Steigungsgrad bestimmen kannst, lies weiter.

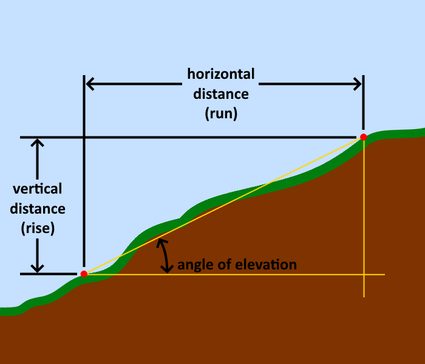
Der Steigungsgrad (oder die Steilheit) ist der Grad der Neigung eines bestimmten Geländestücks. Dabei kann es sich einfach um die Steilheit zwischen zwei bestimmten Punkten in einem bestimmten Gebiet handeln, um den Durchschnitt der allmählichen Veränderung der Steilheit eines Gebiets oder um eine sprunghafte Veränderung der Höhe des Bodens. Normalerweise messen wir die Höhe des Bodens als Höhe über dem Meeresspiegel.

Die Kenntnis der Höhenlage eines Gebiets bietet viele Vorteile und kann eine Voraussetzung für z. B. Bauarbeiten oder Bewässerungsanlagen sein. Hier sind einige Beispiele, für welche die Kenntnis der Höhenlage eine wichtige Rolle spielt:

• Beim Straßenbau — wir verwenden sie zum Beispiel in der vertikalen Kurvenformel 🇺🇸. In sehr steilem Gelände werden Serpentinen angelegt, um einen sicheren Auf- und Abstieg zu gewährleisten. Bei weniger steilem Gelände können Ingenieure ein Abtragungs- und Auffüllungssystem entwerfen, um das Gefälle zu verringern. Dabei wird die Erde vom oberen Teil des Hangs auf den unteren Teil abgetragen.
• Beim Bau von Stützmauern — sie stützen das Erdreich über ihnen, damit es nicht bergab erodiert. Eine Stützmauer kann gegen eine Klippe gebaut werden, um Erdrutschen zu verhindern.
• Beurteilung der Tragfähigkeit eines Bauwerks — wenn du ein Bauwerk auf einem abschüssigen Gelände errichten möchtest, brauchst du unter Umständen ein zusätzliches Fundament.
• Die Bestimmung der Kraft des Wasserflusses — aus höheren Lagen ist dies wichtig, um festzustellen, ob das Land im Tal ohne Pumpen bewässert werden kann.
• und noch vieles mehr :)

Wir berechnen die Geländesteigung auf die gleiche Weise, wie wir die Steigung einer Geraden berechnen. Für die Steigung einer bestimmten Gerade werden die Koordinaten ihrer Endpunkte benötigt. Die Steigung ist der Quotient aus der Änderung der Werte von x und y in Anhängigkeit voneinander. Als Gleichung sieht das so aus:

Die Veränderung des y-Wertes ist der Anstieg, da sie entlang der vertikalen Achse verläuft. Die Veränderung der x-Werte ist die Strecke, da sie entlang der horizontalen Achse verläuft. Aus dieser Beziehung ergibt sich die Gleichung: Steigung = Anstieg über die Strecke 🇺🇸 oder:

Wir können die Steigung auch in Form von Winkeln ausdrücken, indem wir die trigonometrischen Funktionen anwenden. Wir interessieren uns für den Winkel zwischen der horizontalen Ebene und der Ebene der Steigung. Einen Winkel, der von der Horizontalen nach oben geht, nennen wir Höhenwinkel, während derjenige, der nach unten gehen, die Neigungswinkel sind. Wir können diesen Winkel mit der Arctan-Funktion, der Umkehrfunktion des Tangens, bestimmen. Als Gleichung sieht das wie folgt aus:

Wenn du keinen Taschenrechner mit dieser trigonometrischen Funktion hast, keine Sorge, wir haben dies bereits in unseren Steigungsgrad-Rechner integriert. Wenn du mehr über die anderen wichtigen trigonometrischen Funktionen erfahren möchtest, kannst du in unserem Trigonometrische Funktionen Rechner 🇺🇸 mit den Winkeln experimentieren.

Wir können die Steigung nicht nur mithilfe von Verhältnissen und Winkeln ausdrücken, sondern auch in Prozenten — dazu müssen wir nur ihr Verhältnis mit 100 multiplizieren, woraus sich die untenstehende Gleichung ergibt. Ein Gefälle von hundert Prozent bedeutet, dass die Steigung des Hangs gleich der Gefällstrecke ist. Die sich daraus ergebende Neigung ist weder sehr steil noch flach, sondern eine durchschnittliche Neigung. Hier siehst du die Gleichung:

Wir haben unseren Steigungsgrad-Rechner mit all diesen Gleichungen ausgestattet, sodass er dir jedes Mal, wenn du einen Wert für eine Variable eingibst, alle anderen Variablen berechnet. Du kannst die Steigung festlegen und die horizontale Strecke bestimmen, die erforderlich ist, um die gewünschte Änderung einer vertikalen Strecke zu erhalten, sowie den Höhenwinkel ermitteln.

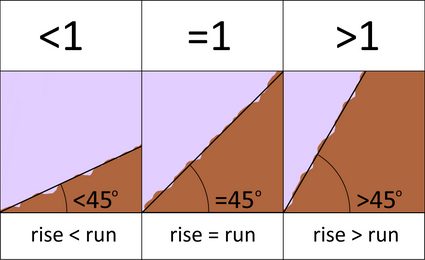
Steigungswerte sind ziemlich einfach zu verstehen. Geländeniveaus unter 1 ( <1) bedeuten eine schwache Steigung (Anstieg < Strecke). Geländeniveaus größer 1 (>1) bedeuten, dass das Gelände steil ist (Anstieg > Strecke). Was den Höhenwinkel angeht, so sind Winkel über 45 Grad steil, während Winkel unter 45 Grad relativ flach sind.

Wir können die Strecke, also die Veränderung der horizontalen Entfernung, mit einem straff gezogenen Maßband ermitteln.

Die vertikale Entfernung kann mit optischen Geräten wie einem Vermessungstransit mit Nivellierlatte ermitteln werden. Ein Vermessungstransit hat ein eingebautes Fernrohr, das über ein Stativ seitlich oder vertikal gedreht werden kann. Wenn du es auf die Nivellierlatte (die wie ein großes Lineal aussieht) richtest, erhältst du einen Messwert. Diesen Wert können wir in die Höhe zwischen der Nivellierlatte und dem Transit umrechnen. Der Transit eines Vermessungsingenieurs hat außerdem besondere Markierungen auf seinem Blickfeld, mit denen er, in Verbindung mit einer Nivellierlatte, auch horizontale Entfernungen messen kann.

Wir können als Hilfsmittel auch einen Neigungsmesser verwenden, der direkt den Höhenwinkel zwischen zwei Punkten angibt. Ein Neigungsmesser ist wie ein Mini-Teleskop, an dessen Seite ein Winkelmesser angebracht ist. Andere, ausgefeilte digitale Geräte können dabei helfen, die Neigung einer bestimmten Fläche zu ermitteln. Ein Smartphone kann, wenn es mit geeigneter Hardware wie Gyroskopiesensoren ausgestattet ist, genau die Neigung einer Fläche bestimmen, wenn es auf dieser Fläche liegt.

Wir können die Durchschnittswerte der Geländeniveaus aufzeichnen, um eine Höhenlinienkarte zu erstellen. Eine Höhenlinienkarte ist eine topografische Karte, die dem Betrachter einen Überblick über die Beschaffenheit des Geländes in einem bestimmten Gebiet gibt. Eine vertikale Überhöhung ist oft notwendig, um bestimmte Geländemerkmale wie die Höhe von Bergen oder Vulkanen hervorzuheben.

Mehr darüber erfährst du in unserem Vertikale Überhöhung Rechner 🇺🇸.

Die Baldwin Street in Neuseeland hat ein beeindruckendes Gefälle von etwa 0,35, was einer horizontalen Länge von 2,86 m pro Höhenmeter entspricht. Die kurze, 350 m lange Straße ist eine echte Herausforderung!

Eine Steigung von 0,35 entspricht einem Winkel von:
Winkel = arctan(Anstieg / Strecke) = arctan(1/2,86) = 19,27°.

Die Formel gibt die Steigung als Winkel an:
Steigung (Winkel) = arctan(Anstieg / Strecke)
Dabei ist der Anstieg die vertikale Entfernung und die Strecke die horizontale Entfernung einer Neigung.
Um die Steigung in Prozent zu berechnen, nimmst du das Argument der Arkustangens-Funktion und multiplizierst es mit 100:
Steigung (in Prozent) = Anstieg / Strecke × 100.

Eher widersinnig ist, dass eine Steigung von 100% einem Winkel von 45° entspricht. Bedenke aber, dass die Steigung das Ergebnis der Gleichung ist:
Steigung = Anstieg / Strecke,
wobei:

• Anstieg – die vertikale Strecke ist und
• Strecke – die horizontale Strecke ist.

Eine Steigung, bei der jeder horizontale Meter einem vertikalen Meter entspricht, hat die Steigung 1, was multipliziert mit 100 den Wert 100% ergibt.

Nehmen wir an, die Straße hat eine Steigung von 12 Metern pro 200 Meter Strecke. Die Steigung würde dann 0,06 betragen. So berechnest du die Steigung einer Straße mit:

• Anstieg = 12 m und
• Strecke = 200 m:

1. Berechne das Verhältnis zwischen Anstieg und Strecke:
   Steigung = Anstieg / Strecke = 12/200 = 0,06.
2. Wenn du den Winkel der Steigung wissen möchtest, berechne den Arkustangens der Werte:
   Steigung (Winkel) = arctan(Anstieg / Strecke) = arctan(12/200) = 3,43°.
3. Wenn du die Steigung als Prozentsatz wissen möchtest, multipliziere das Verhältnis mit 100:
   Steigung (Prozentsatz) = 100 × Anstieg / Strecke = 6%.