Calculadora de Ponto Flutuante

A calculadora de ponto flutuante da Omni está aqui para ajudar você a entender o padrão IEEE754. Ela atua como um conversor para números de ponto flutuante. Ela converte números flutuantes de 32 bits e 64 bits de representações binárias para números decimais reais e vice-versa.

Antes de entrarmos nos bits e bytes dos formatos de números float32 e float64, vamos aprender como funciona a calculadora de ponto flutuante. Basta que você siga estes passos simples:

1. Se você quiser converter a codificação binária de um número de ponto flutuante para o número decimal que ele representa, selecione ponto flutuante para número na parte superior da calculadora. Em seguida:

   • Selecione a precisão usada. Isso determina como sua representação binária será interpretada.

   • Digite os dígitos binários do número de ponto flutuante. Você pode inserir o sinal, o expoente e a fração separadamente, ou pode inserir toda a cadeia de bits de uma só vez. Selecione sua preferência no menu suspenso método de entrada de bits.

   • O valor armazenado em seu float será mostrado na parte inferior da calculadora.

2. Se você quiser converter um valor em sua representação de ponto flutuante, selecione número para ponto flutuante na parte superior da calculadora. Em seguida:

   • Digite o número no próximo campo.

   • As representações binárias e hexadecimais do ponto flutuante IEEE754 de precisão simples e dupla serão mostradas abaixo.

   • A calculadora de ponto flutuante também mostrará a você o valor real armazenado devido à perda de precisão inerente ao formato de ponto flutuante. O erro devido a essa perda de precisão também será relatado.

Na computação, um número de ponto flutuante é um formato de dados usado para armazenar números fracionários em uma máquina digital. Um número de ponto flutuante é representado por uma série de bits (1 e 0). Os computadores realizam operações matemáticas usando esses bits, reproduzindo operações que fazemos com números decimais. Quando um ser humano deseja ler o número de ponto flutuante, uma fórmula complexa reconstrói os bits no sistema decimal.

O padrão IEEE754 (estabelecido em 1985 pelo Instituto de Engenheiros Elétricos e Eletrônicos) padronizou o formato de ponto flutuante e também definiu como o formato pode ser operado para executar cálculos matemáticos e outras tarefas. Ele foi amplamente adotado por projetistas de hardware e software e se tornou o padrão para representar números de ponto flutuante em computadores. Quando alguém menciona “números de ponto flutuante” no contexto da computação, geralmente se refere ao formato de dados IEEE754.

O formato de ponto flutuante IEEE754 mais conhecido (precisão simples, ou “32 bits”) é usado em quase todos os aplicativos de computadores modernos. O formato é altamente flexível: o float32 pode codificar números tão pequenos quanto 1,4×10^-45 e tão grandes quanto 3,4×10³⁸ (positivos e negativos).

Além do formato de precisão simples, o padrão IEEE754 também codifica a precisão dupla (“64 bits” ou float64), que pode armazenar números de 5×10^-324 a 1,7×10³⁰⁸. Os formatos IEEE754 menos usados incluem:

• Meia precisão (“16 bits”);
• Precisão quádrupla (“128 bits”); e
• Precisão óctupla (“256-bit”).

No entanto, um número de ponto flutuante não é simplesmente um número conversor integrado ao sistema de números binários; ele é muito mais complicado do que isso! Vamos aprender como funciona o padrão de ponto flutuante IEEE754.

Qualquer representação binária de ponto flutuante consiste em três segmentos de bits: sinal, expoente e fração.

• O sinal (S) indica se o número é positivo ou negativo;
• O exponente (E) eleva 2 a alguma potência para escalonar o número; e
• A fração (F) determina os dígitos exatos do número.

Os comprimentos dos segmentos e a fórmula exata aplicada a S, E e F para recriar o número dependem da precisão do formato.

Quando armazenados na memória, $S$, $E$ e $F$ são colocados de ponta a ponta para criar a representação binária completa do número de ponto flutuante. Na memória do computador, ele pode ter a seguinte aparência:

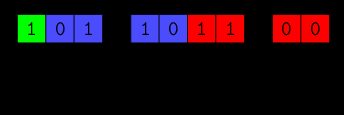
Esses bits são o que o computador manipula quando a aritmética e outras operações são realizadas. O computador nunca vê um número como seus dígitos decimais, ele só vê e trabalha com esses bits.

Vejamos em mais detalhes os dois formatos de ponto flutuante mais comuns: float32 e float64.

O float32 é o formato IEEE754 mais comumente usado. Conforme sugerido pelo termo “32-bit float”, sua representação binária subjacente tem 32 bits de comprimento. Eles são segmentados da seguinte forma:

• 1 bit para o sinal ($S$);
• 8 bits para o expoente ($E$); e
• 23 bits para a fração ($F$).

Quando armazenados na memória, os bits têm a seguinte aparência:

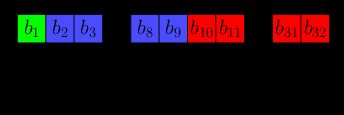
Podemos reescrevê-lo como uma cadeia de caracteres (string) binária:

O valor real que esse float de 32 bits armazena pode ser calculado da seguinte forma:

onde:

• $127$ é chamado de desvio de expoente e é inerente ao formato de precisão simples;
• $x_2$ significa que $x$ deve ser interpretado como se estivesse na base 2 ou binária; e
• $(1.b_{10}...b_{32})_2$ significa que você deve pegar os bits binários $b_{10}$ a $b_{32}$ e usá-los como a parte fracionária de $1$ para formar uma fração binária. Consulte nosso conversor de frações binárias 🇺🇸 para obter ajuda sobre esse tópico.

Você pode reescrever melhor a fórmula usando $S$, $E$ e $F$, ou seja:

onde:

• $S = b_1$;
• $E = (b_2\ ...\ b_9)_2$; e
• $F = (b_{10}\ ...\ b_{32})_2$.

Para permitir que os formatos de ponto flutuante armazenem números realmente pequenos com alta precisão, $E=0$ e $F>0$ devem ser aplicados a uma outra fórmula. Para o float32, essa fórmula é:

Os números criados por essa fórmula são chamados de “números subnormais”, enquanto os “números normais” são criados usando a fórmula anterior.

Há outros casos especiais, codificados por valores específicos para $E$ e $F$:

$\text{NaN}$ significa “não é um número” (Not a Number em inglês), que é retornado quando você divide por zero ou realiza cálculos impossíveis usando o infinito. Nos casos de $\pm 0$ e $\pm \infty$, o bit de sinal determina se o número é positivo ou negativo. E sim, o zero negativo existe!

Um exemplo

Vamos converter a representação binária de ponto flutuante 01000001110111100000000000000000 para o número real que ela representa.

1. Primeiro, vamos segmentá-lo em $S$, $E$ e $F$:

   • $S = 0_2 = 0$

   • $E = 10000011_2 = 131$

   • $F = 10111100000000000000000_2$

2. Como $0<E<255$, usamos a fórmula do número normal:

   $(-1)^S \times 2^{E-127} \times (1.F)_2$

   • $(-1)^S = 1$ (portanto, o número é positivo!)

   • $2^{E-127} = 2^{4} = 16$

   • $(1.F)_2 = 1.101111_2 = 1{,}734375$

3. Combine os três números através de uma multiplicação:

   $1 \cdot 16 \cdot 1{,}734375 = \textbf{27,75}$

Quer ver com seus próprios olhos? Experimente esse valor em nossa calculadora de ponto flutuante para que você a veja em ação!

Observe que $01000001110111100000000000000000_2$ convertido diretamente de binário para decimal não é $27{,}75$, mas $1.\!105.\!068.\!032$. Uma grande diferença, você não acha?

Os funcionamentos internos do tipo de dados float64 são muito parecidos com os do float32. As principais diferenças entres esses dois floats são:

• Os comprimentos dos segmentos de expoente e fração da representação binária: em floats de 64 bits, $E$ ocupa 11 bits e $F$ ocupa 52.
• O desvio de expoente: em floats de 64 bits, é 1023 (enquanto em floats de 32 bits, é 127).

As fórmulas para a reconstrução de pontos flutuantes normais e subnormais de 64 bits são, portanto, respectivamente:

e

Devido aos bits adicionais de expoente e fração em comparação com o float32, o float64 pode armazenar números muito maiores e com precisão muito maior.

Para converter um número decimal em uma representação de ponto flutuante, siga estas etapas:

1. Converta o número inteiro para binário e, em seguida, normalize-o, ou seja, escreva-o em notação científica usando a base 2.
2. Trunque a fração após o ponto decimal para o comprimento de fração permitido.
3. Extraia o sinal, o expoente e os segmentos da fração.

Consulte o padrão IEEE754 para obter instruções mais detalhadas.

Um exemplo

Vamos converter $27{,}75$ de volta à sua representação de ponto flutuante.

1. Nossa parte inteira é $27$, que em binário é $11011_2$. Nossa parte fracionária é $0{,}75$. Vamos convertê-la em uma fração binária:

   • $0{,}75 \cdot 2 = 1{,}50 = \textbf{1} + 0{,}5$

   • $0{,}5 \cdot 2 = 1{,}00 = \textbf{1} + 0$

   Portanto, $0{,}75 = 0{,}11_2$, e $27{,}75 = 11011{,}11_2$. Para normalizá-lo, nós o reescrevemos como:

2. Os dígitos após o ponto decimal já têm um tamanho adequado. Para float32, estaríamos limitados a 23 bits, mas temos apenas cinco.

A partir da reescrita normalizada, podemos deduzir que:

• $S = 0$, já que o número é positivo;
• $E = \textcolor{blue}{4}+127 = 10000011_2$ (adicionamos $127$ porque $E-127$ deve ser $\textcolor{blue}{4}$); e
• $F = \textcolor{red}{101111}00000000000000000$ (os zeros são preenchidos à direita porque estamos lidando com dígitos fracionários e não com um número inteiro).

Portanto, nossa representação de ponto flutuante é: $0\textcolor{blue}{10000011}\textcolor{red}{101111}00000000000000000$.

Você pode verificar esse resultado com a calculadora de ponto flutuante da Omni!

Os números de ponto flutuante não podem representar todos os números possíveis com precisão total. Isso faz sentido intuitivamente para números suficientemente grandes e para números com um número infinito de casas decimais, como o pi ($\pi$) e o número de Euler ($e$). Mas você sabia que os computadores não conseguem armazenar um valor tão simples como $0{,}1$ com 100% de precisão? Vejamos em detalhes essa afirmação!

Quando você pede a um computador para armazenar $0{,}1$ como um float32, ele armazenará essa cadeia de caracteres binária:

00111101110011001100110011001101

Se você converter isso de volta para decimal com as fórmulas de ponto flutuante que aprendemos acima, obteremos o seguinte:

• $S = 0$
• $E = 01111011_2 = 123$
• $F = 10011001100110011001101_2$

Isso é um pouco mais do que $0{,}1$! O erro (a distância entre o valor de ponto flutuante armazenado e o valor “correto” de $0{,}1$) é $1{,}49 \times 10^{-9}$.

Tentemos corrigir esse erro e fazer a menor alteração possível. Nosso número armazenado é um pouco grande demais, então vamos alterar o último bit de $1$ para $0$ para tornar nosso float um pouco menor. Agora estamos convertendo:

00111101110011001100110011001100

• $S = 0$
• $E = 01111011_2 = 123$
• $F = 10011001100110011001100_2$

E novamente passamos longe de $0{,}1$! Desta vez, o erro é um pouco maior ($5{,}96\times 10^{-9}$). A primeira cadeia de caracteres binária que terminou em 1 estava ainda mais correta do que esta!

Você pode pensar: “e se usássemos mais bits?” Bem, se você fizesse o mesmo com o formato float64, encontraria o mesmo problema, embora menos grave. $0{,}1$ convertido para um ponto flutuante de 64 bits e de volta para decimal é $0{,}100000000000000006$, e o erro aqui é $5{,}55 \times 10^{-18}$. Essa é a maior precisão do float64 em ação, mas o erro ainda não é $0$, a conversão ainda não é sem perdas.

Infelizmente, essa é a desvantagem do onipresente formato de ponto flutuante: não é 100% preciso. Pequenos fragmentos de informação são perdidos e podem causar estragos se não forem levados em conta. Os únicos números que podem ser armazenados perfeitamente como float sem nenhuma perda são potências de 2 escalonadas por inteiros porque é assim que o formato armazena números. Todos os outros números são simplesmente aproximados quando armazenados como um número de ponto flutuante. Ainda assim, isso é o melhor que temos.

O padrão IEEE754 de ponto flutuante permite o armazenamento e processamento eficientes de números em computadores.

• Do ponto de vista do hardware, muitas simplificações das operações de ponto flutuante podem ser feitas para acelerar significativamente a aritmética, graças às especificações do padrão IEEE754.

• Para o software, os pontos flutuantes são muito precisos e normalmente perdem alguns milionésimos (se não menos) por operação, o que permite aplicações científicas e de engenharia de alta precisão.

A representação em ponto flutuante de 12,25 é 01000001010001000000000000000000. Seu sinal é 0, seu expoente é 10000010₂ = 130 e sua fração é 100010...0. Reconstruído em decimal, obtemos:

(-1)⁰ × 2^(130-127) × (1,10001)₂
= 1 × 2³ × 1,53125
= 12,25