Calculadora de Terra Plana versus Redonda

Qual é a melhor maneira de você aprender sobre o mundo? Propor uma teoria e tentar prová-la com observações (ciência)? Ou simplesmente inventar coisas e ignorar fatos óbvios (absurdos)? Aqui na Omni, tendemos a achar que a primeira opção é sempre a melhor. Afinal, foi ela que nos levou à Lua, não foi? Sim, nós realmente estivemos lá!

Para comemorar o Dia Mundial da Ciência pela Paz e Desenvolvimento, celebrado todo dia 10 de novembro, criamos uma calculadora que ajuda você a lutar contra as meias-verdades e as balelas, e a favor da ciência, da observação e da mente aberta.

A calculadora de Terra plana vs. redonda da Omni apresenta experimentos que ajudam a provar que a Terra é de fato redonda. Não se preocupe; você não precisa construir seu próprio foguete para ir ao espaço sideral para verificar. Ainda assim, caso você queira saber qual é o impulso, a variação de momento ou de energia cinética envolvidos em um lançamento de foguete, consulte a calculadora de impulso e momento e a calculadora de energia cinética da Omni.

Temos três experimentos relativamente simples para você reproduzir:

• Pôr do sol duas vezes: ao mudar o ponto de vista acima do solo, você pode ver o pôr do sol duas vezes. Nossa calculadora informa quanto do segundo pôr do sol você verá.
• Objetos que desaparecem: esconda objetos atrás da curvatura da Terra alterando a altura do seu ponto de vista. Essa calculadora mostrará a altura de um objeto que você pode fazer desaparecer.
• Sombra de um bastão: use os comprimentos das sombras projetadas por um bastão em diferentes locais para estimar o comprimento da circunferência da Terra.

Antes de passarmos aos experimentos, vamos dar uma breve visão geral do porquê as pessoas acreditarem em uma Terra plana e no modelo de mundo que elas apresentam.

Surpreendentemente, no país mais rico e tecnologicamente mais desenvolvido do mundo, uma em cada seis pessoas não tem certeza se a Terra é redonda 🤔. É claro que o país é os EUA, e a crença de que Terra é plana pode ser resultado de sua cultura altamente individualista e da desconfiança em relação às autoridades, às instituições e aos especialistas.

Os terraplanistas parecem olhar para o mundo por conta própria, sem referência aos mais de 2.000 anos de descobertas humanas. Eles certamente estão perdendo um bom pedaço da nossa história. Eles também são extremamente desconfiados de qualquer fato que não tenham verificado pessoalmente. Parece que eles têm problemas com confiança.

Eles, então, assumem desafios extraordinários para provar que a Terra é plana, quando há coisas simples que eles poderiam fazer para provar que a Terra é redonda. Aqui estão alguns exemplos:

• "Mad" Mike Hughes construiu seus próprios foguetes movidos a vapor para voar a uma altura de 550 m para fotografar a falta de curvatura do deserto de Mojave. Contudo, você precisa ir a pelo menos 11.000 m para ver a curvatura da Terra. Infelizmente, ele faleceu em fevereiro de 2020 em um voo fracassado de foguete.
• Em 2020, a estrela do YouTube Logan Paul planejava visitar a Antártica para chegar até a borda da Terra plana. No entanto, a viagem não ocorreu, devido à pandemia da COVID-19 e falta de estrutura hospitalar para suportar eventuais problemas.
• O rapper B.o.B. tentou financiar por crowdfunding o lançamento de seu próprio satélite para verificar se a Terra é plana. Ele só conseguiu arrecadar US$ 6.883 de sua meta de US$ 1 milhão. Bem, não importa. Talvez ele possa experimentar nossos experimentos simples e de baixo custo.

Este desenho animado de Tom Fonder resume muito bem os defensores da Terra plana.

No modelo de Terra plana, o mundo é um disco semelhante às engrenagens de uma máquina, com o polo norte no centro. A propósito, se você quiser saber mais como diversas engrenagens podem ser combinadas para mover um sistema mecânico, visite a calculadora de relação de engrenagens da Omni. Ao redor da borda do disco estão o gelo e a neve do "polo sul" Isso forma uma barreira de gelo, que serve para impedir que a água dos oceanos caia do disco para o espaço.

A espessura da crosta terrestre plana não está clara. Entretanto, a massa envolvida deve ser muito menor do que a de uma Terra redonda, de modo que a Terra seria incapaz de manter sua atmosfera. Talvez haja uma cúpula transparente sobre a Terra, impedindo que ela escape.

O modelo tradicional de Terra plana tem o Sol posicionado sobre o disco, circulando no céu como um móbile de bebê e a uma distância muito mais próxima de nós. Isso não explica o pôr e o nascer do Sol. Para que você tenha um pouco de sanidade, vamos imaginar que o disco gira como uma moeda em relação ao Sol. Isso pelo menos nos traria de volta o nascer e o pôr do sol (algo que o animal mais simples poderia observar). Entretanto, não haveria fusos horários, pois o nascer e o pôr do sol seriam no mesmo horário em todo o mundo.

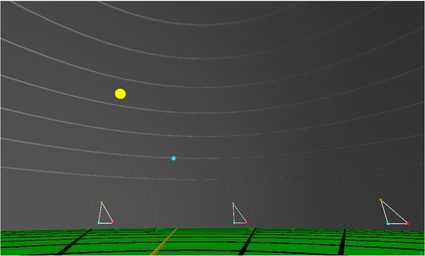
Esse é o principal problema do modelo da Terra plana. Ele está cheio de inconsistências e observações inexplicáveis. Por exemplo, por que é frio tanto no centro quanto na borda do disco?

Vamos voltar a uma forma mais científica de pensar e apresentar o primeiro experimento.

Esse primeiro experimento pode ser muito simples de realizar. Mova-se para cima rápido o suficiente antes que o Sol se esconda no horizonte. Você poderá ver parte do pôr do sol duas vezes! Se você observar isso, então a Terra é de fato redonda. Este experimento calculará quanto de um segundo pôr do sol você poderia ver e quanto tempo você poderia fazer um pôr do sol durar.

O que você veria se a Terra fosse plana? Nenhum segundo pôr do sol 😭. Não importa o quão alto ou rápido você subisse da superfície de uma Terra plana, você não veria o Sol novamente até o amanhecer.

Em uma Terra redonda, quando o Sol se põe, imagine a sombra projetada pelo horizonte da Terra vindo em direção a você e subindo pelo seu corpo. Se você conseguir se antecipar a essa sombra movendo-se para cima com rapidez suficiente, poderá ver o pôr do sol novamente. Vamos dar uma olhada na matemática.

Este artigo nos fornece uma equação que relaciona o tempo com a altura da sombra:

t = 8 ⋅ √h

onde t é o tempo que a sombra leva para subir em altura na quantidade h. Podemos relacionar h com a diferença de altura entre dois pontos de referência e t com o tempo que você leva para subir. Como não podemos nos deslocar instantaneamente da altura mais baixa para a mais alta, precisamos considerar o tempo de deslocamento. Finalmente, para descobrir a quantidade de um segundo pôr do sol que podemos ver novamente, precisamos saber a duração do pôr do sol. Temos, então, essa equação para a porcentagem do segundo pôr do sol que você observará novamente:

Porcentagem do segundo pôr do sol = 100 × (1 - (Duração do pôr do sol - t - Tempo de viagem) / Duração do pôr do sol)

Há algumas maneiras de você ver o Sol novamente logo após ele se pôr, em graus variados. A calculadora de Terra plana vs. redonda da Omni lhe dirá quanto de um segundo pôr do sol você poderá observar. Vamos examinar três opções.

1. Deite-se e fique de pé

Essa ideia é a mais simples em termos de equipamento. Você só precisa de um local onde possa ver o pôr do sol no mar ou em um terreno muito plano (como um deserto). Um belo céu sem nuvens também ajudará. Tudo o que você precisa fazer é assistir ao pôr do sol enquanto está deitado. Quando não conseguir mais ver o Sol, levante-se imediatamente o mais rápido que puder. Você deverá conseguir ver uma pequena parte do topo do Sol novamente.

Aqui está como você pode usar a calculadora para calcular exatamente o quanto.

1. Selecione um local mais próximo de você ou insira manualmente a duração do pôr do sol onde você está.
2. Insira a altura inicial mais baixa do nível dos seus olhos. Nesse caso, quando você estiver deitado. Recomendamos que você insira cerca de 20 cm.
3. Informe quanto tempo você levará para chegar à altura mais alta. Calculamos que seja cerca de meio segundo, mas você pode cronometrar o tempo para verificar.
4. Insira a altura final do nível dos seus olhos quando você estiver em pé. Você pode medir isso subtraindo a distância do topo da cabeça até a altura dos seus olhos.
5. Você obterá então a porcentagem do Sol que poderá ver novamente. Você quer ver mais? Tente alterar os valores na calculadora ou vá para as variações mais avançadas do experimento abaixo.

Você deve ser capaz de ver cerca de 5% do segundo pôr do sol com esse método.

2. Elevação rápida em um arranha-céu

Para ver mais do segundo pôr do sol, você terá que ir mais alto e mais rápido para ficar à frente da sombra do horizonte. Um arranha-céu com um elevador rápido é uma opção. Esse fenômeno foi observado no hotel Burj Khalifa em Dubai.

Para selecionar os valores de entrada para esse arranha-céu, escolha "Elevador de arranha-céus - Burj Khalifa hotel" na lista suspensa. Se você quiser tentar isso em outro edifício, ajuste os dados de entrada na calculadora.

Você deve conseguir ver cerca de 88% do pôr do sol novamente e, assim, quase dobrar a duração. Se você é um amante do pôr do sol, este deve ser o seu experimento.

3. Drone com uma câmera

Outra ideia é usar um drone de boa qualidade que tenha um recurso de câmera de transmissão ao vivo. Encontramos um drone que pode atingir 1.000 m em 200 segundos. Se você selecionar "Drone" na lista suspensa, verá que é possível observar cerca de um terço do pôr do sol novamente com esse método.

Verifique a velocidade e a altura que seu drone pode atingir e ajuste os valores na calculadora.

Neste experimento, esconderemos parte de um objeto atrás da curvatura da Terra. Você precisará estar próximo de um rio ou de uma praia, onde a margem mais distante esteja a pelo menos 2 km de distância, e o dia precisa estar calmo e sem vento.

Além disso, para evitar o efeito miragem (ou refração da luz), faça o experimento pela manhã, quando estiver frio. É também por isso que não recomendamos que este experimento seja realizado em um deserto, já que o efeito de miragem significa que você não conseguirá ver os objetos na margem distante com clareza suficiente.

Neste vídeo do YouTube, uma pessoa fez com que um caminhão a 7 km de distância desaparecesse na margem oposta de um lago, abaixando a câmera para mais perto do chão.

Como alternativa, um parque eólico visto do mar também é uma boa opção, como demonstra esta fotografia:

Observe que quanto mais longe você estiver de um moinho de vento, mais ele ficará oculto. É disso que trata este experimento: calcular quanto de um objeto distante você pode esconder por trás da curvatura da Terra.

Neste experimento, começaremos em um ponto de referência alto e depois desceremos para um ponto de referência baixo para ocultar um objeto distante. Em termos matemáticos, descobriremos o quanto ele está oculto nos pontos de referência alto e baixo e calcularemos a diferença.

Para calcular a altura obscurecida, primeiro precisamos saber a distância até o horizonte. Isso é dado por esta equação:

a = √[(r + h)² - r²]

onde:

• a – É a distância até o horizonte;
• h – É o nível do ponto de vista acima do solo; e
• r – É o raio da Terra, igual a 6.371 km.

Em seguida, inserimos o resultado em uma segunda equação que calcula quanto do objeto é obscurecido, x, se visto de uma altura zero:

x = √(a² - 2ad + d² + r²) - r

A diferença entre os dois valores de x é a altura do objeto que podemos fazer desaparecer mudando nosso ponto de referência.

OK, então você encontrou um local excelente, como uma praia com a margem a alguns quilômetros de distância. Para ver qualquer objeto na margem distante, você precisará de bons binóculos. Melhor ainda, uma câmera de vídeo com uma lente de zoom potente. Isso também permitiria que você gravasse o experimento, como no vídeo acima.

Para obter uma visão estável por meio dos binóculos ou da câmera, é recomendável montá-los em um tripé. O uso de um tripé também permite que você meça as duas alturas com precisão.

Veja aqui como usar a calculadora para descobrir o tamanho do objeto que você pode conseguir fazer desaparecer por trás da curvatura da Terra.

1. Meça a distância até a margem mais distante da praia. Você pode usar um mapa de papel ou o recurso de medição do Google Maps para fazer isso. Insira a distância no campo correspondente na calculadora (Distância até o objeto).
2. Meça a altura acima do solo do nível dos seus olhos quando estiver em pé ou da sua câmera quando ela estiver na posição mais alta. Insira essa altura no próximo campo de entrada.
3. Faça o mesmo quando você estiver deitado ou quando a câmera estiver na posição mais baixa. Para maximizar o efeito, tente ficar o mais baixo possível do nível da água.
4. Você verá que a altura de um objeto obscurecido pela curvatura da Terra é calculada para você. Se você achar que o objeto é pequeno demais para ser visto, tente aumentar a diferença de altura.

Se a Terra for plana, você não verá nenhuma diferença nos objetos do lado oposto da praia, independentemente da altura do chão em que você os veja.

Esse experimento não apenas prova que a Terra é redonda, mas você também pode estimar o comprimento da circunferência da Terra. Foi exatamente isso que o matemático grego Eratóstenes fez em Alexandria, por volta de 240 a.C.. Ele sabia que em Assuã, a cerca de 800 km ao sul, havia um poço onde a luz do sol chegava ao fundo ao meio-dia no solstício de verão. Ao mesmo tempo, ele mediu a sombra projetada por um bastão em Alexandria.

Partindo do princípio de que a Terra é redonda e o Sol está distante, e usando a matemática que veremos a seguir, ele concluiu que o comprimento da circunferência da Terra era cerca de 50 vezes a distância entre Alexandria e Assuã. Isso está dentro de 10% da resposta correta. Um resultado fantástico para um experimento tão simples realizado há mais de 2.000 anos.

Observando o triângulo formado pelo bastão e a sombra, podemos aplicar a função trigonométrica arco tangente para calcular o ângulo entre o bastão e o raio de luz solar, usando a equação:

θ = arctan(Comprimento da sombra / Altura do bastão)

Então, fazemos essa medida nos dois locais. Como esses dois ângulos se relacionam com o comprimento da circunferência da Terra? A figura abaixo nos ajudará a responder a essa pergunta.

Usando um pouco de geometria, podemos mostrar que o ângulo α entre as linhas que passam pelos locais A e B e o centro da Terra é a diferença entre os ângulos das sombras dos bastões:

α = θ₂ - θ₁

Agora sabemos o comprimento do arco (distância ao longo da superfície da Terra) entre A e B e o ângulo α. Isso nos permite simplesmente aumentar a distância para calcular o comprimento (perímetro) da circunferência total da Terra, usando a equação:

Perímetro da Terra = Distância A → B × (360° / α)

É importante observar que a distância de A até B deve ser considerada como aquela medida se você pudesse viajar apenas para o norte ou para o sul (a distância norte-sul). Precisamos dessa distância, pois somente quando você viaja para o norte é que a sombra projetada pelo bastão fica mais longa.

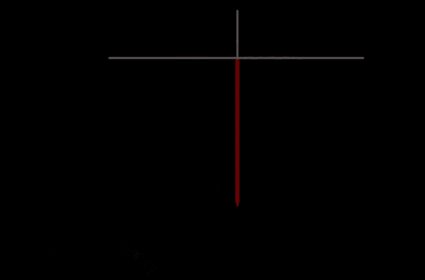
Supondo que o ponto A esteja ao sul do ponto B, em um mapa, desenhe uma linha para o norte a partir do ponto A. Em seguida, desenhe uma linha para o leste a partir do ponto B. A distância norte-sul é o comprimento do ponto A até o ponto em que as duas linhas que você desenhou se cruzam.

Há duas maneiras de você fazer esse experimento. Você pode viajar uma distância considerável para o norte ou para o sul (mais de 160 quilômetros, mas quanto mais longe, melhor) ou combinar com um amigo que more longe para ajudá-lo.

Vamos começar com a opção de viajar. É melhor você tentar fazer isso no dia mais curto ou mais longo do ano, pois a duração do dia é relativamente estável. Isso reduzirá os erros no ângulo da sombra medido nos dois locais. Aqui estão as instruções passo a passo:

1. Meça o comprimento do seu bastão. Você precisará inserir essa medida no primeiro campo de entrada da calculadora. Se parte do bastão estiver no solo, inclua apenas o comprimento acima do solo.
2. Meça o comprimento da sombra no local A, no horário local do meio-dia. Se não for um dia ensolarado, espere até que você tenha um. Insira o comprimento da sombra na calculadora, e o ângulo da sombra será calculado para você.
3. Vá até o local B e faça o mesmo procedimento da etapa 2.
4. Usando um mapa, meça a distância norte-sul entre os dois locais e insira esse valor na calculadora (consulte as instruções acima).
5. Você receberá uma resposta para sua estimativa do comprimento da circunferência da Terra e o quão próximo você chegou da resposta real.

Se você tiver um amigo em outro local para ajudá-lo, melhor ainda! O experimento será mais preciso se você fizer as duas medições no mesmo dia do ano e no mesmo horário solar. Nesse caso, as etapas são basicamente as mesmas. Certifique-se de que as duas varas tenham o mesmo comprimento e que você meça a sombra ao meio-dia, horário local, no mesmo dia. Essa opção é muito mais fácil e pode ser realizada em qualquer dia ensolarado do ano.

Por exemplo, vamos viajar de um ponto A até B, cuja distância norte-sul seja de cerca de 1.609 km. O bastão tem 0,91 m de comprimento e medimos um comprimento de sombra de 0,91 m em A. Isso significa um ângulo de sombra de 45°. Em seguida, viajamos para B e medimos uma sombra de 1,59 m, o que significa que o ângulo da sombra neste ponto é de cerca de 60°.

Insira todos esses números na calculadora e obteremos um resultado de 38.577 km. Isso está dentro de 4% do comprimento real medido entre os polos de 40.008 km.

Vamos imaginar que os defensores da Terra plana estejam certos por um momento. Como o exemplo acima funcionaria em um modelo de Terra plana?

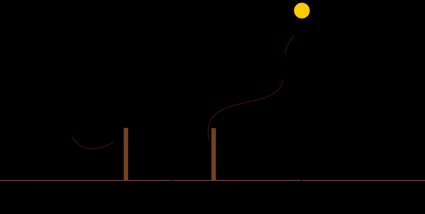
Em um modelo de Terra plana, os bastões ainda projetarão sombras de diferentes comprimentos. No entanto, o resultado da aplicação de trigonometria leva a um resultado estranho. Considerando o diagrama acima e aplicando nossos conhecimentos de trigonometria, podemos dizer que:

d = h ⋅ |tan θ₂ - tan θ₁|

Usando os ângulos de 45° e 60° e 1.609 km para d, vemos que a distância até o Sol h é

h = 1.609 / (1,73 - 1) = 2.204 km

Isso parece muito próximo. Entretanto, o modelo da Terra plana pode dizer que o Sol é muito menor do que a ciência concluiu.

Agora podemos calcular as duas outras distâncias até o Sol a partir dos dois locais:

R₁ = h / cos θ₁ = 2.204 / cos(45°) = 3.117 km

R₂ = h / cos θ₂ = 2.204 / cos(60°) = 4.408 km

Esse resultado significa que, ao viajar 1.609 km para o sul, o Sol deveria ter ficado menor em cerca de 40%. Na realidade, como você pode verificar por si só, o Sol não parece ficar menor à medida que você viaja para o sul.

Portanto, podemos concluir que o modelo da Terra plana está errado. Ele não está de acordo com a observação. Essa é a propriedade fundamental de qualquer modelo científico. Ele deve estar de acordo com os resultados experimentais.

A noção de que a Terra é redonda (ou mais precisamente esférica) é bastante antiga! Na Grécia Antiga, cientistas e filósofos estavam cientes desse fato já no século V a.C.

Mesmo nos séculos posteriores, o modelo esférico foi mais amplamente aceito e apenas marginalmente questionado fora das bases puramente mitológicas: o aparente ressurgimento e a relevância dessa teoria nos tempos modernos são uma consequência da mudança em nossos métodos de comunicação.

Para calcular o comprimento da circunferência da Terra usando sombras:

1. Peça a um amigo, que viva em uma latitude diferente, para executar as mesmas etapas que você; em seguida:
2. Coloque verticalmente um bastão de comprimento conhecido no chão.
3. Meça o ângulo entre o bastão e os raios solares em um determinado horário do dia local.
4. Use a fórmula:
   θ = arctan(Comprimento da sombra / Altura do bastão).
5. Agora, use esta fórmula para o comprimento da circunferência da Terra:
   Perímetro da Terra = Distância × (360° / α),
   onde:
   • Distância é a distância norte-sul entre os bastões; e
   • α é a diferença entre os ângulos calculados anteriormente.

Para ver a curvatura da Terra, você deve estar a uma altitude de cerca de 10,5 km. Essa é aproximadamente a altitude de voo de um avião de passageiros. No entanto, para ver a curvatura corretamente, você precisa de um horizonte completamente limpo (sem nuvens) e um campo de visão de pelo menos 60 graus. Essas duas condições raramente são satisfeitas a partir das janelas do seu avião, mas você pode tentar.

Além disso, observe que a curvatura não é visível nem mesmo do cume do Monte Everest!

Para provar que a Terra é redonda, vá à praia! Se houver um trecho de mar longo o suficiente à sua frente, você pode simplesmente esperar que um navio se aproxime da costa. Você verá primeiro a parte superior do navio aparecendo acima do horizonte, seguida lentamente pelo resto do navio.
Como a Terra é redonda, sua curvatura cobre parte do navio. A parte coberta fica menor à medida que o navio se aproxima de você.

Agora, a parte difícil é convencer os céticos de que essa é uma resposta definitiva!