Omni Calculator logo
Última atualização:

Calculadora de Módulo de Resistência

Novo

Índice

Como calcular o módulo de resistência a partir do momento de inérciaMódulo de resistência plástico: além do módulo de resistência elásticoFórmulas de módulo de resistência para uma seção retangular e outras formasQuais são as unidades do momento de inércia de área?Perguntas frequentes

Esta ferramenta Omni calcula o módulo de resistência, uma das propriedades geométricas mais críticas no projeto de vigas sujeitas à flexão. Além disso, ela determina o eixo neutro e o momento de inércia de área dos perfis estruturais mais comuns (se você procura pela definição do momento de inércia de área, consulte nossa calculadora de momento de inércia).

As fórmulas para o módulo de resistência de um retângulo ou círculo são relativamente fáceis de calcular. Ainda assim, quando você lida com geometrias complexas como um T, um canal ou uma viga I, nossa calculadora pode economizar tempo e nos ajudar a evitar erros.

Nas seções a seguir, discutiremos os dois tipos de módulo de resistência, como calcular o módulo de resistência a partir do momento de inércia e apresentaremos as fórmulas de módulo de resistência de um retângulo e de muitas outras formas comuns.

Como calcular o módulo de resistência a partir do momento de inércia

O módulo de resistência é usado pelos engenheiros para prever rapidamente a tensão máxima que um momento de flexão causará em uma viga. A equação para o valor absoluto máximo da tensão em uma viga sujeita a flexão é dada por:

σm=McI\sigma_m = \frac{Mc}{I}

onde:

  • σm\sigma_m: valor absoluto máximo da tensão em uma seção específica da viga;
  • MM: momento de flexão ao qual a viga está sujeita nessa seção;
  • cc: maior distância do eixo neutro até a superfície do perfil; e
  • II: momento de inércia de área sobre o eixo neutro da seção (também calculado por esta ferramenta).

Vamos lembrar que, em um círculo, a maior distância é igual ao raio, enquanto em um retângulo é igual à metade da altura.

Como a relação I/cI/c depende apenas das características geométricas, podemos definir uma nova propriedade geométrica a partir dela, chamada de módulo de resistência, denotada pela letra SS:

S=IcS = \frac{I}{c}

Assim como o momento de inércia de área, essa nova propriedade geométrica está disponível em muitas tabelas e calculadoras, mas se você quiser saber como calcular o módulo de resistência a partir do momento de inércia, basta dividir II por cc, e você o obterá.

Finalmente, podemos relacionar o módulo de resistência à tensão e ao momento:

σm=MS\sigma_m = \frac{M}{S}

🙋 Essa equação parece familiar para você? Ela é equivalente à equação da tensão axial: σ=FA\sigma = \frac{F}{A}, onde vemos que o momento de flexão é análogo à força axial, enquanto o módulo de resistência é análogo à área da seção transversal. Você pode usar nossa calculadora de tensão mecânica para determinar a tensão axial.

Considere os seguintes pontos ao calcular o módulo de resistência e as tensões máximas:

  • Determinamos o valor do momento de flexão por meio de uma análise estática ou estrutural da viga.
  • Para obter o módulo da resistência, podemos usar tabelas para perfis estruturais predefinidos, mas essa calculadora é a melhor opção se você estiver lidando com geometrias personalizadas.
  • Se estivermos considerando uma viga de seção uniforme (caso usual), a tensão máxima e o momento de flexão máximo estarão localizados no mesmo ponto. Se esse não for o caso, σm\sigma_m poderá estar localizado em um ponto diferente.
  • As fórmulas anteriores se aplicam a materiais que exibem um comportamento elástico e obedecem à lei de Hook. Quando há deformação plástica em vez de deformação elástica, precisamos usar o módulo de resistência plástico.

Módulo de resistência plástico: além do módulo de resistência elástico

As equações anteriores não se aplicam quando submetemos um material de viga a tensões além da resistência ao escoamento, pois elas pressupõem que a tensão e a deformação estão linearmente relacionadas. Nesse caso, devemos usar o módulo de resistência plástico. Semelhante ao módulo de resistência elástico SS, sua contraparte plástica fornece uma relação entre tensão e momento:

Mp=ZσYM_p = Z\sigma_Y

onde:

  • MpM_p: momento plástico da seção;
  • ZZ: módulo de resistência plástico; e
  • σY\sigma_Y: resistência ao escoamento do material da barra.

O momento plástico refere-se ao momento exigido para causar deformação plástica em toda a área transversal de uma seção do perfil.

A utilidade da última equação é que podemos prever o momento de flexão que causará a deformação plástica conhecendo apenas a resistência ao escoamento e o módulo de resistência plástico.

O gráfico a seguir descreve melhor o conceito de momentos plásticos:

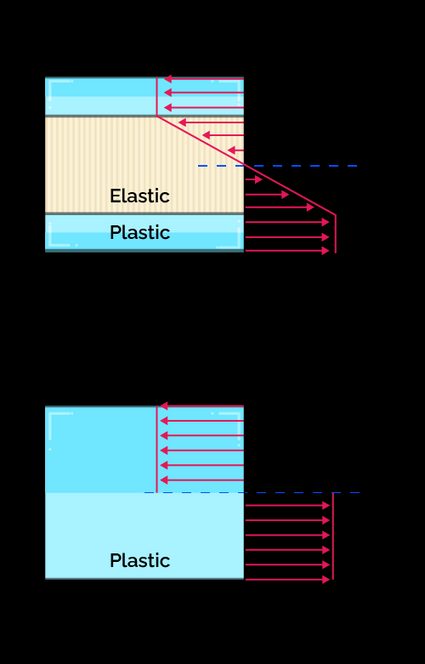
Imagem da distribuição de tensão durante a deformação plástica
Representação gráfica da distribuição da tensão de flexão durante as deformações plásticas. Estamos assumindo um modelo de plasticidade ideal, portanto, as distribuições reais de tensão não são tão uniformes.

Para que ocorra a deformação plástica, devemos causar alguma tensão igual à força de escoamento do material. Como você pode notar, a transição de elástico para plástico não é uniforme em todo o perfil, pois algumas regiões possuirão resistência ao escoamento antes de outras.

Quando toda a seção atinge a tensão de escoamento, ocorre a deformação plástica da seção. O momento de flexão necessário para deformar totalmente a seção é chamado de momento plástico.

Fórmulas de módulo de resistência para uma seção retangular e outras formas

Na tabela a seguir, listamos a fórmula do módulo de resistência para uma seção retangular e muitos outros perfis (role a tabela para os lados para ver todas as equações):

Forma

Módulo de Resistência Elástico

Quadrado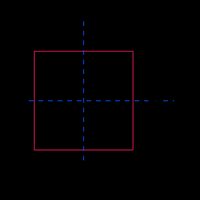

Image of a square section and its dimensions

yc=xc=a/2y_c = x_c = a/2

Ix=Iy=a412I_x = I_y = \frac{a^4}{12}

Sx=Sy=Ixyc=a36S_x = S_y =\frac{I_x}{y_c} = \frac{a^3}{6}

Retângulo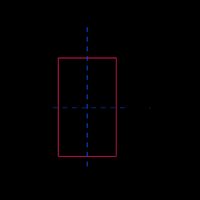

Image of a rectangular section and its dimensions

yc=d/2y_c=d/2

xc=b/2x_c=b/2

Ix=bd312I_x = \frac{bd^3}{12}

Iy=db312I_y = \frac{db^3}{12}

Sx=Ixyc=bd26S_x = \frac{I_x}{y_c} = \frac{b d^2}{6}

Sy=Iyxc=db26S_y = \frac{I_y}{x_c} = \frac{d b^2}{6}

Tubo Retangular

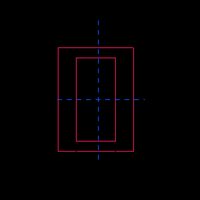Image of a hollow rectangle section and its dimensions

yc=d/2y_c=d/2

xc=b/2x_c=b/2

Ix=bd3−bidi312I_x = \frac{bd^3-b_id_i^3}{12}

Iy=db3−dibi312I_y = \frac{db^3-d_ib_i^3}{12}

Sx=IxycS_x = \frac{I_x}{y_c}

Sy=IyxcS_y = \frac{I_y}{x_c}

Seção em T

Image of a hollow tee section and its dimensions

yc=bt2+twd(2t+d)2(tb+twd)y_c=\frac{bt^2+t_wd(2t+d)}{2(tb+t_wd)}

xc=b/2x_c=b/2

A=tb+twdA = tb + t_wd

Ix=b(d+t)3−d3(b−tw)3          −A(d+t−yc)2I_x = \frac{b(d+t)^3-d^3(b-t_w)}{3} \\\ \ \ \ \ \ \ \ \ \ - \footnotesize A(d+t-y_c)^2

Iy=tb3+dtw312I_y = \frac{tb^3+dt_w^3}{12}

Sx=Ixd+t−ycS_x = \frac{I_x}{d+t-y_c}

Sy=IyxcS_y = \frac{I_y}{x_c}

Seção em C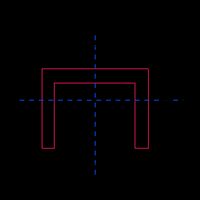

Image of a hollow rectangle section and its dimensions

yc=bt2+2twd(2t+d)2(tb+2twd)y_c=\frac{bt^2+2t_wd(2t+d)}{2(tb+2t_wd)}

xc=b/2x_c=b/2

Ix=b(d+t)3−d3(b−2tw)3          −A(d+t−yc)2I_x = \frac{b(d+t)^3-d^3(b-2t_w)}{3} \\\ \ \ \ \ \ \ \ \ \ -\footnotesize A(d+t-y_c)^2

Iy=(d+t)b3−d(b−2tw)312I_y = \frac{(d+t)b^3-d(b-2t_w)^3}{12}

Sx=Ixd+t−ycS_x = \frac{I_x}{d+t-y_c}

Sy=IyxcS_y = \frac{I_y}{x_c}

A=tb+2twdA = tb + 2t_wd

Viga de Flange Larga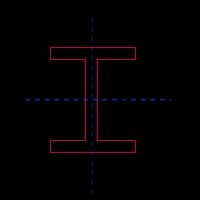

Image of a hollow rectangle section and its dimensions

yc=d/2+ty_c=d/2+t

xc=b/2x_c=b/2

Ix=b(d+2t)3−(b−tw)d312I_x = \frac{b(d+2t)^3-(b-t_w)d^3}{12}

Iy=b3t6+tw3d12I_y = \frac{b^3t}{6} + \frac{t_w^3d}{12}

Sx=IxycS_x = \frac{I_x}{y_c}

Sy=IyxcS_y = \frac{I_y}{x_c}

Ângulo

Image of a hollow rectangle section and its dimensions

yc=d2+bt+−t22(b+d−t)y_c=\frac{d^2+bt+-t^2}{2(b+d-t)}

xc=b2+dt−t22(b+d−t)x_c=\frac{b^2+dt-t^2}{2(b+d-t)}

A=t(b+d−t)A = t(b+d-t)

Ix=bd3−(b−t)(d−t)33          −A(d−yc)2\footnotesize I_x = \frac{bd^3-(b-t)(d-t)^3}{3} \\\ \ \ \ \ \ \ \ \ \ -A(d-y_c)^2

Iy=db3−(d−t)(b−t)33          −A(b−xc)2\footnotesize I_y = \frac{db^3-(d-t)(b-t)^3}{3} \\\ \ \ \ \ \ \ \ \ \ -A(b-x_c)^2

Sx=Ixd−ycS_x = \frac{I_x}{d-y_c}

Sy=Iyb−xcS_y = \frac{I_y}{b-x_c}

A=t(b+d−t)A = t(b+d-t)

Círculo

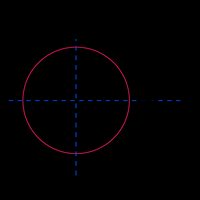Image of a circular section and its dimensions

yc=xc=Ry_c = x_c = R

Ix=Iy=π4R4I_x = I_y = \frac{\pi}{4}R^4

Sx=Sy=Ixyc=π4R3S_x = S_y =\frac{I_x}{y_c} = \frac{\pi}{4}R^3

Tubo Circular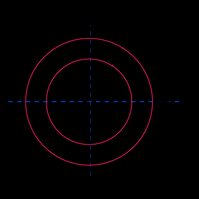

Image of a hollow circular section and its dimensions

yc=xc=Ry_c = x_c = R

Ix=Iy=π4(R4−Ri4)I_x = I_y = \frac{\pi}{4}(R^4-R_i^4)

Sx=Sy=IxycS_x = S_y =\frac{I_x}{y_c}

🔎 Você tem interesse em calcular deflexões em vez de tensões? Não deixe de acessar a calculadora de deflexão de vigas da Omni.

Quais são as unidades do momento de inércia de área?

As unidades do momento de inércia de área são mm⁴ ou m⁴ no Sistema Internacional de Unidades e in⁴ nas unidades habituais dos Estados Unidos. Por outro lado, as unidades do módulo de resistência elástico são mm³, m³ e in³.

Perguntas frequentes

Como calcular o módulo de resistência de um tubo circular?

Para calcular o módulo de seção de um tubo circular de espessura t e raio R, use a fórmula do módulo de seção para um anel muito fino: S = πR²t, ou siga os passos a seguir:

  1. Meça o raio R e a espessura t do tubo circular.
  2. Multiplique o número π pelo quadrado do raio.
  3. Multiplique o último resultado pela espessura.
  4. É isso! Você também pode usar nossa calculadora de módulo de resistência e obter a resposta instantaneamente.

Quais são as unidades do módulo de resistência elástico?

As unidades do módulo de resistência elástico são mm³ ou m³ no Sistema Internacional de Unidades e in³ nas unidades habituais dos Estados Unidos. Curiosamente, essas são as mesmas unidades de volume.

Quais são as dimensões de um perfil W6 x 12?

As dimensões de um perfil W6 x 12 são:

  • Área: 22,90 cm² ou 3,55 in²;
  • Profundidade: 15,32 cm ou 6,03 in;
  • Largura da flange: 10,16 cm ou 4,00 in;
  • Espessura da flange: 7,11 mm ou 0,280 in.; e
  • Espessura da alma: 5,84 mm ou 0,230 in.

Além disso, seu momento de inércia de área em relação ao eixo centroidal horizontal é de 919,9 cm⁴ (22,1 in⁴), enquanto o módulo de seção elástica em relação ao mesmo eixo é de 120 cm³ (7,31 in³).

Qual o módulo de resistência para uma seção retangular?

A fórmula do módulo de seção elástica de um retângulo é S = bd²/6, em que:

  • S: módulo de resistência;
  • d: altura do retângulo; e
  • b: base ou largura do retângulo.

Leve em conta que esse módulo de resistência é calculado sobre o eixo centroidal horizontal.

Podemos derivar a fórmula do módulo de resistência para uma seção retangular dividindo seu momento de inércia de área (bh³/12) pela distância máxima até o eixo neutro (h/2):

S = (bh³/12)/(h/2) = bh²/6

Qual é o módulo de resistência para uma seção quadrada?

A fórmula do módulo de resistência elástico de um quadrado é S = a³/6, onde:

  • S: módulo de resistência; e
  • a: comprimento de qualquer um dos lados do quadrado;

Podemos derivar a fórmula do módulo de resistência para uma seção quadrada dividindo seu momento de inércia de área (a⁴/12) pela distância máxima até o eixo neutro (a/2):

S = (a⁴/12)/(a/2) = a³/6

Como calcular o módulo de resistência plástico de uma seção em I?

Para calcular o módulo de resistência plástico de uma seção em I, use as fórmulas:

  • Zₓ = 0,25d²tᵥᵥ + bt(d + t)
  • Zᵧ = 0,5b²t + 0,25dtᵥᵥ²

onde:

  • Zₓ: módulo de resistência plástico em relação ao eixo neutro plástico horizontal;
  • Zᵧ: módulo de resistência plástico em relação ao eixo neutro plástico vertical;
  • d: comprimento da trama;
  • tᵥᵥ: espessura da alma;
  • t: espessura do flange; e
  • b: comprimento do flange.

Entradas

Imagem de uma seção retangular.

© Omni Calculator

Na seção "Fórmulas do módulo de resistência da seção" do artigo, apresentamos as fórmulas com as quais o módulo de resistência da seção é calculado. Se você acha que estamos nos esquecendo de uma forma importante, informe-nos.

Check out 39 similar materials and continuum mechanics calculators 🧱
Angle of reposeAngle of twistBend allowance...36 more