Kalkulator kombinacji

Nasz kalkulator kombinacji (kalkulator n po r) to narzędzie, które pomaga nie tylko określić liczbę kombinacji w zbiorze (często oznaczanych jako nCr), ale także pokazuje każdą możliwą kombinację (lub permutację) twojego zbioru, aż do 20 elementów w zbiorze. Bądź jednak ostrożny! Wykonanie tak dużych obliczeń może zająć naszemu generatorowi kombinacji nawet kilka sekund. Jeśli zastanawiasz się, ile różnych kombinacji można stworzyć z r elementów pochodzących z określonej liczby n elementów, już teraz wypróbuj nasz kalkulator kombinacji!

Jeśli nadal nie jesteś pewien, czym jest kombinacja, to wszystko wyjaśniamy w poniższym artykule. Znajdziesz tu definicję kombinacji wraz ze wzorem na liczbę kombinacji (z powtórzeniami i bez powtórzeń). Pokażemy ci również, jak obliczać kombinacje oraz czym jest kombinacja liniowa i prawdopodobieństwo kombinacji. Na koniec powiemy o związku pomiędzy permutacją a kombinacją. Krótko mówiąc, permutacja bierze pod uwagę kolejność elementów w przeciwieństwie do kombinacji. Więcej informacji znajdziesz poniżej!

Czy zastanawiałeś się kiedyś, jakie są twoje szanse na wygranie głównej nagrody w loterii? Jak prawdopodobna jest wygrana nagrody za drugie miejsce? Aby odpowiedzieć na te oraz inne podobne pytania, musisz użyć kombinacji. Mamy specjalne narzędzie dedykowane do tego typu problemów. Nasz kalkulator loterii 🇺🇸 nie tylko szacuje prawdopodobieństwo kombinacyjne wygranej w dowolnej grze loteryjnej, ale także podaje wzór na szanse wygranej w loterii. Wypróbuj go, a dowiesz się jak duże (lub małe) są te wartości w rzeczywistości!

Definicja kombinacji mówi, że jest to liczba sposobów, na jakie można wybrać r elementów ze zbioru zawierającego n różnych obiektów (dlatego takie problemy często nazywane są problemami „n po r”). Kolejność, w jakiej wybieramy elementy, nie jest istotna w przeciwieństwie do permutacji (obszerne wyjaśnienie tego problemu znajdziesz w części permutacja i kombinacja).

Poszukiwania wszystkich kombinacji zbioru obiektów jest problemem czysto matematycznym. Prawdopodobnie wiesz już na przykład, jak znaleźć największy wspólny dzielnik (NWD) lub jak znaleźć najmniejszą wspólną wielokrotność (NWW). Cóż, kombinacja to zupełnie inna historia. Zobaczmy, jak skomplikowane może być to zadanie.

Wyobraź sobie worek wypełniony dwunastoma kulami, gdzie każda z nich jest innego koloru. Wybierasz losowo pięć kul. Ile różnych zestawów kul możesz otrzymać? Albo, innymi słowy, ile różnych kombinacji możesz uzyskać?

Matematycy podają dokładne rozwiązanie wielu różnych problemów, np. jak obliczyć powierzchnię kwadratu lub jak obliczyć objętość obiektu. Czy istnieje podobne podejście do oszacowania liczby kombinacji w powyższym przykładzie z kulkami?

Na szczęście nie trzeba wypisywać wszystkich możliwych zestawów! Jak w takim razie obliczyć kombinacje? Możesz skorzystać z poniższego wzoru, który pozwoli ci błyskawicznie określić liczbę kombinacji:

gdzie:

• $C(n,r)$ — liczba kombinacji,
• $n$ — całkowita liczba elementów w zbiorze, oraz
• $r$ — liczba wybranych elementów tego zbioru.

Wykrzyknik $!$ oznacza silnię. Sprawdź nasz kalkulator silni 🇺🇸, aby uzyskać więcej informacji na ten temat. Wyrażenie po prawej stronie jest również znane jako symbol Newtona.

Zastosujmy powyższy wzór do naszego problemu z kolorowymi kulkami. Musimy określić, ile jest różnych kombinacji:

Wynik możesz sprawdzić za pomocą naszego kalkulatora nCr. Wygeneruje on również wszystkie możliwe kombinacje! Pamiętaj jednak, że aż 792 różnych kombinacji to już całkiem sporo do pokazania. Aby uniknąć sytuacji, w której jest zbyt wiele kombinacji do wyświetlenia, ograniczyliśmy generator kombinacji do określonej, maksymalnej liczby kombinacji (domyślnie 2000). Możesz to zmienić w trybie zaawansowanym (Advanced mode), kiedy tylko chcesz.

Można zauważyć, że zgodnie ze wzorem na liczbę kombinacji, możliwości wyboru tylko jednego elementu wynoszą po prostu $n$. Z drugiej strony, jeśli musisz wybrać wszystkie elementy, istnieje tylko jeden sposób, aby to zrobić. Sprawdźmy tę własność kombinacji na naszym przykładzie. Masz całkowitą liczbę obiektów, która jest równa $n = 12$. Każda litera wyświetlana w kalkulatorze nCr reprezentuje odrębny kolor kuli, np. A to kolor czerwony, B — żółty, C — zielony itd. Jeśli z tego zbioru wybierzesz tylko jeden element $r = 1$ na raz, to liczba kombinacji wyniesie $12$ — bo jest 12 różnych kul. Jeśli jednak wybierzesz $r = 12$ elementów, to będzie tylko $1$ możliwa kombinacja, która zawiera każdą kulę. Spróbuj tego sam z kalkulatorem n po r!

Do tego momentu prawdopodobnie wiesz już wszystko, co najważniejsze o kombinacjach i wzorze na liczbę kombinacji. Jeśli nadal nie masz dość, w kolejnych etapach piszemy więcej o różnicach między permutacją a kombinacją (które często błędnie są uważane za to samo), prawdopodobieństwie kombinacji oraz kombinacji liniowej.

Wyobraź sobie, że masz taki sam worek wypełniony kolorowymi kulami jak w przykładzie z poprzedniego rozdziału. Ponownie wybierasz losowo pięć kul, ale tym razem kolejność jest ważna — ma znaczenie, czy wybierzesz czerwoną kulę jako pierwszą, czy jako trzecią. Weźmy prostszy przykład, w którym wybierasz trzy kulki oznaczone R (czerwona), B (niebieska), G (zielona). Istnieje sześć permutacji tego zestawu (kolejność liter określa kolejność wyciąganych kul): RBG, RGB, BRG, BGR, GRB, GBR, a definicja kombinacji mówi, że istnieje tylko jedna kombinacja! To jest właśnie ta zasadnicza różnica.

Z definicji permutacja jest aktem ustawienia wszystkich elementów zbioru w pewien ciąg lub kolejność. W praktyce, często uogólniamy to pojęcie i rezygnujemy z wymogu użycia wszystkich elementów danego zbioru. To właśnie czyni permutację i kombinację tak podobnymi. W tym znaczeniu permutacja określa liczbę sposobów, na jakie można wybrać i ułożyć r elementów ze zbioru zawierającego n różnych obiektów. Nazywa się to r-wyrazową permutacją zbioru n (albo inaczej wariacjami). Jeśli chcesz uzyskać jeszcze bardziej szczegółowe wyjaśnienie, kalkulator permutacji 🇺🇸 powinien pomóc ci w tej sprawie.

Poniżej znajdziesz wzór na permutację:

Czy to równanie nie wygląda podobnie do wzoru na liczbę kombinacji? W rzeczywistości, jeśli znasz liczbę kombinacji, możesz też łatwo obliczyć liczbę permutacji:

Jeśli w kalkulatorze kombinacji włączysz zaawansowany tryb (Advanced mode), będziesz mógł znaleźć liczbę permutacji.

Możesz się zastanawiać kiedy powinieneś użyć permutacji zamiast kombinacji. Cóż, to zależy od tego, czy musisz wziąć pod uwagę kolejność, czy nie. Na przykład, powiedzmy, że masz talię dziewięciu kart z cyframi od 1 do 9. Wyciągasz trzy losowe karty i układasz je na stole, tworząc trzycyfrową liczbę, np. 425 lub 837. Ile różnych liczb możesz utworzyć?

Sprawdź wynik za pomocą naszego kalkulatora nCr! A ile jest różnych kombinacji?

Liczba kombinacji jest zawsze mniejsza od liczby permutacji. Tym razem jest sześciokrotnie mniejsza (jeśli pomnożymy 84 przez $3! = 6$, otrzymamy 504). Wynika ona z faktu, że każde trzy wybrane karty można przearanżować na sześć różnych sposobów, podobnie jak w poprzednim przykładzie z trzema kolorowymi kulami.

Aby zakończyć nasze rozważania o permutacji i kombinacji, musimy wprowadzić podobny wybór elementów, ale tym razem z dozwolonymi powtórzeniami. Oznacza to, że za każdym razem po wybraniu elementu ze zbioru n różnych obiektów, odkładasz go z powrotem do tego zbioru. W przykładzie z kolorowymi kulami bierzesz jedną kulę z worka, zapamiętujesz jej kolor i odkładasz ją z powrotem do worka. Analogicznie, w drugim przykładzie z kartami, wybierasz jedną kartę, zapisujesz numer na tej kartce i odkładasz ją z powrotem do talii. W ten sposób możesz mieć np. dwie czerwone kule w swojej kombinacji lub 228 jako swoją permutację.

Zapewne domyślasz się, że oba wzory znacznie się przez to skomplikują. W rzeczywistości, w przypadku permutacji, równanie staje się jeszcze prostsze. Wzór na liczbę kombinacji z powtórzeniami jest następujący:

a na liczbę permutacji z powtórzeniami:

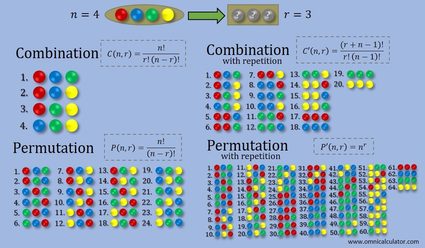
Na poniższym rysunku przedstawiamy zestawienie różnic pomiędzy czterema rodzajami wyboru obiektu: kombinacji, kombinacji z powtórzeniami, permutacji oraz permutacji z powtórzeniami. Jest to przykład, w którym masz cztery kule o różnych kolorach i wybierasz trzy z nich. W przypadku wyboru z powtórzeniami możesz wybrać jedną z kul kilka razy. Jeśli chcesz spróbować z permutacjami, uważaj! Bo będą to tysiące różnych możliwych zestawów. Jednak nadal możesz spokojnie obliczyć, ile ich jest (permutacje są w trybie zaawansowanym — Advanced mode).

Zacznijmy od prawdopodobieństwa kombinacji, niezbędnego w wielu problemach statystycznych. Przykład przedstawiony powyżej powinien to łatwo wyjaśnić — wybierasz z worka trzy z czterech kolorowych kul. Powiedzmy, że chcesz poznać szanse (prawdopodobieństwo), że wśród nich znajdzie się czerwona kula. Są cztery różne kombinacje, a czerwona kulka jest w trzech z nich. Prawdopodobieństwo kombinacji wynosi wówczas:

Jeśli wylosujesz z worka trzy losowe kule, to w 75% przypadków wyciągniesz czerwoną kulę. Do wyrażenia prawdopodobieństwa używamy zwykle znaku procentu.

Załóżmy teraz, że wybierasz jedną kulę, zapisujesz, jaki ma kolor i wkładasz ją z powrotem do worka. Jakie jest prawdopodobieństwo kombinacji, że dostaniesz co najmniej jedną czerwoną piłkę? To jest problem „kombinacji z powtórzeniami”. Z powyższego rysunku widać, że kombinacji jest w sumie dwadzieścia, a czerwona piłka jest w dziesięciu z nich, więc:

Czy to nie jest zaskakujące? Otóż nie powinno być! Kiedy oddajesz pierwszą kulę, np. niebieską, możesz ją wylosować również jako drugą i trzecią. Szanse na otrzymanie czerwonej kuli są więc zmniejszone. Analogiczne rozważania możesz przeprowadzić z permutacją. Spróbuj rozwiązać problem z workiem kolorowych kul: jakie jest prawdopodobieństwo, że twoja pierwsza wylosowana kula jest czerwona?

Powiedzmy, że nie ufasz nam i chcesz to sprawdzić sam. Losujesz trzy kule z czterech i sprawdzasz, czy jest wśród nich kula czerwona, czy nie (jak w pierwszym przykładzie z tego fragmentu artykułu). Powtarzasz ten proces jeszcze trzy razy i otrzymujesz czerwoną kulę tylko w jednym z czterech przypadków — $25$ przypadków. Zgodnie z teorią spodziewałeś się $75$. Co się stało? Cóż, tak właśnie działa prawdopodobieństwo! Istnieje coś takiego jak prawo wielkich liczb, które opisuje wynik wykonywania tego samego eksperymentu dużą liczbę razy. Jeśli powtórzysz losowanie np. sto razy, to będziesz znacznie bliżej $75$.

Co więcej, prawo wielkich liczb prawie zawsze prowadzi do standardowego rozkładu normalnego, który może opisywać np. inteligencję lub wzrost ludzi, z tzw. p-wartością. Chcesz dowiedzieć się więcej? Kalkulator rozkładu normalnego 🇺🇸 to miejsce, do którego najlepiej się udać!

Czy kiedykolwiek obiła ci się o uszy kombinacja liniowa? W rzeczywistości, mimo że zawiera słowo kombinacja, nie ma wiele wspólnego z tym, czego nauczyliśmy się do tej pory. Mimo to postaramy się ją krótko wyjaśnić. Kombinacja liniowa jest wynikiem wybrania zbioru elementów, wymnożenia każdego wyrazu przez pewną stałą liczbę i dodania otrzymanych wyników. Jest ona często używana w fizyce falowej do przewidywania równania siatki dyfrakcyjnej, a nawet w fizyce kwantowej ze względu na równanie de Broglie'a. Poniżej możesz zobaczyć kilka popularnych przykładów kombinacji liniowej:

1. Wektory. Każdy wektor w trzech wymiarach można rozłożyć na trzy wektory jednostkowe $\^e_1 = (1,0,0)$, $\^e_2 = (0,1,0)$ and $\^e_3 = (0,0,1)$. Na przykład $\vec{v} = (2,5,3) = 2\^e_1 + 5\^e_2 + 3\^e_3$ i to jest kombinacja liniowa.
2. Funkcje. Powiedzmy, że masz dwie funkcje $f(x) = \text{e}^x$ oraz $g(x) = \text{e}^{-x}$. Z tych dwóch funkcji można utworzyć kombinacje liniowe opisujące sinus hiperboliczny $\sinh(x) = \frac{f(x)}{2} - \frac{g(x)}{2}$ albo cosinus $\cosh(x) = \frac{f(x)}{2} + \frac{g(x)}{2}$. Podobną rzecz można zrobić z normalnym sinusem i cosinusem, ale trzeba użyć liczby urojonej $i$. Piszemy o tym więcej w ostatniej części kalkulatora pierwiastka kwadratowego 🇺🇸.
3. Wielomiany. Załóżmy, że masz trzy wielomiany $p_1(x) = 1$, $p_2(x) = 3x + 3$, $p_3(x) = x^2 -x + 1$ i chcesz wyrazić funkcję $q(x) = 2x^2 + x + 3$ jako kombinację liniową tych wielomianów. Nie zawsze jest to możliwe, ale w tym przypadku $q(x) = -2p_1(x) + p_2(x) + 2p_3(x)$.

Podstawową różnicą między kombinacjami a permutacjami w matematyce jest to, czy dbamy o kolejność elementów, czy nie:

• W permutacji kolejność ma znaczenie, więc układamy elementy w porządku sekwencyjnym.
• W kombinacjach kolejność nie ma znaczenia, więc wybieramy grupę elementów z większego zbioru.

Jeśli masz już kombinację i chcesz ją zamienić w permutację, to musisz narzucić kolejność na zbiór elementów, czyli wybrać jedno z możliwych uporządkowań dla twojego zbioru. Stąd liczba permutacji r elementów wybranych z n elementów jest równa liczbie kombinacji r elementów wybranych z n elementów pomnożonych przez liczbę uporządkowań tych r elementów, czyli przez r!.

Jeśli masz już permutację i chcesz ją zamienić w kombinację, to musisz usunąć kolejność, czyli traktować wszystkie możliwe podzbiory z takimi samymi elementami jako jeden podzbiór. Stąd liczba kombinacji r elementów wybranych z n elementów jest równa liczbie permutacji r elementów wybranych z n elementów podzielonych przez liczbę uporządkowań tych r elementów, czyli przez r!.

Jeśli słowo ma siedem różnych liter, to masz 7! = 5040 sposobów ich ułożenia (proste permutacje siedmiu elementów). Jeśli jednak niektóre litery występują więcej niż raz, to liczba wyrazów ulega zmniejszeniu! Na przykład:

• Jeśli słowo to „WALIZKA”, to mamy „A” występujące dwa razy, więc dzielimy 7! przez 2! = 2 i wynik to 2520.
• Jeśli słowo to „BABUNIA”, to mamy „B” i „A” pojawiające się dwa razy, więc dzielimy 7! przez 2! * 2! = 4 i wynik to 1260.
• Jeśli słowo to „SAŁATKA”, to mamy „A” występujące trzykrotnie, więc dzielimy 7! przez 3! = 6 i wynik to 840.