Kalkulator objętości półkuli

Omni kalkulator objętości półkuli szybko oblicza objętość półkuli za pomocą sześciu różnych równań. Potrzebujesz rozwiązać konkretny problem, ale nie wiesz, jak znaleźć objętość półkuli? Spróbuj wprowadzić jeden z parametrów i zobacz, jak sprawnie i szybko działa nasz kalkulator.

Fascynujesz się półkulami lub po prostu chcesz rozwiązać zadanie domowe? W dalszej części tekstu nauczymy się wszystkiego o właściwościach półkul oraz poznamy wzory na objętość półkul, z których korzysta nasz kalkulator. We wszystkich przypadkach potrzebujesz tylko jednej z poniższych wartości:

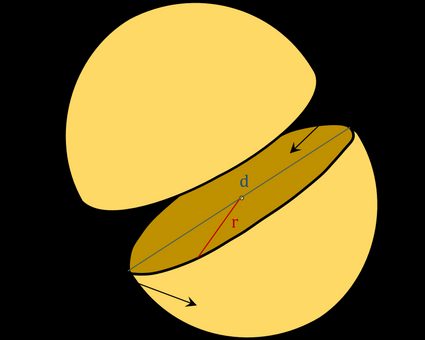
• $r$ - promień półkuli,

• $d$ — średnica półkuli;

• $V$ — objętość półkuli;

• $S$ — całkowite pole powierzchni półkuli;

• $S_p$ — pole powierzchni podstawy półkuli;

• $S_c$ — pole powierzchni kopuły półkuli; oraz

• $S/V$ — stosunkek powierzchni do objętości półkuli.

Jak sama nazwa wskazuje, półkula to część kuli podzielona na dwie równe połowy. Całkowite pole powierzchni każdej półkuli składa się z pola podstawy (okrąg) i pola powierzchni kopuły. Z jednej strony, suma pól powierzchni dwóch półkul nie jest taka sama jak pole powierzchni całej kuli, ale z drugiej strony, suma objętości dwóch kopuł jest równa objętości całej kuli.

Jeśli zakończyłeś/aś już obliczenia związane z półkulą, może zainteresuje cię nasz kalkulator kuli 🇺🇸, aby przeanalizować pełną sferę.

Najprostszym sposobem na oszacowanie objętości półkuli jest wyobrażenie sobie jej jako części pełnej kuli. Równanie na objętość kuli możesz znaleźć w naszym kalkulatorze objętości kuli. Jest ono wyrażone za pomocą promienia:

Dlatego wzór na objętość półkuli jest następujący:

Sytuacja jest nieco bardziej skomplikowana w przypadku pola powierzchni. Jeśli chcesz określić różnice między polem powierzchni kuli i półkuli, przejdź do kalkulatora pola powierzchni półkuli 🇺🇸. Krótko mówiąc, półkula ma dodatkowe pole podstawy, które należy wziąć pod uwagę podczas obliczeń.

Dzięki naszemu kalkulatorowi objętości półkuli możesz wykonywać obliczenia w wielu różnych jednostkach (w tym w jednostkach SI oraz imperialnych). Nie wahaj się i sprawdź nasze narzędzie do konwersji objętości 🇺🇸, aby dowiedzieć się więcej o różnych konwersjach jednostek!

Jak znaleźć objętość półkuli, gdy nie mamy podanego promienia? To zależy od tego, co wiesz o konkretnej półkuli. Nasz kalkulator objętości półkuli może obliczyć, na podstawie jednego wybranego parametru, wszystkie inne własności półkuli. Aby to wyjaśnić, zacznijmy od podania kilku podstawowych równań opisujących właściwości półkuli:

1. Średnica półkuli: $d = 2r$.

2. Objętość półkuli: $V = \frac{2}{3} \pi r^3$.

3. Pole powierzchni podstawy półkuli: $S_p = \pi r^2$.

4. Pole powierzchni kopuły półkuli: $S_c = 2 \pi r^2$.

5. Całkowite pole powierzchni półkuli: $S = 3 \pi r^2$.

6. Stosunek powierzchni do objętości półkuli: $S / V = 9 / (2 r)$.

Po kilku prostych przekształceniach algebraicznych, z powyższymi równaniami, możemy ostatecznie napisać sześć wzorów na objętość półkuli, które są używane przez nasz kalkulator objętości półkuli:

1. Dany promień: $V = \frac{2}{3} \pi r^3$.

2. Dana średnica: $V = \frac{1}{12} \pi d^3$.

3. Dane pole powierzchni podstawy: $V = \frac{2}{3} \sqrt{S_p^3 / \pi}$.

4. Podane pole powierzchni kopuły: $V = \frac{1}{3} \sqrt{S_c^3 / 2 π}$.

5. Podane całkowite pole powierzchni: $V = \frac{2}{9} \sqrt{S³ / 3 \pi}$.

6. Dany stosunek powierzchni do objętości: $V = 243 \pi / 4 (S/V)^3$.

Półkule możesz znaleźć w wielu aspektach naszego życia. Wiele otaczających nas obiektów ma kształt połowy kuli. W geografii i fizyce często mówimy, że Ziemia jest podzielona na dwie półkule: północną i południową. Czy wiesz, że kiedy podróżujesz samolotem, działa na ciebie „niewidzialna” siła, która powoduje odchylenie toru twojego kursu? Efekt ten nazywany jest efektem Coriolisa i zachowuje się inaczej na północnej oraz południowej półkuli Ziemi. Odwiedź stronę kalkulatora efektu Coriolisa 🇺🇸, aby dowiedzieć się więcej!