Kalkulator prawa Snelliusa

Kiedy światło przemieszcza się z jednego ośrodka do drugiego, ulega ugięciu lub załamaniu. Kalkulator prawa Snelliusa pozwoli ci szczegółowo zgłębić ten temat oraz zrozumieć zasady załamania światła. Czytaj dalej, aby dowiedzieć się, jak sformułowane jest prawo załamania Snelliusa, a także które równanie pozwoli ci obliczyć kąt załamania. Ostatnia część tego artykułu poświęcona jest formule i definicji kąta granicznego (krytycznego).

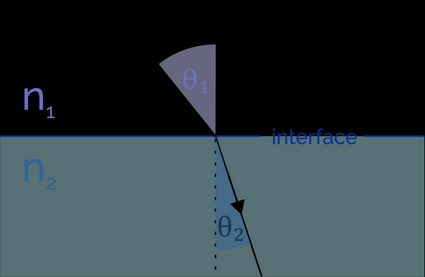
Prawo Snelliusa (znane też jako prawo Snella lub prawo załamania światła) opisuje, jak dokładnie działa załamanie światła. Kiedy promień światła wpada do innego ośrodka, zmienia się jego szybkość i długość fali. Kiedy fala przechodzi z ośrodka o większej prędkości rozchodzenia się do ośrodka o mniejszej prędkości, kąt załamania będzie mniejszy od kąta padania. W sytuacji odwrotnej, gdy prędkość się fali rośnie, kąt załamania jest większy od kąta padania. Kąt załamania zależy od współczynników załamania obu ośrodków:

gdzie:

• $n_1$ jest współczynnikiem załamania ośrodka 1 (z którego przemieszcza się promień)
• $n_2$ jest współczynnikiem załamania ośrodka 2 (do którego przemieszcza się promień)
• $\theta_1$ to kąt padania — kąt między linią normalną (prostopadłą) do granicy między dwoma ośrodkami a promieniem padającym
• $\theta_2$ to kąt załamania — kąt między normalną do granicy a promieniem przechodzącym przez ośrodek 2 (załamanym)

Możesz znaleźć niektóre wartości $n_1$ i $n_2$ dla popularnych mediów w kalkulatorze współczynnika załamania 🇺🇸.

Ogólnie rzecz biorąc, prawo załamania Snelliusa jest ważne tylko dla ośrodków izotropowych. W ośrodkach anizotropowych, takich jak kryształy, promień padający może zostać rozdzielony na dwa promienie (zjawisko dwójłomności).

Załóżmy, że chcesz znaleźć kąt załamania wiązki światła przechodzącej z powietrza do szkła. Kąt padania wynosi 30°.

1. Znajdź współczynnik załamania światła dla powietrza. Jest on równy $1,\!000293$.
2. Znajdź współczynnik załamania szkła. Załóżmy, że jest on równy $1,\!50$.
3. Przekształć równanie tak, aby niewiadoma (kąt załamania) znalazła się po lewej stronie: $\sin(\theta_2) = \frac{n_1 \sin(\theta_1)}{n_2}$.
4. Wykonaj obliczenia: $\sin(\theta_2) = \frac{1,000293 \sin(30\degree)}{1,50} = 0,\!333$.
5. Znajdź arcsin tej wartości: $\theta_2 = \arcsin(0,\!333) = 19,\!48 \degree$.
6. Możesz również zaoszczędzić trochę czasu i po prostu skorzystać z naszego kalkulatora prawa Snelliusa.

Czasami podczas stosowania prawa załamania otrzymasz $\sin(\theta_2)$ jako wartość większą niż 1. Jest to oczywiście niemożliwe. Jeśli tak się stanie, oznacza to, że całe światło jest odbijane od granicy ośrodków (zjawisko to znane jest jako całkowite wewnętrzne odbicie). Kalkulator prawa Snelliusa poinformuje cię, kiedy tak się stanie.

Najwyższy kąt padania, dla którego światło nie jest odbijane, nazywany jest kątem granicznym (lub krytycznym). Promień załamany przemieszcza się wzdłuż granicy obu ośrodków. Oznacza to, że kąt załamania jest równy 90°. W związku z tym możesz znaleźć kąt krytyczny, korzystając z poniższego równania:

Po uproszczeniu $n_1 \sin(\theta_1) = n_2 \cdot 1$.

Jeśli rozwiążesz to równanie dla danego kąta padania, otrzymasz, że: $\theta_1 = \arcsin(\frac{n_2}{n_1})$.