Kalkulator ugięcia belki
Omni kalkulator ugięcia belki pomoże ci określić maksymalne ugięcie belki dla belek swobodnie podpartych i wspornikowych przenoszących proste konfiguracje obciążenia.
Możesz wybierać spośród różnych typów obciążeń, które mogą oddziaływać na dowolną długość belki. Wielkość i lokalizacja tych obciążeń wpływa na stopień ugięcia belki.
W naszym kalkulatorze ugięcia belki poznasz różne wzory matematyczne ugięcia belki używane do obliczania ugięć belki swobodnie podpartej, jak również belki wspornikowej. Dowiesz się również, w jaki sposób moduł sprężystości belki i moment bezwładności jej przekroju poprzecznego wpływają na obliczone maksymalne ugięcie belki.
Ugięcie belki jest ważną częścią badań wytrzymałości, ale niemniej istotnym elementem jest analiza naprężeń występujących w belce pod wpływem zginania. Wskaźnik wytrzymałości przekroju na zginanie jest potężnym narzędziem do badania naprężeń zginających belki, które możesz obliczyć za pomocą naszego kalkulatora współczynnika wytrzymałości przekroju na zginanie 🇺🇸.
Co to jest ugięcie belki i zginanie belki?

W budownictwie zwykle używamy konstrukcji szkieletowych, które są utrzymywane w miejscu przez fundamenty znajdujące się w ziemi. Te konstrukcje szkieletowe są jak szkielety budynków, domów, a nawet mostów. W ramie, pionowe elementy ramy nazywamy kolumnami, a poziome belkami. Belki są wydłużonymi elementami konstrukcji, które przenoszą obciążenia pochodzące od poziomych płyt konstrukcji, takich jak lite betonowe podłogi, drewniane belki stropowe i dachy.
Gdy belki są pod wpływem zbyt dużych obciążeń, zaczynają się zginać. Odległość między odkształconą a nieodkształconą osią belki nazywamy ugięciem belki. To oznacza, że ugięcie belki jest pionowym przemieszczeniem punktu wzdłuż środka ciężkości belki. Możemy również rozważyć powierzchnię belki jako nasz punkt odniesienia, o ile nie ma zmian w wysokości lub głębokości belki podczas zginania.
Jak obliczyć maksymalne ugięcie belki
Wyposażyliśmy nasz kalkulator ugięcia belki we wzory, których używają inżynierowie oraz studenci kierunków technicznych, aby szybko określić maksymalne ugięcie, jakiego doświadczy określona belka z powodu przenoszonego przez nią obciążenia. Równania te mogą jednak rozwiązywać tylko proste obciążenia i kombinacje tych obciążeń. Poniżej przedstawiamy tabelaryczne zestawienie tych wzorów:
Wzory na ugięcie belki z prostym podparciem
Typy obciążenia belki | Równanie maksymalnego ugięcia belki () |
|---|---|
 | |
 | |
 | |
 | |
 | |
 |
Wzory na ugięcie belki wspornikowej
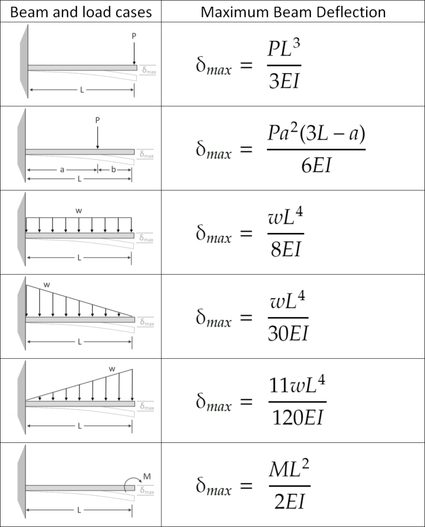
Zasada superpozycji
Aby obliczyć maksymalne ugięcie belki z kombinacją obciążeń, możemy użyć zasady superpozycji. Zasada superpozycji mówi, że możemy przybliżyć całkowite ugięcie belki, sumując wszystkie ugięcia wywołane przez każdą konfigurację obciążenia. Metoda ta daje nam jednak tylko przybliżoną wartość rzeczywistego maksymalnego ugięcia. Obliczanie skomplikowanych obciążeń wymagałoby użycia tak zwanej metody podwójnego całkowania.
Sztywność giętna belki
Do obliczenia ugięcia belki należy najpierw ustalić jej jej sztywność giętną (sztywność na zginanie), a także siłę obciążenia, która wpływa na zgięcie. Możemy zdefiniować sztywność belki, mnożąc jej moduł sprężystości, E, przez moment bezwładności jej przekroju poprzecznego, I.
Moduł sprężystości zależy od materiału, z którego wykonana jest belka. Im wyższy moduł sprężystości materiału, tym większe ugięcie może wytrzymać ogromne obciążenia, zanim osiągnie punkt krytyczny. Moduł sprężystości betonu wynosi od 15 do 50 GPa (gigapaskali), podczas gdy moduł sprężystości stali wynosi około 200 GPa i więcej. Ta różnica w wartościach modułu sprężystości pokazuje, że beton może wytrzymać tylko niewielkie ugięcie i pęknie szybciej niż stal.
Możesz dowiedzieć się więcej o module sprężystości, sprawdzając nasz kalkulator naprężeń 🇺🇸. Z drugiej strony, aby określić moment bezwładności określonego przekroju poprzecznego belki, możesz odwiedzić nasz kalkulator momentu bezwładności 🇺🇸. Moment bezwładności przekroju poprzecznego odpowiada wielkości oporu, jaki materiał stawia ruchowi obrotowemu, i zależy od wymiarów przekroju poprzecznego materiału.
Moment bezwładności przekroju zmienia się również w zależności od osi, wzdłuż której obraca się materiał. Aby lepiej zrozumieć to pojęcie, rozważmy przekrój poprzeczny prostokątnej belki o szerokości 20 cm i wysokości 30 cm. Korzystając ze wzorów, które możesz również zobaczyć w naszym kalkulatorze momentu bezwładności przekroju poprzecznego, możemy wykonać obliczenie w następujący sposób:
Iₓ = szerokość ⋅ wysokość³ / 12
Iₓ = 20 ⋅ (30³) / 12
Iₓ = 45 000 cm⁴
Iᵧ = wysokość ⋅ szerokość³ / 12
Iᵧ = 30 ⋅ (20³) / 12
Iᵧ = 20 000 cm⁴
Zauważ, że istnieją dwie wartości momentu bezwładności przekroju poprzecznego. Dzieje się tak, ponieważ możemy uznać, że belka ugina się pionowo wzdłuż przęsła belki (lub doświadcza momentu zginającego wokół osi x) i bocznie względem przęsła belki (lub ugina się wokół osi y). Ponieważ rozważamy ugięcie belki, gdy wygina się ona pionowo lub wokół osi x, musimy użyć Iₓ do naszych obliczeń.
Uzyskane przez nas wartości momentu bezwładności przekroju mówią nam, że belka jest trudniejsza do zginania przy obciążeniu pionowym i łatwiejsza do zginania, gdy jest poddawana poziomemu obciążeniu bocznemu. Ta różnica w wartościach momentu bezwładności jest powodem, dla którego widzimy belki w tej konfiguracji — gdzie ich wysokość jest większa niż szerokość.
Zrozumienie wzorów na ugięcie belki
Teraz gdy znamy już pojęcia modułu sprężystości i momentu bezwładności przekroju poprzecznego, możemy zrozumieć, dlaczego zmienne te są mianownikami w naszych wzorach na ugięcie belki. Wzory pokazują, że im sztywniejsza jest belka, tym mniejsze będzie jej ugięcie. Jednak analizując nasze wzory, możemy również stwierdzić, że długość belki również bezpośrednio wpływa na jej ugięcie. Im dłuższa jest belka, tym bardziej może się odkształcić i tym większe jest jej ugięcie.
Z drugiej strony, obciążenia wpływają na ugięcie belki na dwa sposoby: kierunek ugięcia i wielkość ugięcia. Obciążenia skierowane w dół mają tendencję do odchylania belki w dół. Obciążenia mogą mieć postać siły skupionej w punkcie, obciążenia ciągłego lub obciążenia momentem. Wzory w naszym kalkulatorze koncentrują się tylko na kierunku w dół lub w górę dla siły skupionej i obciążeń ciągłych. Obciążenia ciągłe są podobne do nacisku, ale uwzględniają tylko długość belki, a nie jej szerokość.
Równania w kalkulatorze uwzględniają również obciążenie chwilowe lub momentem obrotowym w kierunku zgodnym bądź przeciwnym do ruchu wskazówek zegara. Aby ustalić, w którym kierunku obciążenie ma wartość dodatnią, sprawdź kierunek strzałek na ilustracji odpowiadającej danemu wzorowi.
Przykładowe obliczenia ugięcia belki

Dla przykładowego obliczenia ugięcia belki rozważmy prostą drewnianą ławkę z nogami oddalonymi od siebie o 1,5 metra w ich środkach. Powiedzmy, że mamy deskę z sosny wschodniej o grubości 4 cm i szerokości 30 cm, która działa jako siedzisko tej ławki. Możemy uznać to siedzisko za belkę, która będzie się odchylać, gdy ktoś usiądzie na ławce. Biorąc pod uwagę wymiary tego siedziska, możemy obliczyć jego moment bezwładności przekroju poprzecznego, podobnie jak w naszym przykładzie powyżej. Ponieważ musimy obliczyć Iₓ, jego moment bezwładności wynosiłby:
Iₓ = szerokość ⋅ wysokość³ / 12
Iₓ = 30 ⋅ (4³)/12
Iₓ = 160 cm⁴ lub 1,6⋅10⁻⁶ m⁴
Wschodnia sosna biała ma moduł sprężystości 6800 MPa (6,8⋅10⁹ Pa), co jest wartością uzyskaną z . Możesz również łatwo uzyskać wartość modułu sprężystości dla innych materiałów, takich jak stal i beton, z internetu lub lokalnej biblioteki. Teraz gdy znamy już te wartości, zastanówmy się nad obciążeniem, jakie będzie przenosić ławka. Załóżmy, że na środku ławki siedzi dziecko, które wywiera nacisk 400 N (waży ok. 40 kg). Możemy teraz obliczyć ugięcie, jakiego dozna siedzisko ławki z powodu obciążenia punktowego w jego środku:
δmax = P ⋅ L³ / (48 ⋅ E ⋅ I)
δmax = (400 N) ⋅ (1,5 m)³ / (48 ⋅ 6,8⋅10⁹ Pa ⋅ 1,6⋅10⁻⁶ m⁴)
δmax = 0,002585 m = 2,585 mm
Oznacza to, że gdy dziecko usiądzie na środku ławki, siedzisko obniży się o około 2,6 milimetra w stosunku do pierwotnej pozycji.
Jeśli zainteresował cię ten temat i chcesz dowiedzieć się więcej o wytrzymałości materiałów, być może spodoba ci się również nasz kalkulator współczynnika bezpieczeństwa 🇺🇸.
FAQs
Czym jest ugięcie w inżynierii?
Ugięcie w inżynierii odnosi się do ruchu belki względem jej pierwotnej pozycji. Ruch ten może pochodzić od sił inżynieryjnych, albo od samego elementu konstrukcyjnego, albo od zewnętrznego źródła, takiego jak ciężar ścian lub dachu. Ugięcie w inżynierii jest miarą długości, ponieważ kiedy obliczasz ugięcie belki, otrzymujesz kąt lub odległość, która odnosi się do odległości ruchu belki.
Jaki jest ogólny wzór na ugięcie belki?
Ogólne wzory na ugięcie belki to PL³/(3EI) dla belek wspornikowych i 5wL⁴/(384EI) dla belek swobodnie podpartych, gdzie P to obciążenie punktowe, L to długość belki, E reprezentuje moduł sprężystości, a I odnosi się do momentu bezwładności przekroju poprzecznego. Jednak istnieje wiele innych wzorów, które pozwalają mierzyć różne typy belek i ugięć.
Jak obliczyć ugięcie belki?
Aby obliczyć ugięcie belki, wykonaj następujące kroki:
- Określ, czy jest to belka wspornikowa, czy belka swobodnie podparta.
- Zmierz ugięcie belki na podstawie deformacji konstrukcji.
- Wybierz odpowiedni wzór na ugięcie belki dla danego typu belki.
- Wprowadź dane, w tym długość belki, moment bezwładności przekroju poprzecznego, moduł sprężystości i działającą siłę.
Co powoduje ugięcie belek?
Głównymi przyczynami ugięcia są: ciężar umieszczony na górze konstrukcji, moment bezwładności przekroju poprzecznego, który jest rozmiarem przekroju poprzecznego, długość niepodpartej konstrukcji oraz materiał, z jakiego wykonana jest konstrukcja.
Jakie jest ugięcie środkowe belki swobodnie podpartej o rozpiętości 4 m?
3,47 mm, jeśli długość (L) wynosi 4 m = 4⋅10³ mm, obciążenie punktowe (P) wynosi 45⋅10³ N, moduł sprężystości (E) wynosi 2,4⋅10⁵ N/mm², a moment bezwładności przekroju poprzecznego (I) wynosi 72⋅10⁶ mm⁴. Aby to obliczyć:
- Wybierz wzór: PL³/(48EI).
- Wprowadź wartości:
45 ⋅ 10³ ⋅ (4 ⋅ 10³)³/(48 ⋅ 2,4 ⋅ 10⁵ ⋅ 72 ⋅ 10⁶) = 3,47 mm.
