Kalkulator objętości zbiornika

Dzięki naszemu kalkulatorowi objętości zbiornika możesz z łatwością oszacować objętość dowolnego zbiornika. Wybieraj spośród dziesięciu różnych kształtów pojemników: od standardowych zbiorników prostokątnych i cylindrycznych po zbiorniki kapsułowe i eliptyczne. Możesz nawet obliczyć objętość zbiornika w kształcie lejka (ściętego stożka). Po prostu wprowadź wymiary swojego zbiornika, a narzędzie obliczy jego całkowitą objętość. Możesz również podać wysokość, do której zbiornik ma zostać wypełniony. Ta wartość zostanie wykorzystana do obliczenia objętości napełnionego zbiornika.

Zastanawiasz się, jak zabrać się do tych obliczeń? Przewiń w dół, a znajdziesz wszystkie potrzebne wzory — na objętość zbiornika kapsułkowego, eliptycznego lub szeroko stosowanych zbiorników ze stożkowym dnem (czasami nazywanych zbiornikami stożkowymi), a także wiele innych!

Szukasz innych rodzajów zbiorników o różnych kształtach i do innych zastosowań? Sprawdź nasz kalkulator objętości, aby znaleźć objętość najpopularniejszych trójwymiarowych brył. Jeśli szukasz czegoś bardziej specjalistycznego, możesz również rzucić okiem na kalkulator akwarium i kalkulator objętości basenu, aby rozwiązać inne, nurtujące cię problemy.

Omni kalkulator objętości zbiornika to proste narzędzie, które pomoże ci znaleźć objętość zbiornika, a także objętość jego napełnionej części. Możesz wybrać jeden z dziesięciu kształtów zbiorników:

• cylinder pionowy,
• cylinder poziomy,
• prostopadłościan (pudełko),
• pionowa kapsuła,
• pozioma kapsuła,
• pionowy owalny (eliptyczny),
• poziomy owalny (eliptyczny),
• silos lejowy,
• silos płaskodenny, oraz
• ścięty stożek.

Ale jak używać naszego kalkulatora objętości zbiornika? Przyjrzyjmy się prostemu przykładowi:

1. Zadecyduj o kształcie. Załóżmy, że chcemy znaleźć objętość cylindra pionowego — wybierz tę opcję z rozwijanej listy. Schematyczny obraz zbiornika pojawi się poniżej; upewnij się, że jest to odpowiedni kształt.

2. Wpisz wymiary zbiornika. W naszym przypadku musimy wpisać długość oraz średnicę. Załóżmy, że wynoszą one odpowiednio $32\ \mathrm{cm}$ i $24\ \mathrm{cm}$. Dodatkowo możemy wprowadzić wysokość napełnienia — $28\ \mathrm{cm}$.

3. Kalkulator objętości zbiornika znalazł już objętość zbiornika oraz objętość cieczy po napełnieniu! Całkowita objętość zbiornika to $14,\!48\ \mathrm{litrów}$, a objętość cieczy wewnątrz to $12,\!67\ \mathrm{litrów}$. Jak zawsze, możesz zmienić jednostki w rozwijanej liście. Łatwizna!

Aby obliczyć całkowitą objętość cylindrycznego zbiornika, wszystko, co musimy wiedzieć, to średnica cylindra (lub promień) i wysokość cylindra (która może być nazywana długością, jeśli zbiornik leży poziomo).

Cylinder pionowy

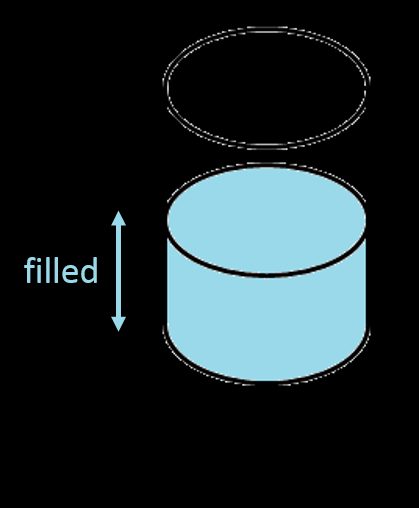
Możemy znaleźć całkowitą objętość zbiornika cylindrycznego za pomocą standardowego wzoru na objętość — pole podstawy pomnożone przez wysokość. Okrąg jest kształtem podstawy, więc jego pole, zgodnie z dobrze znanym równaniem, jest równe $\pi \cdot \mathrm{promień}^2$. Dlatego wzór na objętość pionowego zbiornika cylindrycznego wygląda następująco:

gdzie:

• $r$ — promień podstawy,
• $h$ — wysokość cylindra.

Jeśli chcemy obliczyć objętość wypełnionego zbiornika cylindrycznego, musimy znaleźć objętość cylindra pomniejszonego o niewypełnioną wysokość — to takie proste!

gdzie $f$ jest wysokością wypełnionej części cylindra.

Cylinder poziomy

Całkowitą objętość poziomego cylindrycznego zbiornika można znaleźć w analogiczny sposób — jest to powierzchnia jego okrągłej podstawy (tudzież ściany) pomnożona przez długość.

gdzie $l$ jest długością cylindra.

Sprawy komplikują się, gdy chcemy znaleźć objętość częściowo wypełnionego poziomego cylindra. Najpierw musimy znaleźć pole podstawy: pole odcinka koła pokrytego cieczą:

gdzie $r$ jest promieniem podstawy, a $\theta$ jest kątem środkowym odcinka. Kąt $\theta$ można znaleźć ze wzoru na cosinus:

gdzie $f$ jest wysokością wypełnionej części.

A więc:

dlatego wzór na objętość częściowo wypełnionego poziomego cylindra $V_{\scriptsize{\mathrm{fhc}}}$ jest następujący:

gdzie:

Jeśli zbiornik jest wypełniony w ponad połowie, łatwiej jest odjąć pustą część zbiornika od całkowitej objętości.

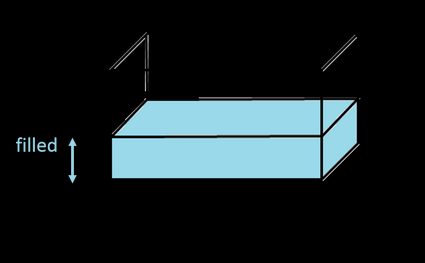
Jeśli zastanawiasz się jak obliczyć objętość zbiornika prostopadłościennego (znanego również jako prostopadłościan, pudełko lub kontener), nie szukaj dalej! Taki zbiornik niektórzy nazywają prostokątem — jednak nie jest to jego właściwa nazwa, ponieważ prostokąt jest kształtem dwuwymiarowym, więc nie ma objętości.

Aby znaleźć objętość graniastosłupa prostokątnego, pomnóż wszystkie wymiary zbiornika:

gdzie:

• $h$ — wysokość zbiornika,
• $s$ — szerokość,
• $l$ — długość zbiornika.

Jeśli chcesz wiedzieć, jaka jest objętość cieczy w zbiorniku, po prostu zmień zmienną wysokość na wypełniony we wzorze na objętość prostopadłościanu. Objętość napełnionego pojemnika, $V_{\scriptsize{\mathrm{rpf}}}$, wynosi:

gdzie $f$ jest wysokością wypełnionej części.

W naszym kalkulatorze nie ma znaczenia, czy zbiornik znajduje się w pozycji poziomej, czy pionowej. Upewnij się tylko, że wypełnienie i wysokość znajdują się wzdłuż tej samej osi.

Nasze narzędzie definiuje kapsułę jako dwie półkule oddzielone cylindrem. Aby obliczyć całkowitą objętość kapsuły, wszystko co musisz zrobić, to dodać objętość kuli do części cylindrycznej:

W zależności od położenia zbiornika, obliczenia objętości napełnienia będą się nieco różnić:

1. Dla poziomego zbiornika kapsułkowego

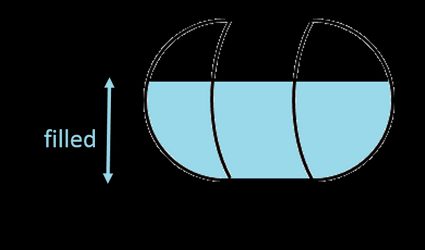
Ponieważ półkule na obu końcach zbiornika są identyczne, tworzą one kulistą nasadkę — dodaj tę część $V_{\scriptsize{\mathrm{sph\ hf}}}$ do części z poziomego cylindra $V_{\scriptsize{\mathrm{fhc}}}$ (sprawdź akapit powyżej), aby obliczyć objętość cieczy w wypełnionej poziomej kapsule ($V_{\scriptsize{\mathrm{kap\ hf}}}$):

gdzie:

• $d$ — średnica zbiornika;
• $f$ — wysokość napełnienia; oraz
• $\theta$ — kąt odpowiadający wypełnionej części w zbiorniku cylindrycznym, który w przekroju jest odcinkiem koła.

2. Dla pionowego zbiornika kapsułkowego

Wzór różni się dla różnych wysokości napełnienia. We wszystkich poniższych równaniach spotkamy się z następującymi wielkościami:

• $d$ — średnica zbiornika,
• $f$ — wysokość osiągnięta przez ciecz,
• $l$ — długość sekcji cylindrycznej.

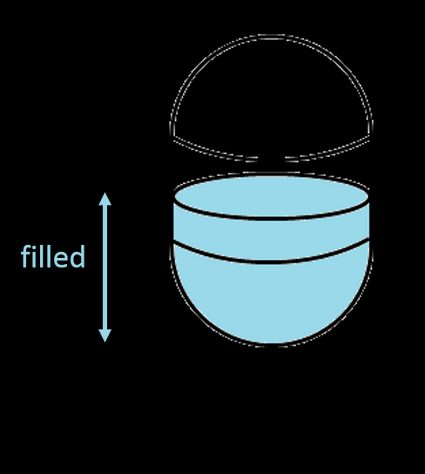
• Jeśli $f < d/2$, to ciecz znajduje się tylko w obrębie dolnej półkuli, więc potrzebujemy użyć jedynie wzoru na objętość cieczy w zbiorniku o kształcie półkuli:

• Jeśli $d/2 < f < d/2 +l$, musimy dodać objętość półkuli i odpowiedniej wysokości cylindra:

• Jeśli $d/2 + l < f$, oznacza to, że mamy pełną dolną półkulę i cylinder, więc musimy odjąć niewypełnioną część górnej półkuli od całkowitej objętości.

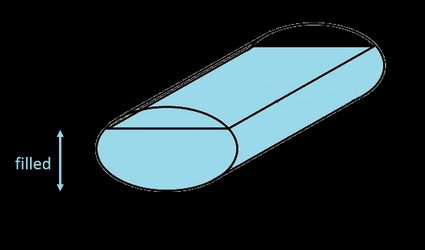
W naszym kalkulatorze definiujemy zbiornik owalny jako zbiornik cylindryczny o eliptycznym przekroju (nie w kształcie stadionu, jak jest to czasami definiowane). Aby znaleźć całkowitą objętość zbiornika eliptycznego, musisz pomnożyć obszar elipsy przez długość zbiornika:

gdzie:

• $s$ — szerokość zbiornika,
• $h$ — wysokość zbiornika,
• $l$ — długość zbiornika.

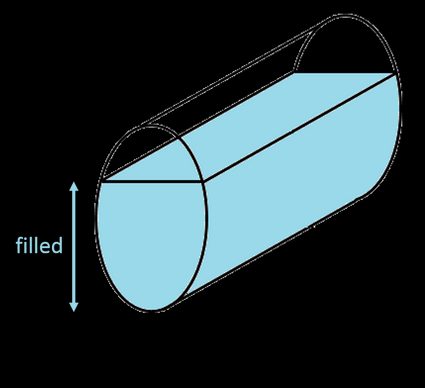
Wreszcie kolejny prosty wzór! Niestety, znalezienie objętości częściowo wypełnionego zbiornika — zarówno w pozycji poziomej, jak i pionowej — nie jest takie proste. Musimy użyć wzoru na odcinek elipsy i pomnożyć wynik przez długość zbiornika:

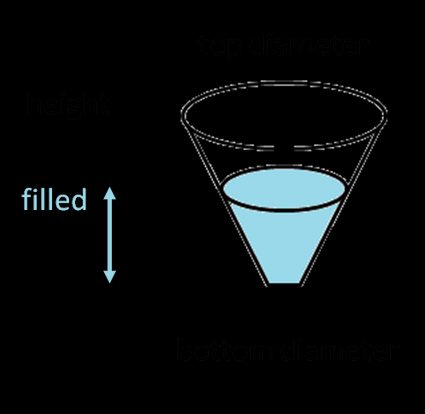
Aby obliczyć objętość stożka ściętego (szczególny kształt, który poznaliśmy w naszym kalkulatorze ściętego stożka 🇺🇸), użyj wzoru:

gdzie:

• $d_{\mathrm{góra}}$ — średnica górnej podstawy,
• $d_{\mathrm{dół}}$ — średnica dolnej podstawy,
• $h_{\mathrm{stożek}}$ — wysokość zbiornika.

Jeśli chcesz znaleźć częściowo wypełnioną objętość zbiornika w kształcie ściętego stożka dla danej wysokości wypełnienia, najpierw oblicz promień utworzony w miejscu do którego sięga materiał wypełniający zbiornik:

gdzie:

(Możesz wyprowadzić ten wzór z podobieństwa trójkątów)

Następnie znajdź objętość wypełnionego zbiornika:

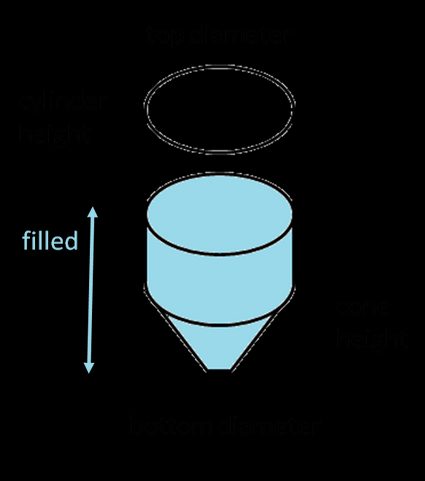
Znalezienie całkowitej objętości silosa lejowego nie jest takie trudne — po prostu dodaj objętość części ściętej do objętości części cylindrycznej:

gdzie:

• $d_{\mathrm{góra}}$ — górna średnica ściętego stożka,
• $d_{\mathrm{dół}}$ — dolna średnica ściętego stożka,
• $h_{\mathrm{stożek}}$ oraz $h_{\mathrm{cylinder}}$ — wysokości dwóch części tworzących silos.

Aby obliczyć częściowo napełniony zbiornik, po prostu zsumuj część ściętego stożka i część cylindryczną, w zależności od poziomu napełnionej cieczy, korzystając z powyższych równań.

Obliczanie całkowitej objętości silosa płaskodennego jest dokładnie takie samo jak w przypadku silosa lejowego. Jedyną różnicą jest kolejność wypełnienia — oczywiście najpierw napełniana jest część cylindryczna, a dopiero potem ściętego stożka.