Calcolatore per l'Intervallo di Confidenza

Questo calcolatore per l'intervallo di confidenza è uno strumento che ti aiuterà a trovare l'intervallo di confidenza per un campione, a condizione che tu fornisca la media 🇺🇸, la deviazione standard e la dimensione del campione. Puoi utilizzarlo con qualsiasi livello di confidenza arbitrario. Se vuoi sapere cos'è esattamente l'intervallo di confidenza e come calcolarlo o se stai cercando la formula dell'intervallo di confidenza al 95% per il punteggio Z, questo articolo ti aiuterà sicuramente.

La definizione dice che "un intervallo di confidenza è l'intervallo di valori, derivati dalle statistiche campionarie, che probabilmente contiene il valore di un parametro sconosciuto della popolazione". Ma cosa significa nella realtà?

Immaginiamo che un produttore di mattoni si preoccupi di verificare se la massa dei mattoni che produce sia in linea con le specifiche. Ha misurato che la massa media di un campione di 100 mattoni è pari a 3 kg. Ha anche scoperto che l'intervallo di confidenza del 95% è compreso tra 2,85 kg e 3,15 kg. Ciò significa che può essere sicuro al 95% che la massa media di tutti i mattoni che produce sarà compresa tra 2,85 kg e 3,15 kg. Più precisamente — se il produttore di mattoni prendesse tanti campioni di 100 mattoni e usasse ogni campione per calcolare l'intervallo di confidenza, il 95% di questi intervalli conterrebbe la vera massa media di un mattone.

Naturalmente, non sempre si vuole essere sicuri al 95%. Potresti voler essere sicuro al 99%, o forse è sufficiente che l'intervallo di confidenza sia corretto nel 90% dei casi. Questa percentuale è chiamata livello di confidenza.

Il calcolo dell'intervallo di confidenza richiede la conoscenza di tre parametri del campione: il valore medio, μ, la deviazione standard, σ, e la dimensione del campione, n (numero di misurazioni effettuate). Poi potrai calcolare l'errore standard 🇺🇸 e quindi il margine di errore secondo le seguenti formule:

Errore standard = σ/√n

Margine di errore = errore standard × Z(0,95)

dove Z(0,95) è il punteggio Z corrispondente al livello di confidenza del 95%. Se utilizzi un livello di confidenza diverso, devi calcolare il punteggio Z appropriato invece di questo valore. Ma non preoccuparti, il nostro calcolatore per il punteggio Z ti semplificherà le cose!

Come trovare il valore Z(0,95)? È il valore del punteggio Z in cui il livello di confidenza a due code è pari al 95%. Ciò significa che se si disegna una curva di distribuzione normale, l'area tra i due punteggi Z sarà pari a 0,95 (su 1).

Se vuoi calcolare questo valore utilizzando una tabella di punteggi Z, devi fare così:

1. Decidi il tuo livello di confidenza. Supponiamo che sia del 95%;

2. Calcola la probabilità che il tuo risultato non rientri nell'intervallo di confidenza. Questo valore è pari a 100% - 95% = 5%;

3. Guarda la curva della distribuzione normale. Il 95% è l'area centrale. Ciò significa che l'area a sinistra dell'opposto del tuo punteggio Z è pari a 0,025 (2,5%) e l'area a destra del tuo punteggio Z è anch'essa pari a 0,025 (2,5%); e

4. L'area a destra del tuo punteggio Z è esattamente uguale al valore p del tuo punteggio Z. Puoi utilizzare le tabelle dei punteggi Z per trovare il punteggio Z che corrisponde al valore p di 0,025. In questo caso, è 1,959.

Una volta calcolato il valore Z(0,95), puoi semplicemente inserire questo valore nell'equazione precedente per ottenere il margine di errore. Ora, l'unica cosa che resta da fare è trovare il limite inferiore e superiore dell'intervallo di confidenza:

Limite inferiore = media - margine di errore;

Confine superiore = media + margine di errore.

Per calcolare un intervallo di confidenza (a due lati), devi seguire i seguenti passaggi:

1. Supponiamo che la dimensione del campione sia di 100;

2. Trova il valore medio del tuo campione. Supponiamo che sia 3;

3. Determina la deviazione standard del campione. Supponiamo che sia 0,5;

4. Scegli il livello di confidenza. Il livello di confidenza più comune è il 95%;

5. Nella tabella statistica trova il punteggio Z(0,95), cioè il 97,5° quantile di N(0,1) — nel nostro caso è 1,959;

6. Calcola l'errore standard come σ/√n = 0,5/√100 = 0,05;

7. Moltiplica questo valore per il punteggio Z per ottenere il margine di errore: 0,05 × 1,959 = 0,098; e

8. Aggiungi e sottrai il margine di errore dal valore medio per ottenere l'intervallo di confidenza. Nel nostro caso, l'intervallo di confidenza è compreso tra 2,902 e 3,098.

Ecco fatto! Sono stati un bel po' di calcoli, vero? Fortunatamente, il nostro calcolatore per l'intervallo di confidenza è in grado di eseguire tutti questi calcoli da solo.

Un modo particolare di utilizzare gli intervalli di confidenza è l'analisi delle serie temporali, in cui l'insieme di dati campione rappresenta una sequenza di osservazioni in un intervallo di tempo specifico.

Un argomento frequente di questo tipo di studio è se una variazione di una variabile influisce su un'altra variabile in questione.

Per essere più specifici, consideriamo la seguente domanda generale che spesso suscita l'interesse degli economisti — "Come influisce una variazione del tasso di interesse sul livello dei prezzi?".

Esistono diversi modi per affrontare questo problema, che comportano una complessa analisi teorica ed empirica, che va ben oltre lo scopo di questo testo. Inoltre, esistono diverse tecniche per stimare e applicare gli intervalli di confidenza, ma con questo esempio possiamo rappresentare la funzionalità dell'intervallo di confidenza in un problema più complicato.

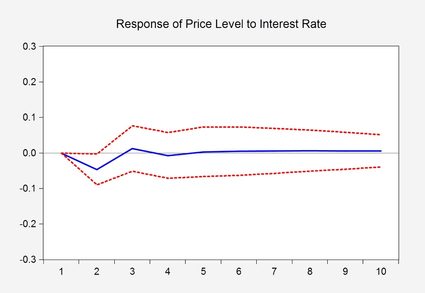
Il grafico qui sopra è una rappresentazione visiva di un risultato di stima di un modello econometrico, la cosiddetta funzione di risposta agli impulsi, che mostra la reazione di una variabile in caso di cambiamento dell'altra variabile. Le linee rosse tratteggiate sotto e sopra la linea blu rappresentano un intervallo di confidenza del 95% o, in un altro nome, una banda di confidenza, che definisce una regione di risultati più probabili. Più precisamente, mostra che dopo una variazione del tasso di interesse, è solo nel secondo mese che si verifica una risposta significativa a livello di prezzi.

In conclusione, ci auguriamo che con gli esempi e la breve descrizione di cui sopra tu abbia capito meglio lo scopo dell'intervallo di confidenza e che tu possa utilizzare il nostro calcolatore per l'intervallo di confidenza.

Se si estraggono ripetutamente dei campioni e si utilizza ognuno di essi per trovare un gruppo di intervalli di confidenza al 95% per la media della popolazione, la vera media della popolazione sarà contenuta in circa il 95% di questi intervalli di confidenza. Il restante 5% degli intervalli non conterrà la vera media della popolazione.

Il punteggio Z per un intervallo di confidenza bilaterale del 95% è 1,959, ovvero il 97,5° quantile della distribuzione normale standard N(0,1).

Il punteggio Z per un intervallo di confidenza a due lati del 99% è 2,807, ovvero il 99,5° quantile della distribuzione normale standard N(0,1).

L'ampiezza di un intervallo di confidenza aumenta quando il margine di errore aumenta, il che accade quando:

• Il livello di significatività aumenta;
• La dimensione del campione diminuisce; oppure
• La varianza del campione aumenta.

L'ampiezza di un intervallo di confidenza diminuisce quando il margine di errore diminuisce, il che accade quando:

• Il livello di significatività diminuisce;
• La dimensione del campione aumenta; oppure
• La varianza del campione diminuisce.

La media del campione non ha alcun impatto sull'ampiezza di un intervallo di confidenza!