Calcolatore per l'Area del Rettangolo

Se hai bisogno di conoscere l'area di un tappeto, di un pacco, di uno schermo televisivo, di una piscina rettangolare o di una finestra, questo calcolatore per l'area del rettangolo risolverà il tuo problema in un batter d'occhio!

Tutto quello che devi fare è inserire la lunghezza e la larghezza (o la diagonale) e permettere a questo calcolatore per l'area del rettangolo di trovare i valori di P (perimetro) e A (area).

Continua a leggere se vuoi capire cos'è un rettangolo, se sei interessato alla definizione di rettangolo, alle formule e alle proprietà di un rettangolo, oppure vuoi semplicemente imparare come trovare l'area di un rettangolo.

Un rettangolo è un quadrilatero con quattro angoli retti. Possiamo anche definirlo in altre parole come un parallelogramma contenente un angolo retto — se un angolo è retto, gli altri devono essere uguali. Inoltre, ogni lato di un rettangolo ha la stessa lunghezza di quello opposto. I suoi lati adiacenti non devono essere uguali, a differenza del quadrato, un caso particolare di rettangolo.

Se conosci un po' di latino, il nome di una forma di solito spiega molte cose. La parola rettangolo deriva dal latino rectangulus. È una combinazione di rectus (che significa "giusto, dritto") e angulus (angolo), quindi può essere una definizione semplice e basilare di rettangolo.

Il rettangolo è un esempio di quadrilatero. Puoi usare il nostro calcolatore per quadrilateri 🇺🇸 per trovare l'area di altri tipi di quadrilateri.

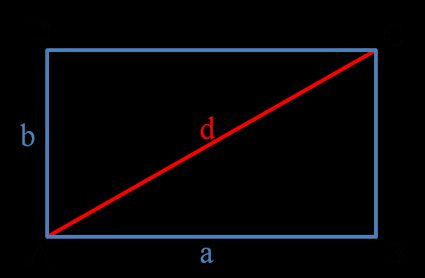
L'immagine qui sopra mostra un tipico rettangolo. Ha quattro lati e quattro angoli retti. Le lunghezze dei lati sono indicate con a e b, mentre la lunghezza della diagonale è indicata con d.

Se tutti i lati del rettangolo hanno la stessa lunghezza, lo chiamiamo quadrato.

L'area di un rettangolo è uno spazio limitato dai suoi lati, o, in altre parole, dal perimetro del rettangolo. Per trovare l'area di un rettangolo, basta moltiplicare i lati rettangolari a e b:

Area = a × b.

Il nostro calcolatore per l'area del rettangolo ha implementato le seguenti formule:

• Per l'area del rettangolo:
  A = a × b;

• Per il perimetro del rettangolo:
  P = 2 × (a + b); e

• Per la diagonale del rettangolo:
  d² = a² + b², o
  d = √(a² + b²).

Dato che conosciamo la formula dell'area del rettangolo A = a × b, mostriamo con un esempio come si può calcolare questa proprietà:

1. Scegli la lunghezza del rettangolo, ad esempio, a = 5 cm;
2. Decidi la larghezza del rettangolo — ad esempio, b = 6 cm;
3. Moltiplica questi due valori: A = 5 cm × 6 cm = 30 cm²; e
4. L'area del rettangolo è di 30 cm².

Scopriamo come trovare il perimetro di un rettangolo. Come al solito, il perimetro è la somma di tutti i lati di una forma:

P = a + b + a + b,

...che può essere scritto:

P = 2 × (a + b).

Prendiamo come esempio lo stesso rettangolo:

1. Scegli la lunghezza del rettangolo — a = 5 cm nel nostro caso;
2. Decidi la larghezza del rettangolo — ad esempio, b = 6 cm;
3. Aggiungi questi due valori — a + b = 5 + 6 = 11 cm;
4. Moltiplica il risultato per 2 —P = 2 × 11 = 22 cm; ed
5. Ecco fatto! Il perimetro del nostro rettangolo è di 22 cm.

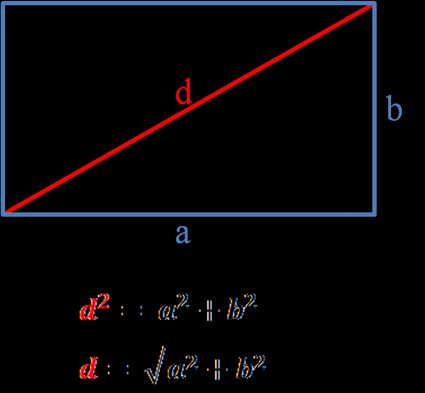
La diagonale del rettangolo è un segmento che collega due vertici opposti di un rettangolo. Calcoliamo la lunghezza della diagonale del rettangolo esemplare:

1. Scegli la lunghezza del rettangolo, ad esempio a = 5 cm;
2. Decidi la larghezza del rettangolo, ad esempio b = 6 cm;
3. Eleva a alla seconda — a² = 25 cm²;
4. Eleva b alla seconda —b² = 36 cm²;
5. Aggiungi questi due valori: a² + b² = 25 + 36 = 61 cm²;
6. Infine, prendi la radice quadrata del risultato: d = √(a² + b²) = √61 ~ 7,81 cm; e
7. La lunghezza della diagonale è di 7,81 cm.

Naturalmente, invece di calcolare manualmente tutti questi valori, puoi utilizzare questo calcolatore per l'area del rettangolo. Puoi anche utilizzarlo al contrario, ad esempio per calcolare la larghezza di un rettangolo con lunghezza e perimetro noti.

La figura qui sopra mostra un tipo speciale di rettangolo chiamato rettangolo aureo (scoprilo con il nostro calcolatore per il rettangolo aureo). Un rettangolo di questo tipo soddisfa la seguente condizione:

(a + b) / a = a / b = ϕ,

dove φ è il rapporto aureo pari a 1,618. Scopri di più su questo speciale rapporto con il nostro calcolatore per la sezione aurea.

Come probabilmente ricorderai dal calcolatore del rapporto 🇺🇸, un rapporto è una relazione tra due quantità, spesso rappresentata come una frazione.

Sapevi che puoi costruire il rettangolo aureo usando solo una riga e un compasso? Bastano pochi passaggi!

1. Disegna un quadrato;
2. Traccia una linea dal punto medio di un lato del quadrato all'angolo opposto. Il nostro calcolatore per il punto medio può aiutarti in questo passaggio;
3. Disegna un cerchio con un raggio pari alla linea e il centro nel punto medio, come nell'immagine qui sopra;
4. Il punto in cui il cerchio incontra il lato esteso del quadrato è l'angolo successivo del rettangolo aureo; e
5. Trova l'ultimo vertice e completa il rettangolo aureo.

Voilà! Facile, vero?

I rettangoli hanno molte proprietà interessanti, sono:

• Ciclici — significa che tutti gli angoli si trovano su un unico cerchio;
• Equiangolari — tutti gli angoli sono uguali a 90 gradi;
• Rettilinei — i suoi lati si incontrano ad angolo retto;
• Composti da due linee di simmetria riflessa — verticale e orizzontale attraverso il centro;
• Composti da due diagonali che si bisecano. Puoi trovare la lunghezza della diagonale utilizzando il teorema di Pitagora; e
• I lati opposti di un rettangolo sono paralleli tra loro e hanno la stessa lunghezza.

Altre proprietà dei rettangoli meno conosciute:

• L'intersezione delle diagonali è il circocentro — esiste un cerchio che ha il centro in quel punto e che passa per i quattro angoli;
• In un rettangolo con lati di lunghezza diversa (in parole povere, non un quadrato), non è possibile disegnare una circonferenza inscritta; e
• Le linee che uniscono i punti medi dei lati di un rettangolo formano un rombo, che è la metà dell'area del rettangolo. I lati della forma sono paralleli alle diagonali.

Puoi anche pensare tu stesso alle proprietà, ad esempio per quanto riguarda la rivoluzione di un rettangolo — lungo il lato o la diagonale per ottenere un cilindro o un cono, rispettivamente.

In poche parole:

1. Un quadrato è un rettangolo? Sì;
2. Un rettangolo è un parallelogramma? Sì;
3. Un rettangolo è un rombo? In generale — NO. Solo se è un quadrato (gli angoli del rombo sono tutti di 90 gradi);
4. Un rombo è un rettangolo? In generale — NO. Solo se è un quadrato (i lati del rettangolo sono tutti di lunghezza uguale);
5. Un rettangolo è un quadrilatero? Sì, ovviamente; e
6. Un rettangolo è un trapezio? Sì.

Ti stai chiedendo se un quadrato è un rettangolo o se un rettangolo è un parallelogramma? Dai un'occhiata all'immagine qui sotto e non avrai più dubbi sulle relazioni tra quadrilateri:

Come si legge questa tabella? Partiamo dal nostro rettangolo. Tre figure sono collegate direttamente alla forma — un quadrato, un parallelogramma e un trapezio isoscele. Quindi, se la forma si trova sopra la nostra forma di interesse, come il quadrato e il rettangolo. Possiamo dire che:

• Ogni quadrato è un rettangolo e un quadrato è un caso speciale di rettangolo.

Per le altre due figure, possiamo affermare analogicamente che:

• Ogni rettangolo è un parallelogramma e un rettangolo è un caso particolare di parallelogramma; e
• Ogni rettangolo è un trapezio e un rettangolo è un caso particolare di trapezio.

Esistono molte classifiche diverse che valutano i paesi in base alle loro aree, alla popolazione, al livello di istruzione o ai premi Nobel.

Ma ti sei mai chiesto chi è il vincitore della gara dei paesi più rettangolari? Un geostatistico australiano, David Barry, ha calcolato il parametro della rettangolarità per tutti i paesi del mondo e ha creato una classifica.

Ha scoperto che il paese più rettangolare è l'Egitto, mentre il titolo di "paese meno rettangolare del mondo" va alle Maldive (tuttavia, l'autore ammette che i calcolatori per i paesi composti da molte piccole isole potrebbero essere terribilmente sbagliati). Dai un'occhiata alla tabella qui sotto e controlla i primi dieci paesi e quelli meno rettangolari.

L'Egitto è in testa alla classifica, ma questo non dovrebbe sorprendere nessuno se si considera la forma del paese sulla mappa. Gli Stati Uniti si trovano a metà classifica, soprattutto a causa dell'eccentricità dell'Alaska e delle Hawaii. La cosa più confusa è che il secondo paese più rettangolare, il Vaticano, è allo stesso tempo il quarto paese più rotondo e la Polonia, quinta nella classifica delle rotondità, è nona nella classifica delle rettangolarità.

Come è possibile essere rettangolari e rotondi allo stesso tempo?! Come puoi intuire, è tutta una questione di definizione di rettangolarità e rotondità, che potrebbe non essere adeguata per forme complesse o disperse, e i confini dei paesi sono solitamente esempi di questo tipo, contenenti spigoli vivi, piccole isole o colonie da qualche parte nell'altra parte del globo.

Se sei interessato all'argomento, puoi dare un'occhiata a questa spiegazione e discussione dei risultati.

Si potrebbe pensare che il mondo sarebbe più facile da disegnare se ogni paese fosse un rettangolo... Oppure no?

La forma del rettangolo è utilizzata in molti schemi di tassellatura periodica. Può essere utilizzata per pareti di mattoni, piastrelle, pavimentazioni o mosaici vari. Di seguito troverai alcuni modelli popolari:

• Legame sovrapposto — È il modello di tassellatura più comune e più semplice, in quanto le piastrelle vengono posate in linee rette;

• Collegamento a scorrimento — Tipico delle pavimentazioni, delle piastrelle e dei mattoni;

• Spina di pesce — I pavimenti in legno si presentano bene con questo tipo di motivo; e

• Tessitura a cesto — Spesso utilizzata per corridoi o percorsi esterni.

Naturalmente le piastrelle sono disponibili in tutte le forme e dimensioni — esagono e ottagono con quadrati sono scelte molto popolari. Per quanto riguarda il pentagono, la forma deve essere irregolare per formare un disegno di piastrelle.

Il tipo di forma del corpo è uno dei problemi più ricercati legati ai rettangoli. Tutto ciò che devi fare è misurare il tuo busto, la vita, i fianchi e l'altezza dei fianchi e digitare i valori nello strumento. Otterrai così le informazioni sulla tua forma del corpo.

Ad esempio, la forma del corpo a rettangolo è definita come un tipo di corpo "maschile" — i fianchi, la vita e il busto hanno più o meno le stesse dimensioni. Il tuo corpo è ben proporzionato e di aspetto atletico.

Sorprendentemente, siamo circondati da oggetti rettangolari. Ecco perché il nostro calcolatore per rettangoli può essere utile non solo per le lezioni di matematica ma anche per i problemi di vita quotidiana. Naturalmente, non troverai un rettangolo ideale nella realtà, perché ha sempre una terza dimensione; ma se è piccolo rispetto alle altre due misure, l'approssimazione è sufficiente.

• Tavole a rettangolo— Date le dimensioni del tuo tavolo, puoi sapere quale tovaglia è necessaria o quanto pizzo o nastro per orli devi usare;

• Porte o vetri di finestre — Un temporale o una pallina da golf hanno rotto il vetro della tua finestra? Calcola l'area e stima il costo della riparazione, considerando il prezzo al metro quadro;

• Schermi di dispositivi elettronici, tablet, smartphone, TV — Usa questo calcolatore per l'area del rettangolo per stimare quanto spazio occuperà il tuo schermo sulla parete o quanto è grande lo schermo del telefono che vuoi acquistare; e

• Lavagne, specchi, cornici, tele, fogli di carta, quaderni, buste, soldi, bandiere, piscine rettangolari... La lista è infinita!

Dai un'occhiata. Riesci a trovare altri oggetti rettangolari intorno a te? Certo che sì!