Calcolatore di Crescita Esponenziale

Esiste un numero considerevole di processi per i quali è possibile utilizzare questo calcolatore di crescita esponenziale. La regola generale è che la formula di crescita esponenziale:

si usa quando c'è una quantità con un valore iniziale, $x_0$, che cambia nel tempo, $t$, con un tasso di variazione costante, $r$. La funzione esponenziale che compare nella formula sopra riportata ha una base pari a $1 + r/100$.

Nota che il tasso di crescita esponenziale, r, può essere qualsiasi numero positivo, ma questo calcolatore funziona anche come calcolatore per il decadimento esponenziale — dove r rappresenta anche il tasso di decadimento, che deve essere compreso tra 0 e -100%. Il motivo è che non si può avere un declino superiore al 100% rispetto alla quantità iniziale, poiché si otterrebbe un valore negativo.

L'equazione di crescita esponenziale viene utilizzata nella datazione al radiocarbonio 🇺🇸, nella PCR (puoi scoprire perché con il nostro calcolatore per la temperatura di ricottura 🇺🇸) e nel calcolo dell'interesse composto. Per saperne di più, consulta il nostro calcolatore di interesse composto. Per ulteriori esempi di utilizzo di questa formula, consulta le pagine seguenti.

Consideriamo il seguente problema; la popolazione di una piccola città all'inizio del 2019 era di 10 000 persone. Si è notato che la popolazione della città cresce a un tasso costante del 5% annuo. Cosa devi fare per calcolare la proiezione della popolazione nell'anno 2030? Dai dati forniti, possiamo concludere che il valore iniziale della popolazione, $x_0$, è pari a 10 000. Inoltre, abbiamo un tasso di crescita di $r = 5\%$.

Pertanto, la formula di crescita esponenziale che dovremmo utilizzare è:

Qui $t$ è il numero di anni trascorsi dal 2019. Nel nostro caso, per l'anno 2030, dovremmo utilizzare $t = 11$, poiché si tratta della differenza di anni tra il 2030 e l'anno iniziale 2019. Infine, otteniamo:

Quindi, il numero di abitanti previsto di nostra piccola città nell'anno 2030 è di circa 17 103.

Se vuoi approfondire questa particolare formula, puoi utilizzare il nostro calcolatore di crescita esponenziale per scoprire il numero di abitanti previsto per ogni anno, a partire dal 2019. Questo calcolo si traduce nella seguente tabella, in cui arrotondiamo i risultati al numero intero più vicino:

Se vuoi avere un'idea ancora più precisa della crescita della popolazione, puoi rappresentare questi dati graficamente, con l'asse orizzontale che rappresenta l'asse del tempo e l'asse verticale che rappresenta il valore della popolazione $x(t)$. I dati della tabella sono tutti punti che si trovano sul grafico continuo della funzione di crescita esponenziale:

Poiché la base di questa funzione esponenziale è 1,05 e poiché è maggiore di 1, il grafico di crescita esponenziale che otteniamo è crescente. La differenza principale tra questo grafico e quello della normale funzione esponenziale è che l'intersezione y non è 1, ma 10 000, che corrisponde al valore iniziale $x_0$:

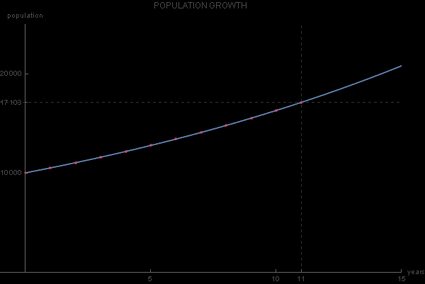
Da questo esempio, possiamo vedere i possibili limiti del modello di crescita esponenziale — è non realistico che il tasso di crescita rimanga costante nel tempo. In particolare, è difficile aspettarsi che il tasso di crescita annuale della popolazione della città rimanga al 5% per un decennio o più.

Nelle situazioni reali, ci sono oscillazioni naturali del tasso di crescita che non sono incluse in questo modello di crescita esponenziale. Un modello più realistico di crescita della popolazione è il modello di crescita logistica, che prevede la capacità di carico, una costante che rappresenta il limite naturale di crescita della popolazione.

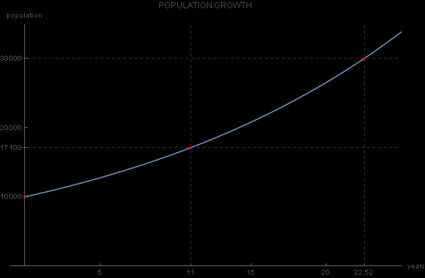
Continuando con la nostra piccola città, la domanda successiva che ti puoi porre è; "Quando possiamo aspettarci che la popolazione raggiunga un valore significativo?" Questo è utile se vuoi sapere quando adeguare la pianificazione urbanistica della città a una popolazione più numerosa, quindi il consiglio comunale deve sapere in quale anno può aspettarsi che la popolazione della città sia triplicata rispetto ai 10 000 abitanti iniziali?

In questo caso sappiamo quanto è $x(t)$, ma non conosciamo il valore di t quando questo accadrà. Procediamo per gradi:

1. Inserisci $x(t) = 30\ 000$ nella formula: $30\ 000 = 10\ 000 \times 1,\!05^{t}$

2. Dopo aver diviso entrambi i lati dell'equazione per 10 000, otteniamo: $1,\!05^{t} = 3$.

3. Prendi il logaritmo in base 1,05 di entrambi i lati dell'equazione: $t = \log_{1,05} 3$.

4. Usa il logaritmo per ottenere: $t = 22,\!52$.

Quindi, la risposta alla domanda del consiglio è circa 22 anni dopo l'anno iniziale del 2019, quindi nel 2041:

Potresti aver già notato un problema con la crescita e il decadimento esponenziali — il tempo viene naturalmente trattato solo come un valore positivo, quindi stiamo prevedendo una quantità futura. Tuttavia, questo non ci impedisce di utilizzare questa formula con valori temporali negativi. Ciò significa che descriviamo il fenomeno di interesse nel periodo precedente all'osservazione iniziale.

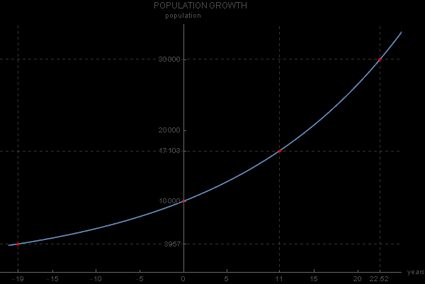
Nel caso della crescita della popolazione, puoi chiederti; qual è stata la popolazione della nostra piccola città nell'anno 2000, supponendo che il tasso di crescita della popolazione fosse costante al 5%?

Per risolverla, dovresti utilizzare $t = -19$, poiché l'anno 2000 precede l'anno 2019 di 19 anni. La risposta sarebbe quindi

abitanti, come si può vedere anche in questo grafico:

Per alcune applicazioni, ad esempio per il calcolo del decadimento esponenziale di una sostanza radioattiva, è più produttivo un modello alternativo per scrivere la formula della crescita e del decadimento esponenziale:

Il coefficiente $k$ svolge il ruolo di tasso di crescita, proprio come $r$ nella formula di crescita esponenziale originale. Confrontando l'equazione precedente con quella originale, si può notare che la relazione tra $r$ e $k$ è la seguente:

il che significa $r = 100 \times (e^k- 1)$ e $k = \ln(1 + r/100)$.

Il decadimento radioattivo è un noto esempio di utilizzo della formula del decadimento esponenziale. Per una data quantità iniziale di sostanza radioattiva, puoi scrivere la legge che regola il suo decadimento nel tempo. Ma forse un esempio più divertente è quello di misurare quanto caffè rimane nel tuo corpo alle 22:00 se hai bevuto una tazza di caffè con $x_0 = 95\: \rm{mg}$ di caffeina a mezzogiorno.

Utilizzeremo il fatto che il periodo di dimezzamento della caffeina nel corpo umano è di circa sei ore. L'emivita è definita come il tempo necessario a una data quantità per ridursi alla metà del suo valore iniziale. Quindi, in questo esempio abbiamo

$x(6) = 1/2 \times 95 \text{ mg} = 47,\!5 \text{ mg}$

In questo caso, sarà più facile utilizzare la notazione alternativa per la formula di crescita esponenziale:

$x(t) = 95 \times e^{kt}$.

Ecco il calcolo passo dopo passo:

1. Inserisci x(6)= 47,5 e t = 6 nell'equazione: $47,\!5 = 95 \times e^{6k}$.

2. Questa espressione, dopo aver diviso entrambi i lati dell'equazione per 95 e aver applicato il logaritmo naturale, dà: $6\times k = \ln 0,\!5$.

3. Utilizzando il logaritmo naturale, otteniamo: $k = -0,\!1155$.

4. Pertanto, la formula del decadimento esponenziale nel nostro esempio è: $x(t) = 95 \times e^{-0,1155 \times t}$.

5. Poiché le 22:00 sono dieci ore dopo il mezzogiorno, vogliamo conoscere la quantità di caffeina a $t = 10$. Abbiamo: $x(10) = 95 \times e^{-0,\!1155 \times 10} = 29,\!9305$.

Quindi, alle 22:00, la quantità di caffeina rimasta nel tuo corpo sarà di circa 30 mg.

Il tempo può essere espresso in qualsiasi unità di misura appropriata. Per alcuni problemi si tratterà di secondi, per altri di anni. Dovresti scegliere l'unità di tempo in modo che corrisponda alla natura del processo osservato. Ad esempio, se vuoi capire la variazione della popolazione di una città, dovresti scegliere gli anni. D'altra parte, se vuoi calcolare la quantità di caffè rimasta nel tuo corpo dopo averne bevuto una tazza, l'unità di tempo appropriata dovrebbe essere ore o forse minuti.

Tieni presente che $t$ non deve essere considerato solo come tempo. In alcuni casi, la variabile che misura il tasso di cambiamento può essere diversa dal tempo. Ad esempio, quando si studia il modo in cui la pressione atmosferica cambia con l'altitudine, la variabile che misura questo cambiamento è la distanza e dovresti scegliere i metri come unità di misura appropriata. Il nostro calcolatore per la pressione atmosferica ad alta quota può aiutarti in questo caso.

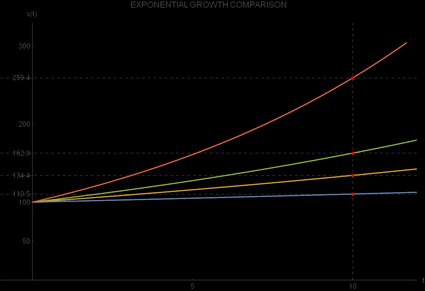
La differenza nel tasso di crescita esponenziale r avrà un'influenza significativa sulla velocità di variazione della quantità osservata rispetto al valore iniziale. Partiamo da $x_0 = 100$ e, usando il calcolatore di crescita esponenziale, vediamo quale sarà $x(10)$ per quattro diversi valori di $r$:

Da questa tabella, vediamo che tutti i valori iniziali sono uguali, essendo pari a $x_0 = 100$, ma i valori finali di $x(10)$ differiscono in modo significativo. Il tuo intuito potrebbe ingannarti perché la differenza tra l'1% e il 3% non sembra molto, ma dopo dieci periodi, questo equivale a un valore del 21,67% più alto per $x(10)$ con una crescita del 3% rispetto a quella dell'1%.

Se confronti la crescita del 10% con quella del 5%, noterai una differenza ancora maggiore, pari al 59,23% a favore della crescita del 10%. Puoi osservare questo contrasto nella seguente rappresentazione grafica delle quattro funzioni di crescita esponenziale:

La formula della crescita e del decadimento esponenziale è utilizzata per modellare diversi fenomeni del mondo reale:

• Crescita della popolazione di batteri, virus, piante, animali e persone;
• Decadimento della materia radioattiva;
• Concentrazione di farmaci nel sangue;
• Pressione atmosferica dell'aria ad una certa altezza;
• Interesse composto e crescita economica;
• Datazione al radiocarbonio; e
• Potenza di elaborazione dei computer, ecc.

• Come crescono le popolazioni: le equazioni esponenziali e logistiche [ENG]

  → (Clicca qui per approfondire questo argomento in italiano!)

• Due modelli di crescita della popolazione [ENG]

• La popolazione mondiale non cresce in modo esponenziale da almeno mezzo secolo [ENG]

  → (Clicca qui per approfondire questo argomento in italiano!)

• Crescita esponenziale della popolazione [ENG]

• Farmacologia della caffeina [ENG]

  → (Clicca qui per approfondire questo argomento in italiano!)

• [Effetti della caffeina sul sonno assunta 0, 3 o 6 ore prima di andare a letto] ENG

  → (Clicca qui per approfondire questo argomento in italiano!)