Calcolatore del Versore | Direzione del Vettore

Se vuoi calcolare la direzione di un vettore, sei nel posto giusto. Questo calcolatore del versore trova l'angolo di direzione di un vettore e calcola un vettore unitario in questa direzione. In questo contesto, il vettore unitario è chiamato versore.

I vettori sono uno strumento potente per rappresentare molte quantità fisiche nel nostro mondo fisico. Rappresentano forze, velocità e molte altre quantità derivate.

Oltre alla direzione, è possibile trovare anche il modulo del vettore se clicchi sulla Modalità avanzata del calcolatore. Pertanto, con questo strumento puoi trovare il modulo e l'angolo di direzione di qualsiasi vettore.

Puoi esprimere o calcolare la direzione di un vettore v in due modi:

1. Calcolando l'angolo di direzione del vettore v. L'angolo di direzione è l'angolo che v forma con l'asse x positivo, contando in senso antiorario; e
2. Ricavando un vettore unitario nella direzione dello stesso vettore. Questo vettore unitario è chiamato versore.

Per calcolare l'angolo $\theta$ che un vettore bidimensionale $\vec{v} = (x; y)$ forma con l'asse orizzontale, usa questa equazione:

L'unico problema di questa formula è che non ci fornisce l'angolo rispetto all'asse x positivo, ma rispetto all'asse orizzontale più vicino. Se il tuo vettore si trova nel primo quadrante del piano cartesiano, come il vettore che punta verso $P(3, 5)$ nell'immagine, questo non è un problema.

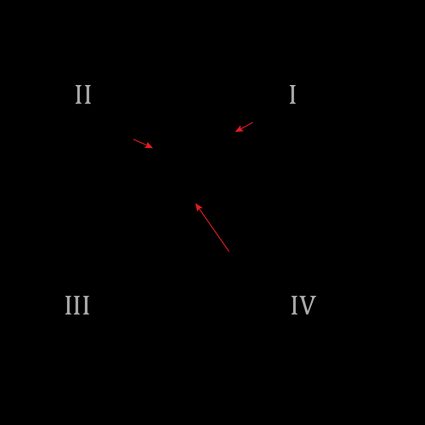
Ma cosa succede se un vettore appartiene a un altro quadrante? Supponiamo di voler trovare l'angolo di direzione $\theta$ del vettore $Q = (-2; 4)$ dell'immagine precedente. Se usassimo la formula precedente per trovare l'angolo di direzione, non otterremmo l'angolo corretto, poiché otterremmo l'angolo $\gamma$ invece dell'angolo di direzione $\theta$.

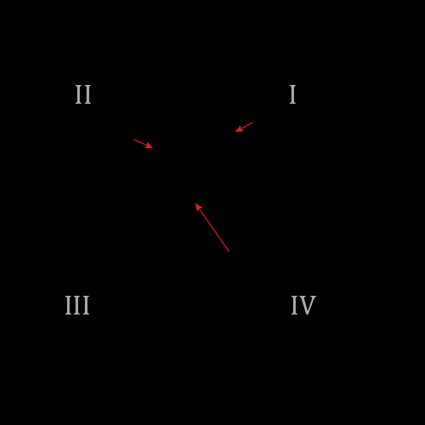
Come procedere?? Ebbene, in questo caso, avrai notato che $\theta = 180^\circ - \gamma$. Possiamo estendere questo ragionamento agli altri casi e trovare le seguenti equazioni per calcolare la direzione del vettore in ogni quadrante:

• Nel primo quadrante, $\theta_\text{I} = \arctan(\frac{y}{x})$;
• Nel secondo quadrante, $\theta_\text{II} = 180° - \arctan(\frac{y}{x})$;
• Nel terzo quadrante, $\theta_\text{III} = 180° + \arctan(\frac{y}{x})$; e
• Nel quarto quadrante, $\theta_\text{IV} = 360° - \arctan(\frac{y}{x})$.

Per ricavare un versore û nella direzione di un vettore v = (x, y, z), segui questi passaggi:

1. Trova il modulo di del vettore v:

   |v| = √(x² + y² + z²);

2. Dividi ogni coefficiente del vettore v per il modulo di v:

   û = v/|v| = (x/|v|; y/|v|; z/|v|); e

3. Questo è quanto. û è il versore di v, cioè il vettore unitario che va nella direzione di v.

Per ricavare un vettore con un modulo specifico nella direzione di un altro vettore v = (x, y, z):

1. Trova il modulo del vettore v:

   |v| = √(x² + y² + z²);

2. Trova un versore û nella direzione di v. Per farlo, dividi ogni coefficiente del vettore v per il suo modulo:

   û = v/|v| = (x/|v|; y/|v|; z/|v|); e infine

3. Moltiplica il modulo del vettore desiderato per il versore û. Il risultato sarà il vettore desiderato.

Per trovare il modulo e la direzione di due vettori, devi sommarli (puoi usare il nostro calcolatore per la somma dei vettori per farlo) e applicare a esso i passaggi descritti sopra.

Ora che sai come trovare il modulo e l'angolo di direzione di un vettore, vediamo alcuni esempi concreti e le domande frequenti.

Per ricavare un vettore con modulo 3 nella direzione di v = 12i - 5k:

1. Trova il modulo di v:

   |v| = √(12² + (-5)²) = 13;

2. Trova un versore û nella direzione di v. Per farlo, dividi v per il suo modulo:

   û = v/|v| = (12/13)i - (5/13)k; e infine

3. Moltiplica il modulo desiderato, 3, per il versore û. Otteniamo il vettore w:

   w = 3û = (36/13)i - (15/13)k.

   Esso ha la direzione e il modulo desiderati.

Per calcolare il versore nella direzione v = i + j + 2k:

1. Trova il modulo di v:

   |v| = √(1² + 1² + 2²) = √6 ≈ 2,4495;

2. Dividi il vettore v per il suo modulo:

   û = v/|v| = (1/√6)i + (1/√6)j + (2/√6)k; e

3. Questo è quanto. û è il versore nella direzione di v.

Il prodotto scalare di due vettori nella stessa direzione è sempre positivo. Questo perché il prodotto scalare di due vettori nella stessa direzione equivale alla moltiplicazione dei loro moduli, e il modulo di un vettore è sempre positivo.

Per trovare il modulo e la direzione della somma di due vettori:

1. Somma i due vettori;
2. Somma il quadrato di ogni componente del vettore ottenuto al punto 1;
3. Prendi la radice quadrata del risultato del punto 2: ecco il modulo della somma dei tuoi due vettori! ; e infine
4. Per calcolare la direzione del vettore v = (x; y), usa la formula θ = arctan(y/x), dove θ è l'angolo più piccolo che il vettore forma con l'asse orizzontale, e x e y sono le componenti del vettore ottenuto sommando i due vettori.