Ultimo aggiornamento: 07 Jul. 2024

Calcolatore per Triangoli Rettangoli Speciali

Q: 3, 4 e 5 sono una terna pitagorica?

Sì . I numeri interi a = 3 , b = 4 e c = 5 formano una terna pitagorica poiché a² + b² = c² e un triangolo con lati abc è un triangolo rettangolo speciale.

Creato da Dott. Hanna Pamuła, Ph.D.

Revisione eseguita da Bogna Szyk e Adena Benn

Adena Benn

LinkedInWebsite

Adena Benn is an Information Technology teacher with a degree in Computer Science. She has been teaching high schoolers since 1996 and loves everything computers. She loves problem-solving, so creating calculators to solve real-world problems is her idea of fun. She writes children's stories, is a seamstress, and is an avid reader. In her spare time, she travels and enjoys nature. See full profile

Check our editorial policy

Tradotto da Rangsimatiti Binda Saichompoo

Rangsimatiti Binda Saichompoo

With an environmental mind, Kat is currently pursuing a Master’s degree in Biomass Engineering and Bioeconomy. Kat joined Omni as an Italian and French translator. Apart from translating, writing content, and sometimes creating calculators, she loves nature, reading, sports, and playing lots of board games. See full profile

Check our editorial policy

e Agata Flak

Agata Flak

Linguistic freak at first sight, but VERY curious about numbers. Back in high school, she most enjoyed the satisfaction of getting the perfect result in a maths exercise or discovering something (not necessarily revolutionary) during a year-long project about cucumber hydrolysis. She can stay up far into the night, googling how much water there is in 400 ml of soup or how many ants it would take to make a car collapse under their weight. Weird, but oddly specific, and always highly meticulous. See full profile

Check our editorial policy

Nuovo

Indice

Triangoli rettangoli speciali 30 60 90 Triangoli rettangoli speciali 45 45 90 Altri triangoli rettangoli speciali Formule speciali per i triangoli rettangoli Regole speciali per il triangolo rettangolo Calcolatore per triangoli rettangoli speciali — esempio FAQ

Questo speciale calcolatore per triangoli rettangoli speciali ti aiuterà a risolvere le misure del triangolo scelto in un batter d'occhio. Seleziona il triangolo di cui hai bisogno e digita i valori indicati — i parametri rimanenti verranno calcolati automaticamente.

I triangoli rettangoli speciali sono triangoli rettangoli per i quali esistono formule semplici. Ciò consente di effettuare calcoli rapidi, quindi non è necessario utilizzare il teorema di Pitagora o qualche metodo avanzato. Scorri in basso per saperne di più sulle formule e le regole dei triangoli rettangoli speciali.

Triangoli rettangoli speciali 30 60 90

Il triangolo rettangolo speciale $30\degree$ $60\degree$ $90\degree$ è uno dei triangoli rettangoli più conosciuti. Le sue proprietà sono uniche perché è la metà del triangolo equilatero.

Triangolo rettangolo speciale: 30-60-90.

Se vuoi saperne di più su questa forma speciale, consulta il nostro apposito calcolatore per triangoli 30° 60° 90°.

Triangoli rettangoli speciali 45 45 90

Un altro famoso triangolo rettangolo speciale è il triangolo $45\degree$ $45\degree$ $90\degree$ . È l'unico triangolo rettangolo possibile che sia anche un triangolo isoscele. Inoltre, è la forma che si crea quando tagliamo il quadrato lungo la diagonale:

Triangolo rettangolo speciale: 45-45-90 con una data lunghezza del cateto.

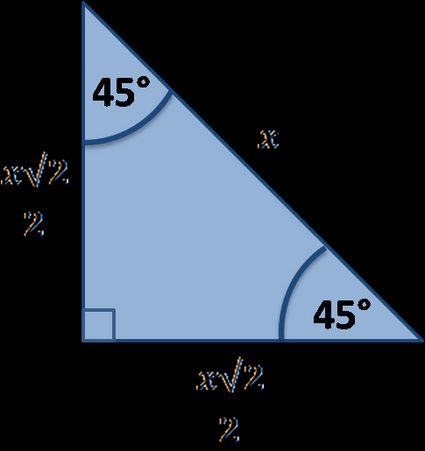
Triangolo rettangolo speciale: 45-45-90 con ipotenusa di lunghezza determinata.

Vorresti conoscere le proprietà di questo triangolo? Dai un'occhiata al nostro calcolatore per triangoli 45° 45° 90°.

Altri triangoli rettangoli speciali

Esistono molti triangoli rettangoli speciali, di seguito troverai quelli implementati nel nostro strumento:

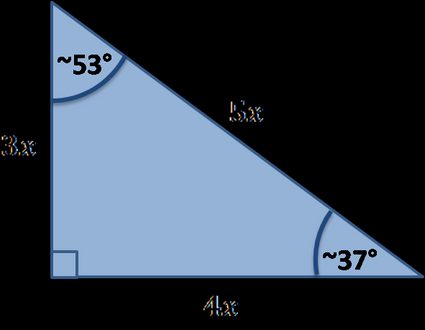
Triangolo rettangolo speciale: 3x-4x-5x.

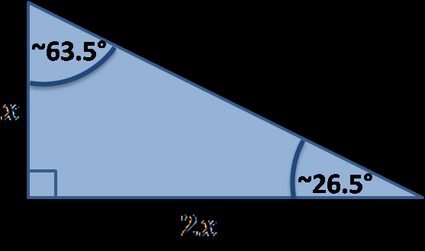
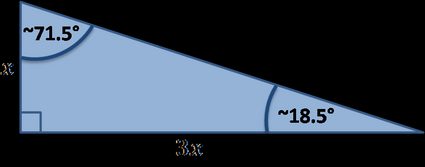
Formule speciali per i triangoli rettangoli

Triangolo rettangolo con lati a, b, c e angoli α, β.

Se stai cercando le formule dei triangoli rettangoli speciali, sei nel posto giusto. Guarda la tabella qui sotto; dovrebbe essere tutto chiaro! In questa tabella troverai le formule per la relazione tra angoli, cateti, ipotenusa, area e perimetro dei triangoli rettangoli speciali:

Triangolo rettangolo speciale	$a$ (cateto più corto)	$b$ (cateto più lungo)	$c$ (ipotenusa)	Area	Perimetro	Angolo $\alpha$	Angolo $\beta$
$30\degree$ - $60\degree$ - $90\degree$	$x$	$x\sqrt 3$	$2x$	$x^2\sqrt{3}/2$	$x(3+\sqrt3)$	$30\degree$	$60\degree$
$45\degree$ - $45\degree$ - $90\degree$	$x$	$x$	$x\sqrt 2$	$x^2/2$	$x(2+\sqrt 2)$	$45\degree$	$45\degree$
$x$ - $2x$	$x$	$2x$	$x\sqrt5$	$x^2$	$x(3+\sqrt 5)$	$\sim26,\!5\degree$	$\sim63,\!5\degree$
$x$ - $3x$	$x$	$3x$	$x\sqrt {10}$	$3x^2/2$	$x(4+\sqrt{10})$	$\sim18,\!5\degree$	$\sim71,\!5\degree$
$3x$ - $4x$ - $5x$	$3x$	$4x$	$5x$	$6x^2$	$12x$	$\sim37\degree$	$\sim53\degree$

Regole speciali per il triangolo rettangolo

I triangoli rettangoli speciali sono triangoli che hanno alcune caratteristiche specifiche che facilitano i calcoli. Naturalmente, la regola più importante per i triangoli rettangoli speciali è che devono avere un angolo rettangolo e una caratteristica in più. In generale, i triangoli rettangoli speciali possono essere divisi in due gruppi:

Triangoli rettangoli in base agli angoli — Ad esempio i triangoli $30\degree$ - $60\degree$ - $90\degree$ e $45\degree$ - $45\degree$ - $90\degree$ .
Triangoli rettangoli in base ai lati — Figure che hanno lati di lunghezza regolata da una regola specifica, per esempio:
- Lati con lunghezze intere chiamati terne pitagoriche:
  
  $3:4:5$ , $5:12:13$ , $8:15:17$ , $7:24:25$ , $9:40:41$ ;
- Lati con lunghezza intera ma quasi-isosceli:
  
  $20:21:29$ , $119:120:169$ , $696:697:985$ ; e
- Triangoli rettangoli i cui lati sono in progressione geometrica (triangolo di Keplero). È formato da tre lati di lunghezze uguali a quadrati perfetti. Le loro aree sono in progressione geometrica, secondo il rapporto aureo. Per saperne di più su questo speciale rapporto, visita il nostro calcolatore per la sezione aurea.

Ci sono molte regole e scelte diverse con cui possiamo scegliere il triangolo e definirlo speciale. Nel nostro calcolatore per triangoli rettangoli speciali, abbiamo implementato cinque triangoli scelti — due basati sugli angoli e tre sui lati.

Calcolatore per triangoli rettangoli speciali — esempio

Vediamo un esempio: vogliamo trovare la lunghezza dell'ipotenusa di un triangolo rettangolo se la lunghezza di un cateto è di $5$ centimetri e un angolo è di $45\degree$ .

Scegli il tipo corretto di triangolo rettangolo speciale. Nel nostro caso, si tratta del triangolo $45\degree$ - $45\degree$ - $90\degree$ ;
Inserisci il valore dato. Sappiamo che il lato è uguale a $5$ , quindi digitiamo questo valore nella casella a o b — non importa dove perché si tratta di un triangolo isoscele; e
Wow! Il calcolatore per triangoli rettangoli speciali ha risolto le misure del tuo triangolo!
- Il secondo cateto $b$ è uguale a $5\ \mathrm{cm}$ ,
- L'ipotenusa $c$ è $7,\!07\ \mathrm{cm}$ ,
- Il perimetro è uguale a $17,\!07\ \mathrm{cm}$ , e
- L'area del nostro triangolo speciale è $12,\!5\ \mathrm{cm^2}$ .

Non aspettare ancora. Provalo per conto tuo e dicci che ne pensi!

FAQ

Quali sono le formule per un triangolo 45 45 90?

Un triangolo 45 45 90 ha le seguenti formule, dove x è la lunghezza di uno qualsiasi dei lati uguali:

Ipotenusa = x√2;
Area = x²/2; e
Perimetro = x(2+√2).

Come si risolve un triangolo rettangolo speciale 30 60 90?

Per risolvere un triangolo rettangolo speciale di 30° 60° 90°, segui questi passaggi:

Trova la lunghezza del cateto più corto. La chiameremo x;
Il cateto più lungo sarà uguale a x√3;
L'ipotenusa sarà uguale a 2x;
L'area è A = x²√3/2; e
Infine, il perimetro è P = x(3 + √3).

Quali sono i due triangoli speciali della trigonometria?

I triangoli 30° 60° 90° e 45° 45° 90° (o triangolo isoscele) sono i due triangoli speciali della trigonometria. Sebbene esistano più di due triangoli rettangoli speciali, questi sono i più veloci da riconoscere e i più facili da lavorare. Un esempio di triangolo rettangolo speciale non basato sugli angoli è un triangolo rettangolo i cui lati formano una terna pitagorica.

3, 4 e 5 sono una terna pitagorica?

Sì. I numeri interi a = 3, b = 4 e c = 5 formano una terna pitagorica poiché a² + b² = c² e un triangolo con lati abc è un triangolo rettangolo speciale.