Calcolatore per il Perimetro

Q: Che cos'è il perimetro?

Il perimetro è il confine di una figura geometrica chiusa . Può anche essere definito come il bordo esterno di un'area, semplicemente la linea continua più lunga che circonda una forma. Il nome stesso deriva dal greco perimetros — peri che significa "intorno" + metron , inteso come "misura". Poiché si tratta della lunghezza del contorno della forma, viene espressa in unità di distanza, ad esempio metri, centimetri, piedi o pollici. Read more

Q: Posso determinare l'area dato il perimetro?

In generale, no , non è possibile calcolare l'area dal perimetro. Questo vale in particolare per rettangoli, parallelogrammi, aquiloni e trapezi. Tuttavia , per alcune forme specifiche, come i quadrati, gli esagoni, i poligoni regolari in generale e i cerchi, puoi determinare il loro lato (il raggio nel caso dei cerchi) dal perimetro e poi procedere al calcolo dell'area. Read more

Q: Qual è il perimetro di un edificio rettangolare di 20 m per 15 m?

Il perimetro è di 70 m . Per arrivare a questo risultato, devi sommare la lunghezza di tutti e quattro i lati dell'edificio. Due lati di lunghezza 20 m sommati danno 40 m, mentre gli altri due lati di lunghezza 15 m sommati danno 30 m. Insieme, otteniamo 40 m + 30 m = 70 m, come indicato. Read more

Con questo calcolatore per il perimetro non dovrai più preoccuparti dei calcoli del perimetro. Di seguito troverai le formule del perimetro per dodici forme diverse, oltre a un rapido promemoria su cos'è il perimetro e alla definizione di perimetro. Continua a leggere e prova, oppure dai un'occhiata al suo calcolatore gemello — il nostro completo calcolatore per l'area.

Che cos'è il perimetro?

Il perimetro è il confine di una figura geometrica chiusa. Può anche essere definito come il bordo esterno di un'area, semplicemente la linea continua più lunga che circonda una forma. Il nome stesso deriva dal greco perimetros — peri che significa "intorno" + metron, inteso come "misura". Poiché si tratta della lunghezza del contorno della forma, viene espressa in unità di distanza, ad esempio metri, centimetri, piedi o pollici.

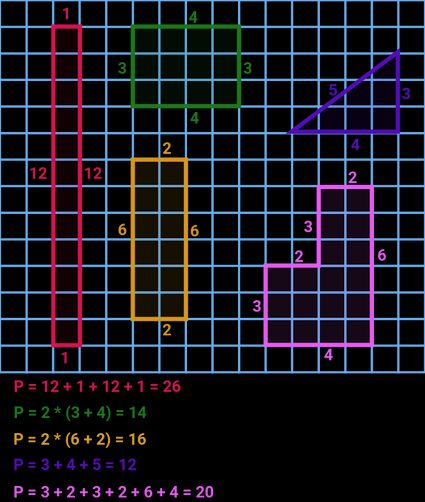
Come trovare il perimetro — Formule del perimetro

Di solito, l'approccio più semplice e diretto è quello di trovare la somma di tutti i lati di una forma. Tuttavia, ci sono casi in cui non ci sono lati (come nel caso di un'ellisse, di un cerchio, ecc.), oppure uno o più lati sono sconosciuti. In questo paragrafo elencheremo tutte le equazioni utilizzate in questo calcolatore per il perimetro.

Scorri le sezioni successive se ti interessa approfondire una forma specifica, e vuoi vedere la spiegazione e l'immagine per ognuna delle dodici forme presenti in questo calcolatore. Abbiamo anche degli strumenti dedicati a ciascuna forma — basta digitare il nome della forma nella barra di ricerca in alto su questa pagina web.

Ecco le formule del perimetro per le dodici forme geometriche presenti in questo calcolatore:

Formula del perimetro del quadrato: $P = 4a$ ;
Formula del perimetro del rettangolo: $P = 2(a + b)$ ;
Formule del perimetro del triangolo:
- $P = a + b + c$ ,
- $P = a + b + \sqrt{a^2 + b^2 - 2ab \times \cos(\gamma)}$ , o
- $P = a + \frac{a}{\sin(\beta + \gamma)} \times (\sin(\beta) + \sin(\gamma))$ ;
Formula del perimetro del cerchio: $P = 2\pi r$ ;
Formula del perimetro del settore circolare: $P = r(\alpha + 2)$ ( $\alpha$ è in radianti);
Formula del perimetro dell'ellisse: $P = \pi\bigl[3(a + b) - \sqrt{(3a + b) \times (a + 3b)}\bigl]$ ;
Formula del perimetro del quadrilatero / trapezio: $P = a + b + c + d$ ;
Formule del perimetro del parallelogramma:
- $P = 2(a + b)$ ,
- $P = 2a + \sqrt{2e^2 + 2f^2 - 4a^2}$ , oppure
- $P = 2(b + h/\sin(\alpha))$ ;
Vormule del perimetro del rombo:
- $P = 4a$ , oppure
- $P = 2\sqrt{e^2 + f^2}$ ;
Formula del perimetro di un aquilone: $P = 2(a + b)$ ;
Formula del perimetro di una corona circolare: $P = 2\pi(R + r)$ ; e infine
Formula del perimetro di un poligono regolare: $P = n \times a$ .

Formula del perimetro di un quadrato

Un quadrato ha quattro lati di uguale lunghezza. Per calcolare il suo perimetro, basta moltiplicare la lunghezza dei lati per $4$ :

\begin{split} P_\mathrm{{quadrato}} &= a+a+a+a\\ &=4a \end{split}

Che tu ci creda o no, abbiamo anche un calcolatore per il perimetro del quadrato 🇺🇸!

Formula del perimetro di un rettangolo

La formula del perimetro di un rettangolo è facile come l'equazione per il perimetro di un quadrato. L'unica differenza è che abbiamo due coppie di lati di uguale lunghezza:

\begin{split} P_\mathrm{{rettangolo}}& = a+b+a+b\\ &=2a+2b=2(a+b) \end{split}

Formula del perimetro di un triangolo

La formula più semplice per calcolare il perimetro del triangolo 🇺🇸 è, come sempre, la somma di tutti i lati:

P_{\mathrm{triangolo}} = a+b+c

triangolo, dati due lati e l'angolo tra di essi

Tuttavia, non sempre ti vengono dati tre lati. Cosa puoi fare allora? Invece di agitarti, puoi usare il calcolatore del teorema del coseno 🇺🇸 per trovare il lato mancante:

c=\sqrt{a^2+b^2-2ab\times\cos(\gamma)}

Questo può essere incorporato nella formula del perimetro:

\begin{split} &P_{\mathrm{triangolo}} = a+b\\ &+\sqrt{a^2+b^2-2ab\times\cos(\gamma)} \end{split}

triangolo, dati due angoli e un lato tra di essi

L'altra opzione è quella di utilizzare la legge dei seni se hai un lato e i due angoli adiacenti ad esso:

b = \sin(\beta)\times\frac{a}{\sin(\beta+\gamma)}

E:

c = \sin(\gamma)\times\frac{a}{\sin(\beta+\gamma)}

quindi il perimetro del triangolo può essere espresso come:

\begin{split} P_{\mathrm{triangolo}} &= a+\frac{a}{\sin(\beta+\gamma)}\\ &\times(\sin(\beta)+\sin(\gamma)) \end{split}

Formula del perimetro di un cerchio (formula della circonferenza)

Il perimetro di un cerchio ha un nome speciale — è noto anche come circonferenza. La formula del perimetro di un cerchio più conosciuta utilizza una sola variabile — il raggio del cerchio:

\mathrm{C} = 2\pi\times r

Ti domandi quante volte ruoterà la ruota della tua bicicletta in un tragitto di 10 km? Beh, questo è uno dei casi in cui dovrai usare la formula della circonferenza. Inserisci il raggio della tua ruota (metà del diametro della ruota) e dividi 10 km per la circonferenza ottenuta (ma non dimenticare la conversione delle unità di lunghezza!). Se vuoi maggior precisione, puoi includere le dimensioni del pneumatico della bicicletta.

Formula del perimetro di un settore circolare

Calcolare il perimetro di un settore circolare può sembrare complicato — si tratta solo della lunghezza dell'arco o della lunghezza dell'arco più due raggi? Tieni presente la definizione di perimetro! Il perimetro del settore è la somma delle lunghezze di tutti i suoi confini, quindi è la seconda:

P_{\mathrm{settore\ circolare}} = r\times(\alpha+2)

dove $\alpha$ è in radianti.

Formula del perimetro di un'ellisse (formula della circonferenza dell'ellisse)

Ellisse e assi semimaggiore e seminferiore

Sebbene la formula dell'area di un'ellisse sia davvero semplice e facile da ricordare, la formula del perimetro dell'ellisse è la più problematica di tutte le equazioni qui elencate. Abbiamo scelto di implementare una delle approssimazioni di Ramanujan in questo calcolatore per il perimetro:

\begin{split} &P_\mathrm{ellisse} = \pi\times\bigl(3(a+b)\\ &-\sqrt{(3a+b)\times(a+3b)}\bigr) \end{split}

Dove $a$ è il raggio più corto possibile e $b$ il raggio più lungo possibile dell'ellisse. L'altra approssimazione di Ramanujan, più precisa, è la seguente:

\begin{split} P_\mathrm{ellisse} =\ &\pi\times(a+b)\\ &\times\frac{1+3\frac{(a-b)^2}{(a+b)^2}}{10+\sqrt{4-3\frac{(a-b)^2}{(a+b)^2}}} \end{split}

Esiste anche una versione più semplice, che utilizza una variabile aggiuntiva $h$ :

h = \frac{(a-b)^2}{(a+b)^2}

Ovvero:

\begin{split} P_\mathrm{ellisse} =\ &\pi\times(a+b)\\ &\times\frac{1+3h}{10+\sqrt{4-3h}} \end{split}

Oppure puoi usare il nostro calcolatore!

Formula del perimetro di un trapezio

Se vuoi calcolare il perimetro di un trapezio irregolare, non c'è una formula speciale — basta sommare i quattro lati:

P_{\mathrm{trapezio}} = a+b+c+d

Forse l'hai notato, ma è la formula per il perimetro di qualsiasi quadrilatero.

C'è anche un'opzione che si presenta con alcuni trapezi speciali, come il trapezio isoscele, per il quale sono necessari i lati $a$ , $b$ e $c$ . Un altro esempio è il trapezio retto, dove la lunghezza delle basi e del lato obliquo sono sufficienti per trovare il perimetro della forma (per trovare l'ultimo lato, si utilizza il Teorema di Pitagora).

Formula del perimetro di un parallelogramma

In questo calcolatore per il perimetro troverai tre formule per calcolare il perimetro di un parallelogramma:

La più semplice consiste nel sommare tutti i lati:

\quad\ \ \begin{split} P_{\mathrm{parallelogramma}} &= a+b+a+b\\ &=2(a+b) \end{split}

Parallelogramma, dati un lato e le diagonali

La formula del perimetro di un parallelogramma che richiede un lato e le diagonali:

\quad\ \ \begin{split} &P_{\mathrm{parallelogramma}} = 2a\\ &\qquad \ \ \ +\sqrt{2e^2+2f^2-4a^2} \end{split}

Parallelogramma, data la base, l'altezza e qualsiasi angolo del parallelogramma

Il perimetro è dato in termini di base, altezza e qualsiasi angolo del parallelogramma:

\ \ \ P_{\mathrm{parallelogramma}} = 2\left(b+\frac{h}{\sin(\alpha)}\right)

Formula del perimetro di un rombo

Non serve l'astrofisica per calcolare la formula del perimetro di un rombo, quindi cerchiamo di essere sintetici — è la stessa formula del perimetro di un quadrato!

P_{\mathrm{rombo}} = 4a

Un'altra soluzione per trovare il perimetro del rombo richiede la lunghezza delle diagonali:

P_{\mathrm{rombo}} = 2\times\sqrt{e^2+f^2}

Prova a ricavare la formula i autonomia. Sai che le due diagonali di un rombo sono perpendicolari e si bisecano tra loro, quindi puoi dividere la forma in quattro triangoli rettangoli congruenti. Ogni triangolo ha cateti lunghi e/2 e f/2 — tutto ciò che devi fare è trovare l'ipotenusa del triangolo, che è allo stesso tempo il lato del rombo. Poi moltiplica il risultato per quattro per trovare il perimetro finale della formula del rombo.

Formula del perimetro di un aquilone

La formula per il perimetro di un aquilone è piuttosto semplice — basta sommare tutti i lati:

\begin{split} P_{\mathrm{aquilone}} &= a+a+b+b\\ &=2(a+b) \end{split}

Formula del perimetro di una corona circolare

Corona circolare, dati i raggi del cerchio esterno e del cerchio interno

Poiché il perimetro è definito come il confine, una corona circolare richiede di aggiungere la circonferenza di entrambi i cerchi concentrici:

\begin{split} P_{\text{corona circolare}} &= 2\pi \times R+2\pi\times r\\ &=2\pi\times (R+r) \end{split}

Formula del perimetro di un poligono (pentagono regolare, esagono, ottagono, ecc.)

Poligono regolare, data la lunghezza del lato e il numero di lati

Nel nostro calcolatore per il perimetro, abbiamo anche implementato una semplice formula per il perimetro di un poligono regolare:

P_{\mathrm{poligono}}=n\times a

dove $n$ è il numero di lati del poligono. Quindi, ad esempio, puoi calcolare il perimetro di un pentagono, di un esagono o di un ottagono.

Inoltre, per i poligoni fino a 12 lati, il nome del poligono viene visualizzato nello strumento. Fantastico!

Se vuoi determinare il perimetro di qualsiasi poligono, somma le lunghezze di tutti i suoi lati:

P_{\mathrm{poligono}} = \sum a_i

dove $a_1$ , $a_2$ , ..., $a_n$ sono le lunghezze dei lati e $\sum$ è il simbolo di somma (da $i = 1$ a $n$ ).

Oppure utilizza le coordinate dei vertici:

\begin{split} P_{\mathrm{poligono}} = &\sum_{i=1}^n\Bigl((x_{i-1}-x_i)^2\\ &\qquad +(y_{i-1}-y_i)^2\Bigr) \end{split}

Con $x_{n+1}=x_1$ e $y_{n+1}=y_1$ .

FAQ

Come si calcola il perimetro delle forme irregolari?

Per trovare il perimetro di una figura irregolare:

Misura la lunghezza di tutti i lati (esterni);
Se i lati includono frammenti circolari, misura il raggio e l'angolo centrale, cioè l'angolo tra i raggi che uniscono i due estremi dell'arco al centro;
Applica la formula della circonferenza del cerchio per questo raggio e prendi la parte proporzionale all'angolo; e
Somma la lunghezza di tutti i lati.

Posso determinare l'area dato il perimetro?

In generale, no, non è possibile calcolare l'area dal perimetro. Questo vale in particolare per rettangoli, parallelogrammi, aquiloni e trapezi. Tuttavia, per alcune forme specifiche, come i quadrati, gli esagoni, i poligoni regolari in generale e i cerchi, puoi determinare il loro lato (il raggio nel caso dei cerchi) dal perimetro e poi procedere al calcolo dell'area.

Qual è il perimetro di un edificio rettangolare di 20 m per 15 m?

Il perimetro è di 70 m. Per arrivare a questo risultato, devi sommare la lunghezza di tutti e quattro i lati dell'edificio. Due lati di lunghezza 20 m sommati danno 40 m, mentre gli altri due lati di lunghezza 15 m sommati danno 30 m. Insieme, otteniamo 40 m + 30 m = 70 m, come indicato.