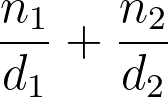Calcolatore di Frazioni

Benvenuti nel nostro calcolatore di frazioni, uno strumento davvero versatile. Può:

• ➕ sommare;
• ➖ sottrarre;
• ✖️ moltiplicare; e
• ➗ dividere due frazioni qualsiasi.

Inoltre, ha la capacità di semplificare una frazione (ovvero di ridurla), oltre a dirti come trasformare una frazione in un decimale e viceversa. Se non sei ancora impressionato, questo strumento non solo funziona con le frazioni standard corrette e improprie, ma anche con le frazioni miste — cosa vuoi di più? 😁

Come al solito, abbiamo preparato alcune letture introduttive che ti permetteranno di addentrarti nel mondo delle frazioni 🌎. Qui di seguito troverai la definizione di frazione, i tipi di frazioni (proprie, improprie, miste) e tutte le operazioni di base sulle frazioni semplici e miste. Siamo pronti?

Una frazione rappresenta il numero di parti uguali di un elemento intero.
Puoi riconoscere una frazione semplice perché presenta due numeri separati da una linea (o barra):

• Il numero superiore viene chiamato numeratore e viene scritto sopra la linea. Ci dice:

  Quante parti abbiamo.

• Chiamiamo il numero inferiore denominatore e lo scriviamo sotto la riga. Significa:

  Il numero totale di pezzi.

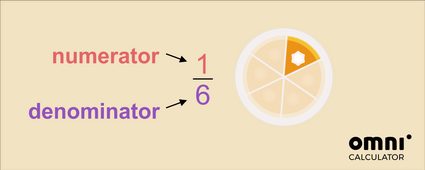
Nell'esempio precedente, si tratta di una parte delle sei fette in cui è stata tagliata la torta. Si legge come un sesto dell'intera torta.

Ma, ovviamente, la torta può essere tagliata in modo diverso!

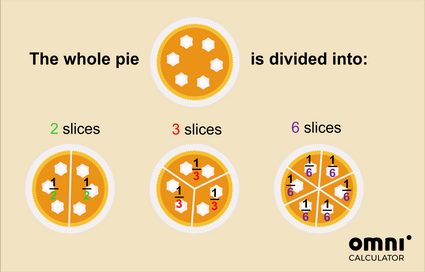
Quindi, se tagli la torta in due parti, una fetta corrisponde alla metà dell'intera torta. Se tagli la torta in 3 parti, allora una fetta corrisponde a un terzo dell'intera torta, etc.

Le frazioni sono utilizzate ovunque:

• Ogni volta che vuoi esprimere una parte di un oggetto intero, che può essere diviso in pezzi pari come una torta 🍰, una barretta di cioccolato 🍫, un'anguria 🍉, una pizza 🍕, etc;

• Quando misuriamo qualcosa 📏, soprattutto in metri o otto di metri; e

• La dimensione dello schermo del tuo computer 🖥️ è espressa come un rapporto, ad esempio 16:9 — ed è anche una frazione, solo scritta in modo diverso. (Per informazioni su come semplificare i rapporti, dai un'occhiata al nostro calcolatore del rapporto 🇺🇸!

Quindi, ora che conosci la definizione di frazione, diamo un'occhiata ai diversi tipi di frazione. In generale, esistono tre tipi di frazioni: le frazioni proprie, le frazioni improprie e le frazioni apparenti:

1. Frazioni improprie

   Nelle frazioni proprie, il numero superiore (numeratore) è più piccolo del numero inferiore (denominatore). Ciò significa che sarà sempre inferiore a un intero, ad esempio:

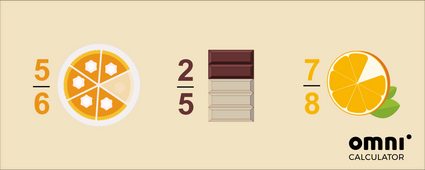
   🍰 5 fette di torta su una torta che è stata tagliata in 6;

   🍫 2 file di una tavoletta di cioccolato su un'intera tavoletta di cioccolato che ha 5 file; e

   🍊 7 parti di un'arancia su un'intera arancia che abbiamo tagliato in 8.

La regola generale, che vale sia per i numeri positivi che per quelli negativi, è che il valore assoluto della frazione sia inferiore a uno:

|^numeratore/_denominatore| < 1.

2. Frazioni improprie

   Che cos'è una frazione impropria? È una frazione in cui il numeratore è maggiore (o uguale) al denominatore. Le frazioni improprie sono talvolta chiamate frazioni pesanti. Esempi di frazioni improprie sono:

   🍰 10 fette di torta, quando ogni torta ha 6 fette;

   🍫 8 file di una tavoletta di cioccolato. Una tavoletta di cioccolato intera ha 5 file; e

   🍊 21 parti di arancia, se tagliamo ogni arancia in 8 pezzi uguali.

3. Frazioni apparenti

   Le frazioni apparenti, note anche come frazioni misti o numeri misti, sono un altro modo di esprimere una frazione impropria. Si tratta di numeri interi (il numero di cose intere) e di una frazione vera e propria messi insieme. Vediamo quindi gli esempi del paragrafo precedente:

   🍰 10 fette di torta, quando ogni torta ha 6 fette è uguale a → 1 torta intera e 4 fette su 6;

   🍫 8 file di cioccolato quando l'intera tavoletta di cioccolato ha 5 file → 1 tavoletta di cioccolato intera e 3 file su 5; e

   🍊 21 parti di arancia, se tagliamo l'arancia a 8 fette → 2 arance intere e cinque fette su 8.

Quando si tratta di sommare frazioni, ci sono tre scenari:

1. Il denominatore (numero inferiore) è lo stesso in entrambe le frazioni — ad esempio, ³/₅ e ¹/₅ .

   Questo è il caso più semplice; tutto ciò che devi fare è sommare i numeratori (numeri superiori) e lasciare il denominatore così com'è, ad esempio:

   ➽ ³/₅ + ¹/₅ = ^{(3 + 1)}/₅ = ⁴/₅ ;

2. Le frazioni hanno denominatori diversi — ad esempio, ²/₅ e ³/₁₀.

   Questo è un caso un po' più complicato — per sommare queste frazioni, devi trovare il denominatore comune.

   • Puoi usare, ad esempio, l'm.c.m. — il minimo comune multiplo per trovare il numero comune dei due denominatori: mcm(5,10) = 10 Un'altra opzione è quella di moltiplicare i denominatori e ridurre la frazione in un secondo momento.

   • In seguito, dovrai espandere ogni frazione in modo che il denominatore comune sia il numero inferiore:

   Quindi, devi moltiplicare la frazione con il denominatore uguale a 5 (il nostro 1/5) per 2 per ottenere 10 (ricorda che devi moltiplicare sia il numero superiore che quello inferiore):

   ➽ ²/₅ = ^{(2 × 2)}/_{(5 × 2)} = ⁴/₁₀ .

   La seconda frazione ha già un denominatore uguale a 10:

   ➽ ³/₁₀ .

   • Ora che le frazioni hanno lo stesso denominatore, puoi sommarle:

     ➽ ⁴/₁₀ + ³/₁₀ = ^{(4 + 3)}/₁₀ = ⁷/₁₀ .

3. Vuoi sommare due frazioni miste — ad esempio, 2 ³/₅ e 1 ¹/₂ .

   Una soluzione per questo tipo di problema è quella di convertire la frazione apparente in una frazione impropria e sommarla come al solito.

   Convertiamola per 2 ³/₅:

   • Moltiplica il numero intero per il denominatore:

     2 × 5 = 10 ;

   • Aggiungi il risultato al numeratore:

     10 + 3 = 13 ;

   • Questo è il tuo nuovo numeratore — scrivilo sopra il denominatore:

     2 ³/₅ = ¹³/₅.

   Analogamente, puoi scoprire che 1 ¹/₂ = ³/₂ ;

   • Esegui l'addizione standard di frazioni con denominatori disuguali:

     ➽ ¹³/₅ + ³/₂ = ²⁶/₁₀ + ¹⁵/₁₀ = ⁴¹/₁₀ ; e

   • Infine, puoi convertire il risultato in una frazione mista:

     Esegui la divisione lunga con un resto:

     ➽ ⁴¹/₁₀ = 4 R 1 = 4 ¹/₁₀ .

Naturalmente, il nostro calcolatore di frazioni si occupa di tutti questi scenari. 😎

Se ti stai ancora chiedendo come funziona l'addizione di frazioni, forse questa immagine può aiutarti?

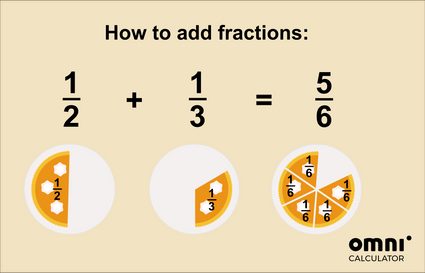
Per una spiegazione ancora più approfondita, dai un'occhiata al nostro calcolatore per la somma delle frazioni 🇺🇸.

Se ti stai chiedendo come si sottraggono le frazioni e hai letto la sezione precedente Come si sommano le frazioni — Regole per l'addizione delle frazioni, abbiamo una buona notizia per te: è praticamente la stessa cosa!

1. Se hai frazioni con lo stesso denominatore, sottrai i numeratori:

   ➽ ³/₅ - ¹/₅ = ^{(3 - 1)}/₅ = ²/₅ ;

2. Quando si sottraggono frazioni con nominatori diversi — ²/₅ e ³/₁₀ — ripeti la procedura della sezione precedente, ma sottraendo e non aggiungendo nel passaggio finale:

   • Trova un denominatore comune: è 10, e

   • Espandi le frazioni in frazioni equivalenti con un denominatore comune: ⁴/₁₀ e ³/₁₀ .

   • Sottrai i numeratori.

     ➽ ²/₅ - ³/₁₀ = ⁴/₁₀ - ³/₁₀ = ¹/₁₀ ;

3. Per le frazioni apparenti (2³/₅ e 1 ¹/₂):

   • Cambia le frazioni miste in frazioni improprie, come in precedenza:

     2 ³/₅ = ¹³/₅ e 1 ¹/₂ = ³/₂ ,

   • Sottrai le due frazioni improprie con denominatori disuguali:

     ➽ ¹³/₅ - ³/₂ = ²⁶/₁₀ - ¹⁵/₁₀ = ¹¹/₁₀ , e

   • Lasciala in una frazione impropria o riconvertila in una frazione mista:

     ➽ ¹¹/₁₀ = 1 R 1 = 1 ¹/₁₀ .

Puoi immaginare la sottrazione come una sottrazione o una mangiazione di una parte della torta:

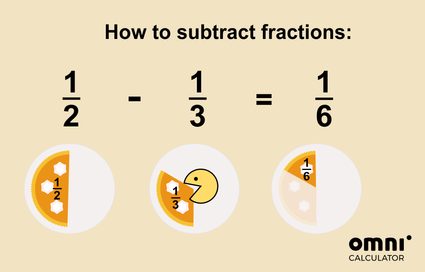
Non è stato così difficile, vero?

Moltiplicare le frazioni è un'operazione fortunatamente semplice. Si tratta di numeratore per numeratore più denominatore per denominatore. A volte è necessario semplificare la frazione. E questo è tutto!

Dai un'occhiata a questo esempio:

➽ ²/₃ × ⁵/₆ = ^{(2 × 5)}/_{(3 × 6)} = ¹⁰/₁₈ ,

che può essere semplificato in ⁵/₉ .

Ogni volta che hai a che fare con frazioni apparenti, non dimenticare che devi sempre scriverle come numero improprio prima di moltiplicarle:

➽ 2 ¹/₂ × 3 ¹/₄ = ⁵/₂ × ¹³/₄ = ^{(5 × 13)}/_{(2 × 4)} = ⁶⁵/₈ = 8 ¹/₈ .

E quando moltiplichi una frazione per un numero intero, ricorda che possiamo scrivere il numero intero come se stesso diviso per 1:

➽ 3 × ⁵/₇ = ³/₁ × ⁵/₇ = ^{(3 × 5)}/_{(1 × 7)} = ¹⁵/₇ .

Se non sai come affrontare la riduzione delle frazioni, scorri alla sezione Come si semplificano le frazioni?.

Ora che sai come moltiplicare le frazioni, passiamo all'argomento successivo; la divisione di frazioni.

Ti stai scervellando su come dividere le frazioni? Non preoccuparti! La divisione di frazioni è molto simile alla moltiplicazione di frazioni. L'unica differenza è che devi moltiplicare il primo numero per il reciproco della seconda frazione. Può sembrare un po' strano, ma è davvero semplice! Dai un'occhiata a questo esempio:

(¹/₂) / (³/₅) = ¹/₂ × ⁵/₃ = ^{(1 × 5)}/_{(2 × 3)} = ⁵/₆ .

Quindi, tutto ciò che devi fare è ribaltare la seconda frazione (che è il suo reciproco) e moltiplicare le frazioni. A volte potrebbe essere necessario ridurre le frazioni. E questo è tutto, tadaaa! 🎉

Ci piace sempre semplificare la nostra vita, anche in matematica. Ecco perché semplificare le frazioni è molto importante. Significa che scriviamo la frazione nella sua forma più semplice possibile. Le frazioni semplificate si chiamano anche riduzioni di frazioni.

Ma cosa significa esattamente? Dai un'occhiata a questi esempi:

• Preferiresti dire che è rimasto un quarto della pizza, invece di due otto, vero?
• Oppure che è stata mangiata metà di una torta e non tre sesti.

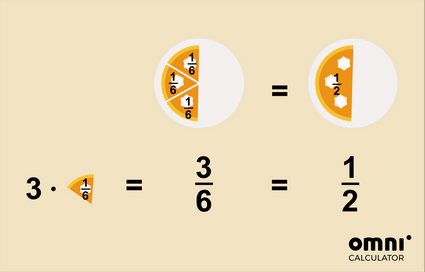
Per semplificare una frazione, puoi utilizzare due metodi:

1. Utilizzare una sorta di approccio a forza bruta — dividi la frazione per 2, 3, 5, 7, 11... fino a quando è impossibile continuare la divisione (senza un resto):

   ➽ ⁴²/₁₂₆ = /:2 ,

   ➽ ²¹/₆₃ = /:3 ,

   ➽ ⁷/₂₁ = /:7 ,

   ➽ ¹/₃ .

2. Trova l'MCD — massimo comune divisore del numeratore e del denominatore, e poi dividili per questo numero: MCD(42,126) = 42, quindi

   ➽ ⁴²/₁₂₆ = /:42 ,

   ➽ ¹/₃ .

Per saperne di più sulla riduzione delle frazioni, consulta il nostro calcolatore per semplificare le frazioni 🇺🇸. Inoltre, dai un'occhiata al nostro fantastico calcolatore per frazioni equivalenti 🇺🇸, che può trovare molti equivalenti alla tua frazione.

Se vuoi scoprire come convertire un decimale in una frazione, sei nel posto giusto. Ecco una guida passo a passo.

Supponiamo che tu voglia convertire 0,32 in una frazione:

1. Tratta il decimale come un numeratore. Il denominatore sarà quindi 1;

2. Sposta il punto decimale a destra, finché non avrai un numero intero:

   0,32 → 3,2 → 32 

   Ogni spostamento corrisponde alla moltiplicazione per 10

   0,32 × 10 → 3,2 × 10 → 32 ;

3. Hai moltiplicato il numeratore per 10 × 10 e ora dobbiamo moltiplicare il denominatore per lo stesso numero:

   1 × 10 × 10 = 100 ;

4. Hai trasformato la frazione in un decimale! ✨ 0,32 → ³²/₁₀₀ ; e

5. Infine, semplifica il risultato. Poiché il fattore comune maggiore tra 32 e 100 è 4, dividi sia il numeratore che il denominatore per questo valore:

   ➽ ³²/₁₀₀ = ⁸/₂₅ .

Ed ecco la frazione nella sua forma più semplice. ❤️

Il modo più semplice per trasformare una frazione in un decimale è quello di usare una calcolatrice. Che sia questo calcolatore di frazioni, una normale calcolatrice tascabile o il nostro strumento dedicato — il convertitore da frazione a decimale 🇺🇸.

A volte la frazione è relativamente facile da trasformare in decimale senza l'ausilio di alcuno strumento, come nel caso di 1/2, 3/4 (o anche 1/8). Crediamo che tu possa capire come espandere le frazioni di cui sopra in modo che il denominatore sia rispettivamente 10, 100, 1000 e così via:

• Moltiplica ¹/₂ per 5 per ottenere 10 come denominatore:

  ➽ ¹/₂ = ⁵/₁₀ = 0,5 ;

• Moltiplica ³/₄ per 25 per ottenere 100 come denominatore:

  ➽ ³/₄ = ⁷⁵/₁₀₀ = 0,75 ; e

• Moltiplica ¹/₈ per 125 per ottenere 1000 come denominatore:

  ➽ ¹/₈ = ¹²⁵/₁₀₀₀ = 0,125 .

Ma cosa succede se non hai con te la connessione d'Internet o una calcolatrice, ma solo carta e penna📝? E la tua frazione non è così facile da espandere come quelle precedenti? Allora probabilmente dovrai fare la divisione lunga con i decimali a mano. Buona fortuna! 🤞

Per poterlo fare è necessario trovare un denominatore comune. Utilizzeremo 1/2 e 3/5 come esempio. Segui questi passaggi per sommare frazioni con denominatori diversi:

1. Trova il minimo comune multiplo (m.c.m.) del denominatore:

   10 ;

2. Dividi l'm.c.m. per ciascun denominatore e moltiplica i numeratori per la risposta:

   • 10/2 = 5
     5 × 1 = 5 ,

   • 10/5 = 2
     2 × 3 = 6 ;

3. Aggiungi i numeri trovati al punto 2 e posiziona il risultato sopra l'm.c.m.:

   • 6 + 5 = 11

   • 11/10 = 1 ¹/₁₀ ; e

4. Voilà! Hai sommato le frazioni.

Sì, ogni frazione è un numero razionale, ma non tutti i numeri razionali sono frazioni. Un numero razionale è una frazione solo quando il numeratore e il denominatore sono numeri interi.

0,3333 scritto come frazione è ³³/_10 000 .

Per trovare questa risposta:

1. Scrivi il decimale come numeratore e 1 come denominatore:

   0,3333/1 ;

2. Sposta il punto decimale a destra alla fine del numero in modo che appaia come un integrale:

   3 333 ;

3. Aggiungi al denominatore lo stesso numero di zeri del numero di posizioni in cui hai spostato il punto decimale. In questo caso, sono quattro:

   10 000 ; e

4. Metti il numero del passo 2 al numeratore e il numero del passo 3 al denominatore:

   3 333/10 000 .

Il prodotto di 1/2 e 5/3 è 5/6.

Per arrivare a questa risposta, moltiplichiamo i numeratori e i denominatori nel seguente modo:

• 1 × 5 = 5; e

• 2 × 3 = 6; quindi

• 1/2 × 5/3 = 5/6.