Calcolatore per Angoli Orientati

Il nostro calcolatore per angoli orientati è un pratico strumento per calcolare gli angoli nella loro versione acuta. Tutto quello che devi fare è inserire nel campo un angolo positivo qualsiasi e il calcolatore troverà l'angolo orientato per te. Questo articolo spiega cos'è un angolo orientato e fornisce una definizione di angolo orientato.

Inoltre, ti fornirà una guida passo a passo su come trovare un angolo orientato in radianti e gradi, insieme ad alcuni esempi. Continuando a scorrere, troverai anche un grafico con i quadranti!

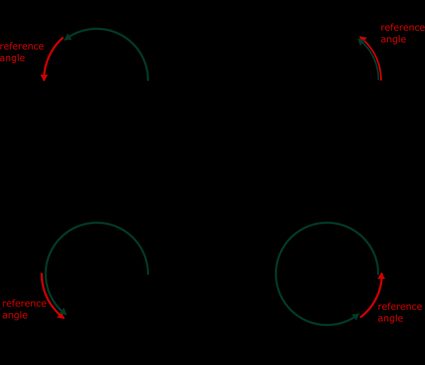
Guarda l'immagine qui sopra. Ogni angolo viene misurato dalla parte positiva dell'asse x alla sua linea di riferimento (la linea che determina la fine dell'angolo) in senso antiorario. Se vuoi trovare l'angolo orientato, devi trovare il più piccolo angolo possibile formato dall'asse x e dalla linea di riferimento, in senso orario o antiorario.

Gli angoli di riferimento sono utili in trigonometria. Se vuoi trovare il seno o il coseno di un angolo arbitrario, devi prima cercare il suo angolo orientato nel primo quarto. Poi puoi trovare la funzione trigonometrica dell'angolo orientato e scegliere il segno corretto.

Gli angoli più comunemente utilizzati e le loro funzioni trigonometriche sono riportati nella tabella seguente:

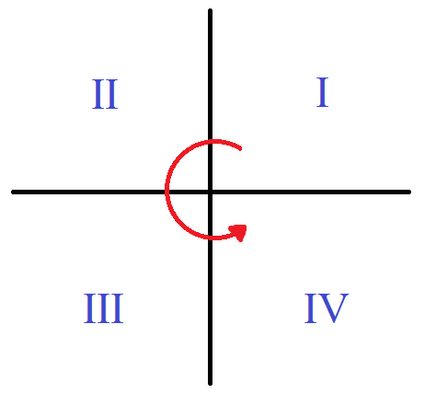
I due assi di un sistema cartesiano 2D dividono il piano in quattro regioni infinite chiamate quadranti. La numerazione parte dal quadrante superiore destro, dove entrambe le coordinate sono positive, e procede in senso antiorario, come nell'immagine.

In genere, le funzioni trigonometriche (seno, coseno, tangente, cotangente) forniscono lo stesso valore sia per un angolo che per il suo angolo orientato. L'unica cosa che cambia è il segno — queste funzioni sono positive e negative in diversi quadranti.
Per ricordare quando le funzioni sono positive, proponiamo l’esempio della regola ASTC (All Sine Tangent Cosine dall’inglese). Questa regola mnemonica recita "All Students Take Calculus" — vi proponiamo la versione italiana come TSTC o Tutti Sembrano Tanto Contenti:

• T per tutti — Nel primo quadrante, tutte le funzioni trigonometriche hanno valori positivi;
• S per seno — Nel secondo quadrante, solo la funzione seno ha valori positivi;
• T per tangente — Nel terzo quadrante, la tangente e la cotangente hanno valori positivi; e
• C per coseno — Nel quarto quadrante, solo la funzione coseno ha valori positivi.

Se questa regola non ti piace, ecco altre mnemotecniche da ricordare:

• Tutti Saltano sul Tetto e Cadono 🏡
• Tanti Signori Tornano a Casa 🚗
• Torte Salate per Tutta la Cucina 🍰

Assicurati di dare un'occhiata al calcolatore per il teorema del coseno e al calcolatore della legge dei seni per maggiori informazioni sulla trigonometria.

Tutto quello che devi fare è seguire questi passaggi:

1. Scegli il tuo angolo iniziale, ad esempio 610°.

2. Se il tuo angolo è più grande di 360° (un angolo intero), sottrai 360°. Continua a farlo finché non ottieni un angolo più piccolo di un angolo intero. Questo equivale a trovare il modulo. In questo esempio, dopo aver sottratto 360°, otteniamo 250°.

3. Determina in quale quadrante si trova il tuo angolo:

   • Da 0° a 90° — Primo quadrante,
   • Da 90° a 180° — Secondo quadrante,
   • Da 180° a 270° — Terzo quadrante,
   • Da 270° a 360° — Quarto quadrante.

   In questo caso, 250° si trova nel terzo quadrante.

4. Scegli la propria formula per calcolare l'angolo orientato:

   • Da 0° a 90° — Angolo orientato = angolo,
   • Da 90° a 180° — Angolo orientato = 180° − angolo,
   • Da 180° a 270° — Angolo orientato = angolo − 180°,
   • Da 270° a 360° — Angolo orientato = 360° − angolo.

   In questo caso, dobbiamo scegliere la formula: Angolo orientato = angolo − 180°.

5. Sostituisci il tuo angolo nell'equazione per trovare l'angolo orientato:

   Angolo orientato = 250° − 180° = 70°.

Se hai bisogno di uno strumento che ti aiuti a convertire le unità di misura degli angoli, prova il nostro convertitore di angoli 🇺🇸.

È più facile di quanto sembri!

1. Per angoli superiori a 2π, sottrai multipli di 2π fino a ottenere un valore inferiore all'angolo intero; e
2. Determina i quadranti:

• Da 0 a π/2 — Primo quadrante, quindi Angolo orientato = angolo;
• Da π/2 a π — Secondo quadrante, quindi Angolo orientato = π − angolo;
• Da π a 3π/2 — Terzo quadrante, quindi Angolo orientato = angolo − π; e
• Da 3π/2 a 2π — Quarto quadrante, quindi Angolo orientato = 2π − angolo.

Come puoi vedere, questa procedura è simile a quella descritta sopra per i gradi. Come esempio, consideriamo
l'angolo di 28π/9 radianti.

1. Avendo sottratto i multipli di 2π, ci rimane 10π/9; e

2. 10π/9 è un po' più di π, quindi si trova nel terzo quadrante. L'angolo orientato è:

   Angolo orientato = angolo - π = π/9.

Non potrebbe essere più facile! Semplicemente:

1. Digita l'angolo nel riquadro. Può essere un angolo positivo qualsiasi; diciamo che vogliamo trovare l'angolo orientato per 210°. Se lo desideri, puoi anche cambiare le unità di misura, ad esempio in radianti; ed
2. Ecco fatto! Questo calcolatore per angoli orientati ha trovato la versione acuta del tuo angolo e il quadrante in cui si trova l'angolo iniziale. Nel nostro caso è di 30° e l'angolo iniziale si trova nel terzo quadrante. Fantastico!

Se vuoi una risposta rapida, dai un'occhiata all'elenco seguente:

Primo quadrante:

Secondo quadrante:

Terzo quadrante:

Quarto quadrante: