Calcolatore per l'Angolo tra due Vettori

Con questo calcolatore per l'angolo tra due vettori, imparerai rapidamente a trovare l'angolo tra due vettori. Non importa se i tuoi vettori sono in 2D o 3D, né se le loro rappresentazioni sono coordinate o punti iniziali e terminali — il nostro strumento è una scommessa sicura in ogni caso. Esplora il calcolatore e controlla le definizioni e le spiegazioni qui sotto — se stai cercando le formule dell'angolo tra due vettori, sei nel posto giusto.

In questo paragrafo troverai le formule dell'angolo tra due vettori — e solo le formule. Se vuoi capire come le abbiamo ricavate, vai direttamente al paragrafo successivo, Come trovare l'angolo tra due vettori.

Angolo tra due vettori 2D

1. Vettori rappresentati da coordinate (notazione standard degli insiemi ordinati, forma componente):

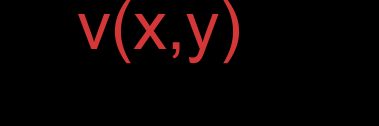
Per il vettore $\boldsymbol a$:

E $\boldsymbol b$:

L'angolo è:

2. Vettori tra un punto iniziale e uno finale:

Per il vettore $\boldsymbol a$:

E:

Perciò il vettore $\boldsymbol a$ è:

Per il vettore $\boldsymbol b$:

E:

Quindi il vettore $\boldsymbol b$ è:

E:

Angolo tra due vettori 3D

1. Vettori rappresentati da coordinate:

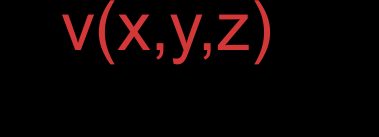
E:

Poi:

2. Vettori tra un punto iniziale e uno finale:

Per il vettore $\boldsymbol{a}$:

E:

Quindi:

Per il vettore $\boldsymbol{b}$:

E:

Perciò:

Trova la formula finale in modo analogo alla versione 2D:

Inoltre, è possibile che un vettore sia definito da coordinate e l'altro da un punto di partenza e un punto di arrivo, ma non lasceremo che ciò oscuri ulteriormente questa sezione. L'importante è che il nostro calcolatore per l'angolo tra due vettori ti metta a disposizione tutte le combinazioni possibili.

Ok, il paragrafo precedente era un po' un papiro. Per capire meglio le formule dell'angolo tra due vettori, verifichiamola loro origine:

1. Inizia con la formula geometrica di base per calcolare il prodotto scalare 🇺🇸:

   Il prodotto dei punti è definito come il prodotto delle grandezze dei vettori moltiplicato per il coseno dell'angolo tra di essi (qui indicato con $\alpha$):

2. Quindi, fai dell'angolo l'oggetto dell'equazione:

   Dividi per il prodotto delle grandezze dei vettori:

Trova il coseno inverso di entrambi i lati:

3. In seguito, dobbiamo ripassare la definizione della grandezza di un vettore:

   Dato che la magnitudine è la radice quadrata della somma delle componenti del vettore alla seconda potenza, scopriamo che:

   • $|\boldsymbol{v}| =\sqrt{x^2+y^2}$ nello spazio 2D; e

   • $|\boldsymbol{v}| =\sqrt{x^2+y^2+z^2}$ nello spazio 3D.

Hai notato che è la stessa formula utilizzata nel calcolatore per la distanza? E che deriva direttamente dalla geometria — vorresti impararla con il calcolatore per il teorema di Pitagora?

4. Usa la formula algebrica del prodotto di punti (la somma dei prodotti delle componenti dei vettori) e sostituisci le grandezze:

Nello spazio bidimensionale:

Se i vettori $\boldsymbol{a}$ e $\boldsymbol{b}$ sono rispettivamente:

E:

Nello spazio tridimensionale:

Se i vettori $\boldsymbol{a}$ e $\boldsymbol{b}$ sono rispettivamente:

E:

Dunque:

E questo è tutto!

Inoltre, se i tuoi vettori hanno una forma diversa (conosci i loro punti iniziali e terminali), dovrai eseguire alcuni calcoli in anticipo. L'obiettivo è quello di ridurli in notazione vettoriale standard.

Se il tuo vettore di esempio è descritto dal punto iniziale $A=(x_1, y_1)$ e dal punto terminale $B=(x_2, y_2)$, allora il vettore$\boldsymbol{a}$ può essere espresso come:

Non ha ancora senso? Non preoccuparti! Abbiamo preparato alcuni calcoli esemplari per assicurarci che sia chiaro come l'acqua.

Supponiamo di voler trovare l'angolo tra due vettori:

e $\boldsymbol{b}$ è definito come il vettore tra il punto $A = (1, 1, 2)$ e $B = (-4, -8, 6)$.

Cosa bisogna fare?

1. Per prima cosa, calcola il vettore $\boldsymbol{b}$ dati i punti iniziali e finali

2. Quindi, trova il prodotto di punti dei vettori $\boldsymbol{a}$ e $\boldsymbol{b}$:

3. Successivamente, determina la grandezza dei vettori:

E:

4. Infine, utilizza l'equazione del prodotto di punti trasformato:

Ed ecco fatto! Hai appena calcolato l'angolo tra due vettori 3D. Congratulazioni!

Se vuoi imparare altri concetti di geometria delle coordinate, ti consigliamo di consultare il calcolatore del tasso medio di variazione.

Quindi, come funziona il nostro calcolatore per l'angolo tra due vettori? Segui queste istruzioni passo dopo passo:

1. Scegli il tuo spazio vettoriale. Consideriamo lo stesso esempio del paragrafo precedente. I nostri vettori e punti hanno tre coordinate, quindi dobbiamo scegliere l'opzione 3D;

2. Scegli la rappresentazione del primo vettore. Il primo vettore è in notazione standard, quindi lasciamo il valore predefinito — rappresentazione delle coordinate;

3. Inserisci il primo vettore. Digita $x = 3,$ $y = 6,$ e $z = 1$;

4. Scegli la rappresentazione del secondo vettore. Questa volta dobbiamo cambiare in rappresentazione del punto;

5. Inserisci i valori del secondo vettore. Inserisci $\boldsymbol A = (1,1,2)$ e $\boldsymbol B = (-4,-8,6)$ nei campi appropriati; e

6. Lo strumento ha trovato l'angolo tra due vettori 3D nel momento in cui compili l'ultimo campo. Nel nostro caso, è $150,\!2\degree$ — che è, ovviamente, lo stesso risultato ottenuto con i calcoli manuali.

Un vettore è una componente geometrica che ha sia una grandezza sia una direzione. È molto comune utilizzarli per rappresentare quantità fisiche come la forza, la velocità e lo spostamento, tra le altre.

L'angolo formato tra due vettori è definito utilizzando il coseno inverso dei prodotti dei punti dei due vettori e il prodotto delle loro grandezze.

Per calcolare l'angolo tra due vettori in uno spazio 2D:

1. Trova il prodotto di punti dei vettori;
2. Dividi il prodotto del punto per la grandezza del primo vettore; e
3. Dividi la risultante per la grandezza del secondo vettore.

Matematicamente, l'angolo α tra due vettori [x_a, y_a] e [x_b, y_b] può essere scritto come:

α = arcocoseno[(x_a x_b + y_a y_b) / (√(x_a² + y_a²) × √(x_b² + y_b²))].

Per calcolare l'angolo tra due vettori in uno spazio 3D:

1. Trova il prodotto di punti dei vettori;
2. Dividi il prodotto del punto per la grandezza del primo vettore; e
3. Dividi la risultante per la grandezza del secondo vettore.

Matematicamente, l'angolo α tra due vettori [x_a, y_a, z_a] e [x_b, y_b, z_b] può essere scritto come:

α = arccos[(x_a x_b + y_a y_b + z_a z_b) / (√(x_a² + y_a² + z_a²) × √(x_b² + y_b² + z_b²)].