Calcolatore per l'Angolo di Elevazione

Questo calcolatore per l'angolo di elevazione determina ed esprime, in quattro modi diversi, la pendenza di una superficie in terra. Può essere indicata in termini di grado di elevazione rispetto al piano orizzontale, in termini di percentuale di deviazione dalla linea orizzontale o semplicemente in termini di rapporto "dislivello/lunghezza". Per calcolare la pendenza di una retta e per saperne di più sulle pendenze in generale, puoi consultare il nostro calcolatore del coefficiente angolare. Per saperne di più su come trovare la pendenza del terreno (o del terreno in generale), continua a leggere.

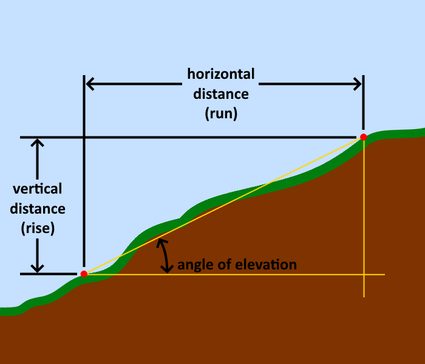
L'angolo di elevazione (o pendenza) è la ripidità, o il grado di inclinazione, di una certa area di terreno. Può essere semplicemente la pendenza tra due punti specifici di una determinata area, la media delle variazioni graduali di pendenza di un'area o una variazione irregolare dell'elevazione del terreno. Di solito misuriamo l'elevazione del terreno come la sua altitudine sul livello del mare. I geometri e gli ingegneri sono generalmente coloro che misurano e registrano queste quote utilizzando attrezzature e strumenti di rilevamento.

Conoscere il grado altimetrico di un'area offre molti vantaggi rispetto a non conoscerlo affatto. Può anche essere un requisito per procedere con altre attività, come la costruzione o l'irrigazione. Ecco alcuni esempi dell'importanza e dei vantaggi di conoscere l'altitudine di una determinata area:

• Conoscere il grado altimetrico dell'area aiuta nella costruzione di strade. La utilizziamo, ad esempio, nella formula della curva verticale 🇺🇸. Un terreno molto ripido può richiedere che le strade siano tracciate a zig-zag per rendere più sicure le salite e le discese. Gli ingegneri possono progettare una procedura di taglio e riempimento per i terreni meno ripidi per diminuire la pendenza. Il taglio e il riempimento consiste nel trasferire il terreno dalla parte più alta del pendio a quella più bassa per ridurne la pendenza;

• La determinazione della pendenza altimetrica è utile anche per la costruzione di muri di sostegno. I muri di sostegno sostengono la terra sovrastante per evitare che si eroda verso il basso. Per questo motivo un muro di contenimento può essere costruito contro una scogliera per evitare frane.
  Se vuoi saperne di più sui muri di contenimento, dai un'occhiata al nostro calcolatore per muri di sostegno;

• Anche conoscere l'angolo di elevazione del terreno è utile per valutare la capacità di un terreno di sostenere una struttura. La costruzione di strutture in un'area in pendenza potrebbe richiedere delle fondamenta aggiuntive per evitare di crollare;

• L'angolo di elevazione è utile anche per esaminare il flusso dell'acqua dalle altezze più elevate per verificare se il terreno può essere irrigato senza pompe; e

• Molte altre cose. :)

Calcoliamo la pendenza del terreno nello stesso modo in cui calcoliamo la pendenza di una linea. La pendenza di una determinata linea richiede le coordinate dei suoi punti finali. La pendenza è il quoziente della variazione dei valori di y e della variazione dei valori di x. Come equazione, si presenta così:

Nella comunità matematica, questi cambiamenti nei valori di x e y hanno dei soprannomi. Chiamiamo la variazione dei valori di y "dislivello", poiché si sviluppa lungo l'asse verticale. D'altro canto, chiamiamo la variazione dei valori di x "lunghezza", poiché si sviluppa lungo l'asse orizzontale. Questa relazione ci dà la famosa equazione che potresti aver già sentito: "La pendenza è uguale al rapporto dislivello/lunghezza" Oppure:

Oltre a questo, possiamo anche esprimere il grado in termini di angoli. Per ottenere l'angolo abbiamo bisogno dell'aiuto della trigonometria. A noi interessa ottenere l'angolo tra il piano orizzontale e il piano di inclinazione. Un angolo che sale rispetto alla linea orizzontale viene chiamato "angolo di elevazione", mentre quelli che scendono sono l'"angolo di declinazione" Possiamo determinare questo angolo utilizzando la funzione arctan. La funzione arctan è l'inverso della funzione tangente con la pendenza come argomento. In forma di equazione, si presenta come segue:

Se non hai un calcolatore con questa funzione trigonometrica, non preoccuparti, l'abbiamo già incorporata nel nostro calcolatore per l'angolo di elevazione qui sopra. Se vuoi saperne di più sulle altre funzioni trigonometriche essenziali, puoi consultare il nostro calcolatore delle funzioni trigonometriche 🇺🇸 e giocare con gli angoli.

Oltre a esprimere il grado utilizzando rapporti e angoli, possiamo anche determinarlo in termini di percentuali — basta moltiplicare il valore del rapporto per 100 per ottenerlo. È da qui che nasce l'equazione qui sotto. Una pendenza del cento per cento significa che la salita del pendio è uguale alla sua discesa. La pendenza risultante per questo valore non è considerata né ripida né piatta, ma piuttosto una pendenza media. Ecco la forma dell'equazione:

Abbiamo dotato il nostro calcolatore per l'angolo di elevazione di tutte queste equazioni, in modo che possa darti tutte le risposte di cui hai bisogno ogni volta che inserisci un valore per una qualsiasi variabile. Puoi impostare la pendenza e determinare la distanza orizzontale necessaria per ottenere la variazione richiesta in una distanza verticale, oltre a ottenere l'angolo di elevazione.

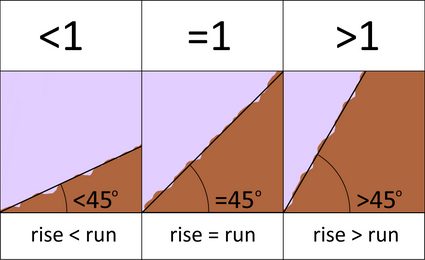
I valori dei gradi sono piuttosto facili da capire. I gradi del terreno inferiori a 1 (grado del terreno <1) vuol dire che la pendenza è piatta. D'altro canto, i gradi del terreno superiori a uno (grado del terreno >1) indicano che il terreno è ripido. In termini di angolo di elevazione, gli angoli superiori a 45 gradi sono quelli ripidi, mentre quelli inferiori a 45 gradi sono relativamente piatti.

Possiamo ottenere la "lunghezza", ovvero la variazione della distanza orizzontale, utilizzando un nastro di misurazione. Dovremo tirare il nastro per ottenere una misura precisa. Tuttavia, se non lo tiriamo, il valore sarà più alto di quello reale perché il nastro si affloscia a causa della gravità.

D'altra parte, possiamo ottenere la distanza verticale utilizzando dispositivi ottici, come un transito da geometra abbinato a una asta di livellamento. Un telescopio da geometra ha un telescopio incorporato che può essere ruotato lateralmente o verticalmente su un treppiede. Mettendo a fuoco l'asta di livellamento (che è come un enorme righello) si ottiene una lettura. Possiamo tradurre questa lettura nell'elevazione tra l'asta di livellamento e il transito. Il transito per geometri ha anche dei segni distintivi sulla visuale che lo rendono in grado di misurare anche le distanze orizzontali se abbinato a un'asta di livellamento.

Possiamo anche utilizzare uno strumento come il clinometro, che può fornire direttamente l'angolo di elevazione tra due punti. Un clinometro è come un mini telescopio con un goniometro attaccato al lato. Altri gadget digitali più sofisticati possono ora aiutare a ottenere la pendenza di una particolare superficie. Uno smartphone, se dotato di hardware adeguato come i sensori giroscopici, può fornirti con precisione la pendenza di una superficie quando lo appoggi sul pendio.

Possiamo tracciare le medie dei gradi del terreno per comporre una mappa delle curve di livello. Una mappa delle curve di livello è una mappa topografica che offre agli spettatori una panoramica del terreno di una determinata area. L'esagerazione verticale è spesso necessaria per enfatizzare alcune caratteristiche del terreno, come l'altezza delle montagne o dei vulcani.

Per saperne di più sull'esagerazione verticale, consulta il nostro calcolatore per l'esagerazione verticale 🇺🇸.

Baldwin Street, in Nuova Zelanda, ha una pendenza impressionante di circa 0,35, che corrisponde a una lunghezza orizzontale di 2,86 m per ogni metro verticale. La strada, lunga 350 metri, è una vera sfida da percorrere a piedi!

Una pendenza di 0,35 corrisponde a un angolo di:
Angolo = arctan(dislivello/lunghezza) = arctan(1/2,86) = 19,27°.

La formula fornisce la pendenza definita come un angolo:
Pendenza (angolo) = arctan(dislivello/lunghezza).
Dove il dislivello è la distanza verticale e la lunghezza è la distanza orizzontale di un pendio.
Per calcolare la pendenza in percentuale, prendi l'argomento della funzione arcotangente e moltiplicalo per 100:
Pendenza (percentuale) = dislivello/lunghezza × 100.

In modo piuttosto controintuitivo, una pendenza del 100% corrisponde a un angolo di 45°. Tuttavia, considera che la pendenza è il risultato dell'equazione:
Pendenza = dislivello/lunghezza,
dove

• Dislivello — Distanza verticale; e
• Lunghezza — Distanza orizzontale.

Un pendio in cui ogni metro orizzontale corrisponde a un metro verticale ha una pendenza di 1, che moltiplicata per 100 dà il valore 100%.

Supponiamo che la strada abbia una salita di 12 metri per ogni 200 metri di percorso. La pendenza sarebbe di 0,06. Per calcolare la pendenza di una strada con:

• Dislivello = 12 m; e
• Lunghezza = 200 m.

1. Calcola il rapporto tra salita e discesa:
   Grado = dislivello/lunghezza = 12/200 = 0,06;

2. Se vuoi conoscere l'angolo della pendenza, inserisci il valore nella funzione arcotangente:
   Pendenza (angolo) = arctan(dislivello/lunghezza) = arctan(12/200) = 3,43°; e

3. Se vuoi conoscere la pendenza in percentuale, moltiplica il rapporto per 100:
   Pendenza (percentuale) = 100 × dislivello/lunghezza = 6%.