Calculateur d'intervalle de confiance

Ce calculateur d'intervalle de confiance est un outil qui vous aidera à trouver l'intervalle de confiance pour un échantillon donné. Pour cela, vous devez entrer la moyenne 🇺🇸, l'écart-type et la taille de l'échantillon. Vous pouvez l'utiliser pour n'importe quel niveau de confiance. Si vous voulez savoir ce qu'est exactement l'intervalle de confiance et comment le calculer, ou si vous cherchez la formule de l'intervalle de confiance à 95 % pour le score Z, cet article va certainement vous aider.

Un intervalle de confiance est défini comme « la plage de valeurs, dérivée des données d'un échantillon, qui est susceptible de contenir la valeur d'un paramètre de population inconnu. » Mais qu'est-ce que cela signifie en réalité ?

Imaginez qu'un fabricant de briques se demande si la masse des briques qu'il fabrique est conforme aux réglementations. Il a estimé la masse moyenne d'un échantillon de 100 briques à environ 3 kg. Il a également constaté que l'intervalle de confiance à 95 % était compris entre 2,85 kg et 3,15 kg. Cela signifie qu'il peut être sûr à 95 % que la masse moyenne de toutes les briques qu'il fabrique sera comprise entre 2,85 kg et 3,15 kg. Plus précisément : si le fabricant de briques a collecté un grand nombre d'échantillons de 100 briques et a utilisé chaque échantillon pour calculer l'intervalle de confiance, alors 95 % de ces intervalles contiendront la véritable masse moyenne d'une brique.

Bien sûr, vous ne voulez pas toujours être sûr∙e à 95 %. Si vous avez besoin d'être très sûr∙e de votre estimation, vous choisirez un niveau de confiance élevé, comme 99 %. Si vous pouvez vous contenter d'une approximation, vous choisirez un niveau de confiance plus faible, comme 90 %. Ce pourcentage est appelé niveau de confiance.

Le calcul de l'intervalle de confiance nécessite de connaître trois paramètres de votre échantillon : la valeur moyenne, μ, l'écart-type, σ, et la taille de l'échantillon, n (nombre de mesures effectuées). Vous pouvez ensuite calculer l'erreur type 🇺🇸 puis la marge d'erreur selon les formules suivantes :

erreur type = σ/√n

marge d'erreur = erreur type × Z(0,95)

Où Z(0,95) est le score Z correspondant au niveau de confiance de 95 %. Si vous utilisez un niveau de confiance différent, vous devez calculer le score Z approprié à la place de cette valeur. Mais ne vous inquiétez pas, notre calculateur de score Z vous facilitera la tâche !

Comment trouver la valeur Z(0,95) ? Il s'agit de la valeur du score Z lorsque le niveau de confiance bilatéral est égal à 95 %. Cela signifie que si vous dessinez une courbe de loi normale 🇺🇸, la zone entre les deux scores Z sera égale à 0,95 (sur 1).

Si vous souhaitez calculer cette valeur à l'aide d'un tableau de scores Z, voici ce que vous devez faire :

1. Déterminez votre niveau de confiance. Supposons qu'il soit de 95 %.
2. Calculez la probabilité que votre résultat ne soit pas dans l'intervalle de confiance. Cette valeur est égale à 100 % - 95 % = 5 %.
3. Examinez la courbe de la loi normale. L'aire située au milieu correspond au 95 %. Cela signifie que l'aire à gauche de votre score Z est égale à 0,025 (2,5 %) et que l'aire à droite de votre score Z est également égale à 0,025 (2,5 %).
4. L'aire à droite de votre score Z est exactement la même que la valeur p de votre score Z. Vous pouvez utiliser les tableaux de scores Z pour trouver le score Z correspondant à une valeur p de 0,025. Dans ce cas, il est de 1,959.

Une fois que vous avez calculé la valeur Z(0,95), il vous suffit de saisir cette valeur dans l'équation ci-dessus pour obtenir la marge d'erreur. Il ne vous reste plus qu'à trouver les bornes inférieure et supérieure de l'intervalle de confiance :

borne inférieure = moyenne - marge d'erreur

borne supérieure = moyenne + marge d'erreur

Pour calculer un intervalle de confiance (bilatéral), suivez ces étapes :

1. Supposons que la taille de l'échantillon soit de 100.
2. Trouvez la valeur moyenne de votre échantillon. Supposons qu'elle soit de 3.
3. Déterminez l'écart-type de l'échantillon. Supposons qu'il soit de 0,5.
4. Choisissez le niveau de confiance. Le niveau de confiance le plus courant est : 95 %.
5. Dans le tableau de scores Z, trouvez le score Z(0,95), c'est-à-dire le 97,5ᵉ quantile de N(0,1) – dans notre cas, il est de 1,959.
6. Calculez l'erreur type tel que σ/√n = 0,5/√100 = 0,05.
7. Multipliez cette valeur par le score Z pour obtenir la marge d'erreur : 0,05 × 1,959 = 0,098.
8. Ajoutez et soustrayez la marge d'erreur de la valeur moyenne pour obtenir l'intervalle de confiance. Dans notre cas, l'intervalle de confiance est compris entre 2,902 et 3,098.

Et voilà ! Cela fait beaucoup de calculs, n'est-ce pas ? Heureusement, notre calculateur d'intervalle de confiance effectue tous ces calculs à votre place.

L'intervalle de confiance peut aussi être utilisé dans l'analyse des séries temporelles. L'échantillon de données représente alors une suite d'observations dans un laps de temps spécifique.

Un sujet fréquent de ce type d'étude est de savoir si un changement dans une variable a une incidence sur une autre variable en particulier.

Pour être plus précis, prenons l'exemple d'une question qui intéresse souvent les économistes : « Comment une variation du taux d'intérêt affecte-t-elle le niveau des prix ? »

Cette question est complexe et nécessite une analyse théorique et empirique approfondie. Cette analyse dépasse largement le cadre de ce texte. Mais il existe en effet de nombreuses techniques pour estimer et appliquer les intervalles de confiance. Cet exemple permet simplement de comprendre comment un intervalle de confiance peut être utilisé pour répondre à une question complexe.

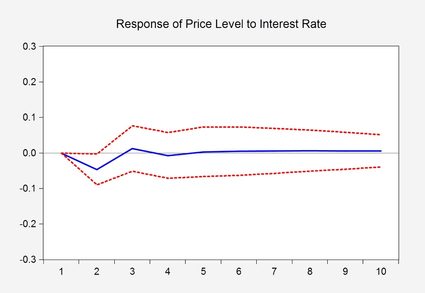
Le graphique ci-dessus est une représentation visuelle de la fonction de réponse aux impulsions d'un modèle économétrique. Cette fonction montre comment une variable économique, dans ce cas le niveau des prix, réagit à un changement d'une autre variable, ici le taux d'intérêt. La ligne bleue représente la réponse estimée, tandis que les lignes rouges en pointillés représentent un intervalle de confiance à 95 %. Cet intervalle indique que, avec une probabilité de 95 %, la réponse réelle se situe entre les lignes rouges. Plus précisément, le graphique montre que le niveau des prix ne commence à augmenter que deux mois après un changement du taux d'intérêt.

En résumé, nous espérons que les exemples ci-dessus et leur brève description vous permettront de mieux comprendre l'objectif de l'intervalle de confiance et vous inciteront à utiliser notre calculateur d'intervalles de confiance.

Si vous prenez plusieurs échantillons d'une population, la véritable moyenne de la population sera contenue dans environ 95 % des intervalles de confiance si vous choisissez un niveau de confiance de 95 %. Les 5 % d'intervalles restants ne contiendront pas la vraie moyenne de la population.

Le score Z pour un intervalle de confiance bilatéral à 95 % est 1,959, ce qui correspond au 97,5ᵉ quantile de la loi normale centrée réduite N(0,1).

Le score Z pour un intervalle de confiance bilatéral de 99 % est 2,807, ce qui correspond au 99,5ᵉ quantile de la loi normale centrée réduite N(0,1).

La taille d'un intervalle de confiance augmente lorsque la marge d'erreur augmente, ce qui se produit lorsque :

• le seuil de signification augmente ;
• la taille de l'échantillon diminue ; ou
• la variance de l'échantillon augmente.

La taille d'un intervalle de confiance diminue lorsque la marge d'erreur diminue, ce qui se produit lorsque :

• le seuil de signification diminue ;
• la taille de l'échantillon augmente ; ou
• la variance de l'échantillon diminue.

La moyenne de l'échantillon n'a aucun impact sur la taille d'un intervalle de confiance !