Avec ce calculateur de périmètre, vous n'avez plus à vous soucier des calculs de périmètre. Vous trouverez ci-dessous les formules de calcul du périmètre de douze formes géométriques différentes, ainsi qu'un bref rappel de la définition du périmètre.
Dans cet article, vous découvrirez :
- comment calculer un périmètre ;
- quelle est la formule du périmètre d'un rectangle ;
- comment calculer le périmètre d'un carré ;
- comment calculer le périmètre d'un cercle ; et
- bien d'autres formules et astuces !
Poursuivez votre lecture, essayez-le ou consultez notre calculateur d'aire pour approfondir vos connaissances en géométrie. Ne vous arrêtez pas à la fin de l'article ! Dans la section FAQ, vous trouverez des réponses à d'autres questions importantes, telles que « Comment calculer le périmètre d'une figure quelconque ? » et « C'est quoi le périmètre d'un cercle ? ».
À la fin de la lecture, vous saurez comment calculer le périmètre d'un triangle quelconque et comment trouver le périmètre d'un cercle en cm2, entre autres. Alors, qu'attendez-vous ?
Qu'est-ce que le périmètre ?
Le périmètre est la limite d'une figure géométrique fermée. Il peut également être défini comme le bord extérieur d'une aire, ou simplement comme la plus longue ligne continue qui entoure une forme. Le nom lui-même vient du grec perimetros : peri signifie « autour » et metron veut dire « mesure ». Comme il s'agit de la longueur du contour de la forme, elle est exprimée en unités de distance ; par exemple, en mètres, en pieds, en pouces ou en miles.
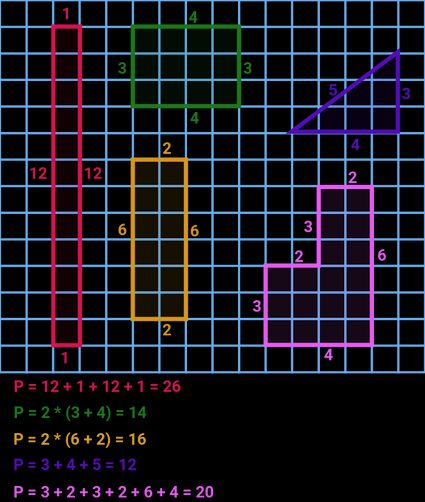
Calculateur de périmètre : comment calculer un périmètre ?
En général, l'approche la plus simple et la plus directe consiste à trouver la somme de tous les côtés d'une forme. Cependant, il existe des cas où il n'y a pas de côtés (comme une ellipse, un cercle, etc.), ou bien, un ou plusieurs côtés sont inconnus. Dans ce paragraphe, nous allons énumérer toutes les équations utilisées dans ce calculateur de périmètre.
Faites défiler les sections suivantes si vous êtes curieux ou curieuse d'en apprendre plus sur une forme géométrique spécifique et souhaitez avoir une explication, une démonstration et une image pour chacune des douze formes présentes dans ce calculateur. Nous avons également des outils dédiés à chaque forme : il vous suffit de taper le nom de la forme dans la barre de recherche en haut de cette page.
Voici les formules de calcul du périmètre pour les douze formes géométriques présentes dans ce calculateur :
-
Périmètre du carré :
-
Périmètre du rectangle :
-
Périmètre du triangle :
ou
ou
-
Périmètre du cercle :
-
Périmètre du secteur d'un cercle :
– en radians -
Périmètre de l'ellipse :
-
Périmètre d'un quadrilatère (ex. un trapèze) :
-
Périmètre du parallélogramme :
ou
ou
-
Périmètre du losange :
ou
-
Périmètre du cerf-volant :
-
Périmètre de la couronne :
-
Périmètre d'un polygone régulier :
Maintenant que vous savez comment calculer un périmètre en général, voyons toutes les formules plus en détail.
Formule du périmètre d'un carré

Vous vous demandez comment calculer le périmètre d'un carré ? C'est un jeu d'enfant, croyez-nous !
Un carré a quatre côtés de même longueur. Pour calculer son périmètre, il suffit de multiplier la longueur des côtés par :
Croyez-le ou non, mais nous avons aussi un calculateur de périmètre d'un carré 🇺🇸 !
Qu'en est-il du périmètre d'un rectangle ? Un carré n'est-il pas un rectangle particulier ?
Oui, mais le calcul du périmètre d'un rectangle est un tout petit peu plus compliqué que cela. Procédez pour le découvrir !
Formule du périmètre d'un rectangle

La formule du périmètre d'un rectangle est presque aussi simple que la formule du périmètre d'un carré. La seule différence est que nous avons deux paires de côtés de longueur égale. Voici l'équation qu'il vous faut pour effectuer le calcul du périmètre d'un rectangle :
Formule du périmètre d'un triangle

La formule la plus simple pour calculer le périmètre d'un triangle 🇺🇸 consiste, comme d'habitude , à additionner tous les côtés :

Cette formule suffit pour calculer le périmètre d'un triangle quelconque étant donné les côtés.
Cependant, vous ne connaissez pas toujours les trois côtés. Que faire alors ? Au lieu de vous énerver, vous pouvez utiliser le calculateur de la loi des cosinus 🇺🇸 pour trouver le côté manquant :
Ceci peut être utilisé dans la formule du périmètre :

L'autre possibilité consiste à utiliser la loi des sinus si vous disposez d'un côté et des deux angles adjacents à ce côté :
Et :
Le périmètre du triangle peut donc être exprimé comme suit :
Formule du périmètre d'un cercle : comment calculer le périmètre d'un cercle ?

Le périmètre d'un cercle porte un nom particulier : la circonférence.
« Comment calculer le périmètre d'un cercle ? », vous demandez-vous ? La formule du périmètre du cercle n'utilise qu'une seule variable, le rayon du cercle :
Si vous voulez calculer le périmètre d'un cercle en cm2, vous n'avez qu'à ajouter l'unité au rayon, ou le convertir, si besoin. Vous obtiendrez votre résultat en centimètres carrés !
Vous êtes-vous déjà demandé combien de fois la roue de votre vélo tourne-t-elle sur un trajet de 10 km ? C'est l'un des cas où vous devrez utiliser la formule de la circonférence. Entrez le rayon de votre roue (la moitié du diamètre de la roue), et divisez 10 km par la circonférence obtenue (mais n'oubliez pas la conversion des unités de longueur !). Si vous voulez être encore plus précis·e, vous pouvez inclure la taille du pneu du vélo.
Formule du périmètre d'un secteur de cercle

Le calcul du périmètre d'un secteur d'un cercle peut sembler délicat : s'agit-il uniquement de la longueur de l'arc, ou de la longueur de l'arc plus deux rayons ? Gardez à l'esprit la définition du périmètre ! Le périmètre d'un secteur est la somme des longueurs de toutes ses limites :
où :
– exprimé en radians
Formule du périmètre d'une ellipse (formule de la circonférence d'une ellipse)

On penserait que l'équation du périmètre d'une ellipse soit similaire à la formule du périmètre du cercle, mais ce n'est pas le cas.
Bien que la formule de l'aire d'une ellipse soit vraiment simple et facile à retenir, la formule du périmètre d'une ellipse est la plus difficile de toutes les équations énumérées ici. Nous avons choisi d'utiliser l'une des approximations de Ramanujan dans ce calculateur de périmètre :
où :
– le demi-petit axe (le rayon le plus court possible)
– le demi-grand axe (le rayon le plus long possible)
L'autre approximation de Ramanujan, plus précise, est la suivante :
Il existe également une forme plus simple, utilisant une variable supplémentaire :
C'est-à-dire :
Vous pouvez aussi utiliser notre calculateur !
Formule du périmètre d'un trapèze

Pour calculer le périmètre d'un trapèze irrégulier, il n'y a pas de formule particulière : il suffit d'additionner les quatre côtés :
Vous l'avez peut-être remarqué, mais c'est la formule pour le périmètre de tous les quadrilatères.
Certaines formes spécifiques de trapèzes peuvent être traitées différemment : comme le trapèze isocèle, pour lequel vous avez besoin de , , et côtés. Un autre exemple est le trapèze droit, pour lequel la longueur des bases et d'un côté est suffisante pour trouver le périmètre de la forme (pour trouver le dernier côté, nous utilisons le théorème de Pythagore).
Formule du périmètre d'un parallélogramme

Dans ce calculateur de périmètre, vous trouverez trois formules pour calculer le périmètre d'un parallélogramme :
- La plus simple, qui consiste à additionner tous les côtés :

- La formule du périmètre d'un parallélogramme qui utilise un côté et des diagonales.

- Le périmètre est donné en fonction de la base, la hauteur et tout angle du parallélogramme.
Formule du périmètre d'un losange

La formule du périmètre d'un losange n'a rien de sorcier. Savez-vous comment calculer le périmètre d'un carré ? Très bien ! La formule du périmètre d'un losange est exactement la même.

La méthode avec la formule du périmètre d'un carré est la plus simple, mais une autre solution pour trouver le périmètre du losange est d'utiliser les longueurs des diagonales :
Essayez de décomposer la formule vous-même. Vous savez que les deux diagonales d'un losange sont perpendiculaires et se coupent l'une l'autre, de sorte que vous pouvez diviser la forme en quatre triangles rectangles congruents. Chaque triangle a des côtés adjacents de longueur e/2 et f/2. Il vous suffit de trouver l'hypoténuse du triangle, qui est en même temps le côté du losange. Multipliez ensuite le résultat par quatre pour trouver la formule finale.
Formule du périmètre d'un cerf-volant

La formule pour calculer le périmètre d'un cerf-volant est assez simple ; il suffit d'additionner tous les côtés :
Formule du périmètre d'une couronne

Le périmètre étant défini comme la limite, pour calculer le périmètre d'une couronne, vous devrez effectuer le calcul du périmètre d'un cercle deux fois, en utilisant les rayons des deux cercles concentriques :
Formule du périmètre d'un polygone (pentagone régulier, hexagone, octogone, etc.)

Dans notre calculateur de périmètre, nous utilisons aussi une formule simple pour calculer le périmètre d'un polygone régulier :
où :
– le nombre de côtés du polygone
Ainsi, vous pouvez calculer le périmètre d'un pentagone, d'un hexagone, d'un octogone, etc.
En outre, pour les polygones jusqu'à 12 côtés, le nom du polygone apparaît dans l'outil. Génial, n'est-ce pas ?
Si vous souhaitez déterminer le périmètre de n'importe quel polygone, additionnez les longueurs de tous ses côtés :
où :
, , ..., – les longueurs des côtés
– le symbole de la somme (de à )
Vous pouvez également utiliser les coordonnées des sommets :
Avec et .
Nous espérons que notre article vous a plu et que vous savez maintenant comment calculer un périmètre. Voulez-vous en savoir plus ? Lisez la section FAQ ci-dessous !
FAQ
Comment calculer le périmètre d'une figure ?
Si vous voulez découvrir comment calculer le périmètre d'une figure quelconque, suivez ces étapes :
- Mesurez la longueur de tous les côtés extérieurs.
- Si les côtés comprennent des fragments circulaires, mesurez le rayon et l'angle au centre, c'est-à-dire l'angle entre les rayons qui joignent les deux extrémités de l'arc au centre.
- Utilisez la formule de calcul du périmètre d'un cercle avec le rayon donné et prenez la partie proportionnelle à l'angle. C'est le périmètre de l'élément arrondi de la figure.
- Additionnez les longueurs de tous les côtés et des parties arrondies.
C'est quoi le périmètre d'un cercle ?
Le périmètre d'un cercle n'est rien d'autre que sa circonférence. La formule de calcul du périmètre d'un cercle est désormais très connue :
périmètre = 2πr = πd
où :
r– rayon du cercled– diamètre du cercle
Quel est le périmètre d'un bâtiment rectangulaire de 20 m sur 15 m ?
Le périmètre est de 70 m. Pour arriver à ce résultat, il faut additionner les longueurs des quatre côtés du bâtiment. En d'autres termes, vous devez effectuer le calcul du périmètre d'un rectangle. Deux côtés de 20 m de long additionnés donnent 40 m, tandis que les deux autres côtés de 15 m de long additionnés donnent 30 m. Ensemble, nous obtenons 40 m + 30 m = 70 m, comme indiqué.