Calculateur de coefficient directeur

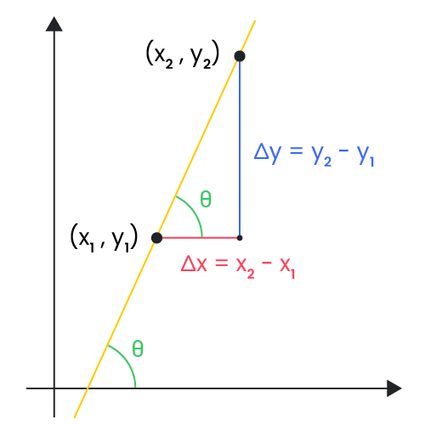
Ce calculateur détermine le coefficient directeur ou le gradient entre deux points dans un système de coordonnées cartésiennes. Ce coefficient directeur correspond à l'inclinaison d'une droite et peut avoir une valeur positive, négative, nulle ou indéfinie. Avant d'utiliser le calculateur, nous verrons comment déterminer le coefficient directeur à l'aide de la formule de ce dernier. Pour trouver l'équation d'une droite passant par deux points connus, utilisez notre calculateur de fonction affine.

Si les coordonnées sont de petits nombres entiers, il est assez facile de calculer le coefficient directeur (a) d'une droite à la main. La formule devient de plus en plus utile dès lors que les coordonnées prennent des valeurs plus grandes ou des valeurs décimales.

Il est important de souligner que toute droite horizontale a une pente nulle, car les coordonnées y sont les mêmes pour toutes les abscisses. Cela se traduit par un coefficient nul dans le numérateur de la formule du coefficient directeur.

En revanche, une ligne verticale aura un coefficient indéfini, parce que les coordonnées de x restent constants. Il en résultera une erreur de division par zéro.

1. Identifiez les coordonnées $(x_1,\ y_1)$ et $(x_2,\ y_2)$. Nous allons utiliser la formule pour calculer le coefficient directeur de la droite passant par les points $(3,\ 8)$ et $(-2,\ 10)$.

2. Entrez les valeurs dans la formule. On obtient $(10 - 8)/(-2 - 3)$.

3. Soustrayez les valeurs entre parenthèses pour obtenir $2/(-5)$.

4. Simplifiez la fraction pour obtenir un coefficient de $-2/5$.

5. Vérifiez votre résultat à l'aide du calculateur du coefficient directeur.

Pour trouver le coefficient directeur d'une droite, nous avons besoin de deux coordonnées quelconques de cette droite. Essentiellement, ce que l'on détermine c’est la variation de la coordonnée de y, divisée par la variation de l’abscisse x. Les calculs pour trouver le coefficient directeur sont simples et n'impliquent rien de plus qu'une soustraction et une division de base.

Tout comme on peut calculer le coefficient directeur à l’aide des extrémités d'un segment, on peut aussi calculer le point médian d’une droite.

Le point médian est un concept important en géométrie, notamment lorsqu'on inscrit un polygone de manière que les sommets du polygone inscrit touchent les points médians des côtés de l’autre. Vous pouvez trouver le point médian à l'aide du calculateur de point médian, ou tout simplement en prenant la moyenne de chaque coordonnée x et y pour former un nouveau couple de coordonnées.

Les coefficients directeurs des droites sont importants pour déterminer si un triangle est rectangle ou non. Si la multiplication des coefficients de deux côtés quelconques d’un triangle donne -1, alors ce triangle est rectangle.

Les calculs peuvent être effectués à la main ou à l'aide du calculateur de triangle rectangle. Vous pouvez également utiliser le calculateur de distance pour trouver quel côté d'un triangle est le plus long et pour déterminer quels côtés forment un angle droit, si le triangle est rectangle.

Le signe du coefficient directeur calculé par le calculateur de coefficient directeur indique si la fonction linéaire est croissante, décroissante, constante ou indéfinie. La droite est croissante si la fonction linéaire monte d’en bas à gauche vers le haut à droite. Son coefficient est donc positif. Si au contraire, la droite descend du haut à gauche vers le bas à droite, elle sera décroissante et alors, son coefficient sera négatif.

La méthode pour trouver le coefficient directeur à partir d'une équation varie en fonction de la forme de l'équation que vous avez devant vous. Si la forme de l'équation est y = mx + c, alors le coefficient directeur (ou le gradient) est simplement m. Si l'équation n'est pas sous cette forme, essayez de la réarranger. Pour déterminer le coefficient directeur d'autres polynômes, vous pouvez dériver votre fonction par rapport à x.

La pente d’une colline n’est rien d’autre que le coefficient directeur d’une droite dans la vie réelle. Pour déterminer la pente d'une colline, il vous faut suivre quelques étapes afin d'arriver à ce calcul.

1. Utilisez une carte géographique pour déterminer la distance entre le haut et le bas de la colline à vol d'oiseau.
2. À l'aide de la même carte ou d'un GPS, déterminez la hauteur de la colline. Assurez-vous que les points de mesure sont les mêmes qu'à l'étape 1.
3. Convertissez les deux mesures dans les mêmes unités.
4. Divisez la hauteur par la distance mesurée sur la carte.
5. Ce nombre correspond au coefficient directeur de la colline si son bord est linéaire. Si ce n'est pas le cas, répétez les étapes, mais à l'endroit où il y a un changement notable de coefficient directeur.

1. Mesurez la différence entre le haut et le bas de la droite par rapport à l'axe des x et y.
2. Si vous ne trouvez pas de variation dans l’axe des x, multipliez cette valeur par le coefficient directeur pour trouver la variation sur l'axe des y.
3. Assurez-vous que les unités des deux valeurs sont les mêmes.
4. Utilisez le théorème de Pythagore pour trouver la longueur de la droite. Élevez au carré la variation de x et y.
5. Additionnez les deux valeurs.
6. Trouvez la racine carrée de la somme.
7. Cette nouvelle valeur sera la longueur de votre droite.

Un coefficient directeur de 1/20 veut dire que pour chaque augmentation d'une unité sur l'axe des y, la droite va augmenter de 20 unités horizontalement.

Ainsi, par exemple, une rampe de 200 mètres de long et de 10 mètres de haut aurait une pente de 1/20. Un coefficient directeur de 1/20 équivaut à une inclinaison de 1/20 (curieusement) et forme un angle de 2,86° entre elle-même et l'axe des x.

Puisque le coefficient directeur d'une courbe change à chaque point, vous pouvez prendre la dérivée de l'équation par rapport à x et remplacer x par le point dont vous souhaitez trouver le coefficient directeur dans l'équation résultante.

Le taux de variation d'un graphique correspond également à la valeur de son coefficient directeur. Le taux de variation peut être obtenu en divisant la variation dans la direction y (verticale) par la variation dans la direction x (horizontale), si les deux nombres sont exprimés avec les mêmes unités, bien entendu.
Le taux de variation est particulièrement utile si vous voulez prédire l'avenir d’une valeur précédant une autre, car en changeant la variable x, la valeur y correspondante sera présente (et vice versa).

Les coefficients directeurs ont de nombreuses utilisations au quotidien.

Il existe des exemples physiques évidents :

• Toute colline a une pente et plus la colline est raide, plus sa pente aura une valeur importante.
• Cela peut être aussi utile si vous regardez une carte et que vous voulez trouver la meilleure colline à descendre à vélo.
• Vous dormez probablement même sous un coefficient directeur, c'est-à-dire sous un toit. Bien que la pente d'un toit varie en fonction du style et de l'endroit où vous vivez.
• Mais surtout, si vous voulez savoir comment quelque chose varie avec le temps, vous finirez par tracer une droite et son coefficient directeur.

Une pente de 10 % correspond à une droite qui s'élève d'une unité pour chaque 10 unités parcourues horizontalement (10 %). Par exemple, un toit de 20 m de large ayant une pente de 10 % aura une hauteur de 2 m. Cela correspond à un coefficient directeur de 1/10, et un angle de 5,71° sera formé entre la droite et l'axe des x.

Pour trouver l'aire sous une droite d'équation y = mx + c, suivez ces étapes :

1. Définissez les bornes inférieures et supérieures de x pour obtenir une valeur pour Δx.
2. Multipliez Δx par le coefficient directeur (m) pour obtenir Δy.
3. Multipliez Δx par Δy.
4. Divisez le résultat par 2 pour obtenir l'aire sous la droite.

Une droite de 5 pour 1 contient un coefficient directeur qui, pour chaque augmentation de 5 unités horizontales, s'élèvera de 1 unité. Une telle droite fera 11,3° par rapport à l'axe des abscisses.

On peut déterminer cet angle en calculant d'abord le coefficient directeur de cette droite, puis en divisant le changement dans la direction y par le changement dans la direction x, ensuite en trouvant l'inverse de la tangente du coefficient directeur.