Calculateur de distance

Avez-vous déjà voulu calculer la distance d'un point à un autre, ou la distance entre deux villes ? Vous êtes-vous déjà demandé quelle était la définition de la distance ? Nous avons les réponses à toutes ces questions et plus encore, y compris une explication détaillée de la façon de calculer la distance entre deux objets quelconques dans l'espace 2D. En prime, nous vous proposons un sujet fascinant sur la manière dont nous percevons les distances, par exemple sous la forme d'une différence en pourcentage. Nous sommes sûrs que vous allez adorer !

Vous êtes plutôt du genre à regarder une vidéo que de lire un pavé ? Apprenez tout ce dont vous avez besoin en 90 secondes grâce à cette vidéo que nous avons réalisée pour vous :

Avant d'aborder le calcul des distances, il convient de préciser ce qu'est une distance. La définition la plus courante est l'espace unidimensionnel entre deux points. Cette définition est une façon de dire ce que la plupart d'entre nous pensent intuitivement de la distance, mais ce n'est pas la seule façon de parler de la distance. Vous verrez dans les sections suivantes comment le concept de distance peut être étendu au-delà de la longueur. Le concept de distance peut être multiple ; c'est notamment cette notion qui se cache derrière la théorie de la relativité d'Einstein.

Si nous nous en tenons à la définition géométrique de la distance, nous devons encore définir le type d'espace dans lequel nous travaillons. Dans la plupart des cas, il s'agit probablement d'un espace à trois dimensions ou moins, puisque c'est tout ce que nous pouvons imaginer sans que notre cerveau n'explose. Pour ce calculateur, nous nous concentrons sur la distance en 2D (la distance en 1D étant un cas particulier). Si vous cherchez la distance 3D entre 2 points, nous vous encourageons à utiliser notre calculateur de distance en 3D 🇺🇸 spécialement conçu à cet effet.

Pour trouver la distance entre deux points, la première chose dont vous avez besoin est de deux points… Forcément. Ces points sont décrits par leurs coordonnées dans l'espace. Pour chaque point dans l'espace 2D, nous avons besoin de deux coordonnées qui sont uniques à ce point. Si vous souhaitez trouver la distance entre deux points dans l'espace 1D, vous pouvez toujours utiliser ce calculateur en entrant simplement les deux mêmes coordonnées pour les deux points. Comme il s'agit d'un cas très particulier, nous ne parlerons dorénavant que de la distance dans un plan à deux dimensions.

L'étape suivante, si vous voulez être mathématique, précis et exact, est de définir le type d'espace dans lequel vous travaillez. Non, attendez, ne vous enfuyez pas ! C'est plus simple que vous ne le pensez. Si vous ne savez pas dans quel espace vous travaillez ou si vous ne saviez même pas qu'il existait plus d'un type d'espace, vous travaillez très probablement dans l'espace euclidien. En effet, c'est l'espace « par défaut » dans lequel nous effectuons presque toutes les opérations géométriques, et c'est celui sur lequel nous avons fixé l'ensemble des opérations du calculateur. Regardons plus en détail l'espace euclidien : qu'est-ce que c'est ? Quelles sont ses propriétés ? Et pourquoi est-il si important ?

L'espace euclidien ou la géométrie euclidienne est ce que nous pensons tous habituellement de l'espace 2D avant de recevoir une formation mathématique approfondie. Dans l'espace euclidien, la somme des angles d'un triangle est égale à 180º et les carrés ont tous leurs angles égaux à 90º. Toujours. C'est quelque chose que nous prenons tous pour acquis, mais ce n'est pas vrai dans tous les espaces. Ne confondons pas non plus l'espace euclidien avec les espaces multidimensionnels. L'espace euclidien peut avoir autant de dimensions que vous voulez, tant qu'il y en a un nombre fini, et que ces dernières obéissent toujours aux règles euclidiennes.

Nous ne voulons pas vous ennuyer avec des définitions mathématiques de ce qu'est un espace et de ce qui rend l'espace euclidien unique, car cela serait trop compliqué à expliquer pour un simple calculateur de distance. Cependant, nous pouvons essayer de vous donner quelques exemples d'autres espaces qui sont couramment utilisés et qui pourraient vous aider à comprendre pourquoi l'espace euclidien n'est pas le seul espace. De plus, vous comprendrez, avec un peu de chance, pourquoi nous n'allons pas nous embêter à calculer des distances dans d'autres espaces.

Le premier exemple que nous vous présentons est un peu obscur, mais nous espérons que vous nous excuserez, puisque nous sommes physiciens, de commencer par ce type d'espace très important : L'espace de Minkowski. La raison pour laquelle nous l'avons choisi est qu'il est très courant en physique, en particulier il est utilisé dans la théorie de la relativité, la relativité générale et même dans la théorie quantique des champs relativiste. Cet espace est très similaire à l'espace euclidien, mais s'en distingue par une caractéristique très cruciale : l'addition du produit scalaire (à ne pas confondre avec le produit vectoriel).

L'espace euclidien et l'espace de Minkowski sont tous deux ce que les mathématiciens appellent des espaces plats. Cela signifie que l'espace lui-même a des propriétés planes ; par exemple, la plus courte distance entre deux points quelconques est toujours une droite (consultez le calculateur d'interpolation linéaire 🇺🇸). Il existe cependant d'autres types d'espaces mathématiques appelés espaces courbes dans lesquels l'espace est intrinsèquement courbe et la distance la plus courte entre deux points n'est pas une droite.

Cet espace courbe est difficile à imaginer en 3D ; mais pour les espaces 2D, nous pouvons imaginer qu'au lieu d'avoir une aire plane, nous avons un espace 2D, par exemple, courbé comme la surface d'une sphère. Dans ce cas, des choses très étranges se produisent. La distance la plus courte d'un point à un autre n'est pas une ligne droite, car toute droite dans cet espace est courbée en raison de la courbure intrinsèque de l'espace. Une autre caractéristique de cet espace est que certaines droites parallèles 🇺🇸 se rencontrent réellement en un point. Vous pouvez essayer de le comprendre en pensant aux lignes de longitude qui divisent la Terre en plusieurs fuseaux horaires et se croisent aux pôles.

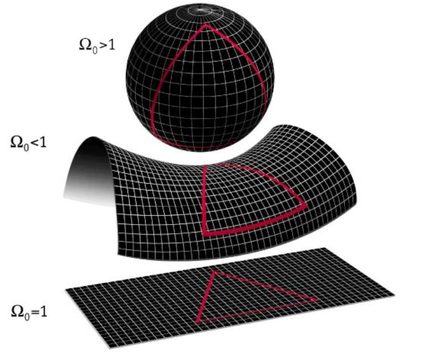
Il est important de noter que ceci est conceptuellement TRÈS différent d'un changement de coordonnées. Lorsque nous prenons les coordonnées standard $x, y, z$ et que nous les convertissons en coordonnées polaires, cylindriques ou même sphériques, nous restons dans l'espace euclidien. Lorsque nous parlons d'un espace courbe, nous parlons d'un espace très différent en termes de propriétés intrinsèques. En coordonnées sphériques, vous pouvez toujours avoir une droite et la distance se mesure aussi toujours en ligne droite, même si cela serait très difficile à exprimer en chiffres.

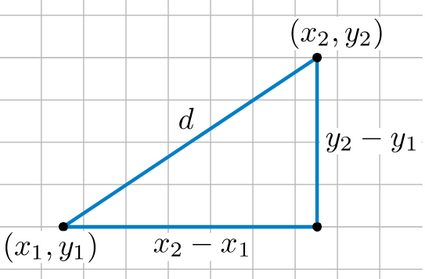
Pour en revenir à l'espace euclidien, nous pouvons maintenant vous présenter la formule de distance que nous vous avons promise au début. La formule de la distance est la suivante :

Elle se rapporte au théorème de Pythagore, selon lequel $a^2+b^2=c^2$. Ici, $a$ et $b$ sont les côtés adjacents d'un triangle rectangle et $c$ est l'hypoténuse. Supposons que deux points, $(x_1, y_1)$ et $(x_2, y_2)$, soient les coordonnées des extrémités de l'hypoténuse. Alors $(x_2 - x_1)^2$ dans l'équation de la distance correspond à $a^2$ et $(y_2 - y_1)^2$ correspond à $b^2$. Puisque $c = \sqrt{a^2 + b^2}$, vous pouvez voir pourquoi il s'agit simplement d'une extension du théorème de Pythagore.

La formule de distance que nous venons de voir est la formule standard de la distance euclidienne, mais si vous y réfléchissez, elle peut sembler un peu limitée. Souvent, nous ne voulons pas seulement trouver la distance entre deux points. Parfois, nous voulons calculer la distance d'un point par rapport à une droite ou à un cercle. Dans ces cas-là, nous devons d'abord définir quel point de cette droite ou de cette circonférence, nous allons utiliser pour le calcul de la distance, puis utiliser la formule de distance que nous avons vue juste au-dessus.

C'est ici que le concept de droite perpendiculaire 🇺🇸 devient crucial. La distance entre un point et un objet continu est définie par la perpendicularité. D'un point de vue géométrique, la première étape pour mesurer la distance entre un point et un autre consiste à créer une droite entre les deux points, puis à mesurer la longueur de ce segment. Lorsque nous mesurons la distance entre un point et une droite, la question qui se pose est la suivante : « Parmi les nombreuses droites possibles, laquelle dois-je tracer ? ». Dans ce cas, la réponse est la suivante : la ligne partant du point qui est perpendiculaire à la première droite. Cette distance sera nulle dans le cas où le point est une partie de la droite. Pour ces cas à une dimension, on ne peut considérer que la distance entre les points, puisque la droite représente tout l'espace 1D.

Cela impose des restrictions sur la manière de calculer les distances dans certains cas géométriques intéressants. Par exemple, nous pourrions redéfinir le concept de hauteur d'un triangle comme étant simplement la distance entre un sommet et le côté opposé du triangle. Dans ce cas, l'aire du triangle est également redéfinie en termes de distance, puisque l'aire est une fonction de la hauteur du triangle.

Prenons quelques exemples dans l'espace 2D. Pour calculer la distance entre un point et une droite, nous pourrions procéder étape par étape (calculer le segment perpendiculaire à la droite entre la droite et le point, puis calculer sa longueur) ou nous pourrions simplement utiliser cette équation plutôt pratique :

Où la droite est donnée par $Ax+By+C = 0$ et le point est défini par $(x_1, y_1)$.

Le seul problème ici est qu'une droite est généralement donnée sous la forme $y=mx+b$, nous devrions donc convertir cette équation sous la forme vue précédemment :

Nous pouvons donc voir que $A=m$, $B=-1$ et $C=b$. L'équation précédente se retrouve donc avec les valeurs suivantes :

Pour la distance entre 2 droites, il suffit de calculer la longueur du segment qui va de l'une à l'autre et qui est perpendiculaire aux deux. Là encore, il existe une formule simple pour nous aider :

Si les droites sont $A_1x+B_1y+C_1=0$ et $A_2x+B_2y+C_2=0$. Nous pouvons également utiliser leur forme affine et obtenir :

pour les droites $y=m_1x+b_1$ et $y=m_2x+b_2$.

Notez que les deux droites doivent être parallèles car sinon elles se toucheraient en un point et leur distance serait alors $d=0$. C'est la raison pour laquelle les formules omettent la plupart des indices puisque pour les droites parallèles : $A_1=A_2=A$ et $B_1=B_2=B$ tandis que pour la fonction affine, les droites parallèles sont celles pour lesquelles $m_1=m_2=m$.

Comme nous l'avons déjà mentionné, la distance peut avoir plusieurs significations, c'est pourquoi nous avons prévu quelques options différentes pour vous dans ce calculateur. Vous pouvez calculer la distance entre un point et une droite, la distance entre deux droites (elles doivent toujours être parallèles), ou la distance entre des points dans l'espace. Lorsqu'il s'agit de calculer les distances entre deux points, vous avez la possibilité de le faire en 1, 2, 3 ou 4 dimensions. Oui, nous savons que 4 dimensions, ça fait peur, mais vous n'avez pas besoin d'utiliser cette option. Et vous pouvez toujours en apprendre davantage en lisant quelques ressources intéressantes et en jouant avec le calculateur. Nous vous promettons que cela ne cassera pas Internet ou l'univers.

Nous avons également ajouté la possibilité de définir 3 points différents dans l'espace, à partir desquels vous obtiendrez les 3 paires des distances qui les séparent. Ainsi, si vous avez plus de deux points, vous gagnerez du temps. Le nombre de dimensions dans lesquelles vous travaillez déterminera le nombre de coordonnées qui décrivent un point, c'est pourquoi, au fur et à mesure que vous augmentez le nombre de dimensions, le calculateur vous demandera plus de valeurs à entrer.

Bien que l'utilisation du calculateur soit très simple, nous avons tout de même décidé d'inclure une solution étape par étape. De cette façon, vous pouvez vous familiariser avec la formule de distance et la façon de l'utiliser (comme si nous étions dans les années 1950 et qu'Internet n'existait pas encore). Jetons maintenant un coup d'œil à un exemple pratique : comment trouver la distance entre deux points en 2D ?

Supposons que vous disposiez de deux coordonnées, $(3, 5)$ et $(9, 15)$, et que vous souhaitiez calculer la distance qui les sépare. Pour calculer la distance en 2D entre ces deux points, procédez comme suit :

1. Entrez les valeurs dans la formule : $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$.
2. Dans la formule, faites la soustraction des valeurs entre parenthèses.
3. Élevez au carré les deux quantités entre parenthèses.
4. Additionnez les résultats.
5. Prenez la racine carrée.
6. Utilisez le calculateur de distance pour vérifier vos résultats.

En calculant l'exemple à la main, vous obtenez :

Ce qui est égal à environ $11,\!66$. Notez que lorsque vous prenez la racine carrée, vous obtenez un résultat positif et un résultat négatif, mais comme il s'agit d'une distance, vous ne vous intéressez qu'au résultat positif. Le calculateur effectuera ces calculs étape par étape pour vous donner le résultat sous forme exacte et approximative.

Jetons un coup d'œil à l'une des applications du calculateur de distance. Supposons que vous voyagiez entre les villes A et B, et que le seul arrêt soit dans la ville C, avec une route A à B perpendiculaire à la route B à C. Nous pouvons déterminer la distance de A à B, et ensuite, en connaissant le prix de l'essence, déterminer le coût du carburant, le carburant utilisé et le coût par personne pendant le voyage. Le calculateur de carburant, que vous trouverez sur notre site, peut vous faciliter la tâche.

La distance entre les villes doit être calculée avec précision. Une ligne droite (comme celle que nous utilisons dans ce calculateur) peut être une bonne approximation, mais elle peut être assez erronée si l'itinéraire que vous prenez n'est pas direct, mais fait un détour, peut-être pour éviter des montagnes ou pour passer par une autre ville. Dans ce cas, utilisez Google maps ou tout autre outil qui calcule la distance le long d'un chemin et pas seulement la distance d'un point à un autre à vol d'oiseau.

Notre calculateur peut donner des calculs et des prédictions pour les distances entre les objets, pas pour la longueur d'un chemin. Ceci étant dit, il existe encore de nombreux scénarios dans lesquels vous pourriez être intéressé·e par la distance entre les objets, indépendamment du chemin que vous auriez à prendre. Un de ces exemples est la distance entre les objets astronomiques.

Lorsque l'on considère une distance sur Terre, il est difficile d'aller loin sans se heurter à certains problèmes, de la courbure intrinsèque de cet espace (due au fait que la courbure de la Terre n'est pas nulle) à la distance maximale limitée entre deux points sur la Terre. C'est pour cette raison, et aussi parce qu'il y a tout un univers au-delà de notre Terre, que les distances dans l'univers intéressent beaucoup de gens. Étant donné que nous ne disposons pas de moyens appropriés pour effectuer des voyages interplanétaires, et encore moins des voyages interstellaires, concentrons-nous pour l'instant sur la distance euclidienne réelle de certains objets célestes. Par exemple, la distance entre la Terre et le Soleil, ou la distance entre la Terre et la Lune.

Ces distances sont inimaginables pour nos cerveaux de primates. Nous avons du mal à comprendre la taille de notre planète, sans parler de l'univers vaste et infini. C'est si difficile que nous devons utiliser la notation scientifique ou les années-lumière, comme unité de distance pour des longueurs aussi grandes. Les plus longs voyages que vous puissiez faire sur Terre sont à peine de quelques milliers de kilomètres, alors que la distance entre la Terre et la Lune, l'objet astronomique le plus proche de nous, est de 384 000 km. En outre, la distance qui nous sépare de notre étoile la plus proche, c'est-à-dire la distance de la Terre au Soleil, est de 150 000 000 km, soit un peu plus de 8 minutes-lumière.

Si l'on compare ces distances à celle de notre deuxième étoile la plus proche (Alpha du Centaure), qui est de 4 années-lumière, elles commencent soudain à paraître beaucoup plus petites. Pour exagérer encore la comparaison, nous pouvons toujours penser à un vol de New York à Sydney, qui prend généralement plus de 20 heures et qui n'est que de 16 000 km environ. Maintenant, comparez cette distance à la taille de l'univers observable, qui est d'environ 46 600 000 000 d'années-lumière !

Ici, nous avons par inadvertance levé un point fascinant, à savoir que nous mesurons les distances non pas en longueur, mais en temps. Ainsi, nous étendons la notion de distance au-delà de son sens géométrique. Nous explorerons cette possibilité dans la section suivante, lorsque nous parlerons de l'importance et de l'utilité de la distance au-delà du sens purement géométrique. C'est une notion très intéressante qui s'inspire principalement du besoin philosophique d'étendre chaque concept pour lui donner une signification universelle. Pensez à la théorie physique évidente à mentionner, lorsqu'on parle de permutations de l'espace et du temps, ou de toute autre variable pouvant être mesurée.

Généralement, le concept de distance fait référence à la distance géométrique euclidienne et est lié à la longueur. Cependant, vous pouvez étendre la définition de distance pour qu'elle signifie simplement la différence entre deux choses, et un monde de possibilités s'ouvre alors. Tout à coup, on peut décider quelle est la meilleure façon de mesurer la distance entre deux choses et de l'exprimer en termes de quantité la plus utile. Par exemple, pensez à la distance entre deux nombres, qui n'est rien d'autre que la différence dans l'espace 1D entre ces nombres. Pour l'obtenir, il suffit de soustraire l'un de l'autre et le résultat sera la différence, c'est-à-dire la distance.

Nous pourrions passer de cette distance numérique à, par exemple, la différence ou la distance en termes de pourcentage de différence, qui dans certains cas pourrait fournir un meilleur moyen de comparaison. Il ne s'agit encore que d'un niveau d'abstraction dans lequel nous supprimons simplement les unités de mesure. Mais que se passerait-il si nous utilisions des unités complètement différentes ?

En étendant le concept de distance à un quelque chose de plus proche de la différence, nous pouvons calculer la différence entre deux températures, ou d'autres quantités connexes comme la pression. Mais il n'est pas nécessaire de tomber dans l'extrême, voyons comment deux points peuvent être séparés par une distance différente, en fonction des hypothèses formulées. Pour en revenir à l'exemple de la distance de conduite, nous pourrions mesurer la distance du trajet en temps, au lieu de la longueur. Dans ce cas, nous avons besoin d'une hypothèse pour permettre une telle transposition, à savoir le moyen de transport.

Il y a une grande différence entre le temps nécessaire pour parcourir 10 km en avion et le temps qu'il faut pour parcourir 10 km en voiture. Parfois, cependant, l'hypothèse est claire et implicitement acceptée, comme lorsque nous mesurons la distance de l'éclair en unité de temps que nous convertissons ensuite en longueur. Cela soulève un point intéressant : le facteur de conversion entre les distances en unité de temps et en unité de longueur est ce que nous appelons la « vitesse » ou la « vélocité » (souvenez-vous qu'il ne s'agit pas exactement de la même chose). À vrai dire, cette vitesse ne doit pas nécessairement être constante, comme en témoignent les mouvements accélérés tels que celui d'une chute libre sous l'effet de la force gravitationnelle. Pensez aussi au mouvement qui relie le temps et la distance d'arrêt via la force de rupture et la traînée ou, dans des cas très extrêmes, via la force d'un accident de voiture.

Un autre endroit où vous pouvez trouver des unités de distance bizarres est la physique du solide, où la distance parcourue par une particule à l'intérieur d'un matériau est souvent exprimée comme une moyenne d'interactions ou de collisions. Cette distance est reliée à la longueur en utilisant le libre parcours moyen, qui est la distance moyenne (en longueur) qu'une particule parcourt entre deux interactions. Si nous voulons être encore plus exotiques, nous pouvons penser à la distance entre la valeur actuelle et la valeur future d'un objet, comme une voiture.

Nous ne voulons cependant pas faire fondre le cerveau de qui que ce soit, alors s'il vous plaît ne réfléchissez pas trop à ce sujet. Prenez simplement ce calculateur et utilisez-le pour une distance basée sur la longueur dans un espace 2D. Vous pouvez toujours revenir à cette vision philosophique des distances si vous vous ennuyez !

Pour trouver la distance entre deux points, nous utiliserons la formule de la distance : √[(x₂ - x₁)² + (y₂ - y₁)²].

1. Obtenez les coordonnées des deux points dans l'espace.
2. Soustrayez les coordonnées x d'un point à l'autre, idem pour les composantes y.
3. Élevez au carré les deux résultats séparément.
4. Additionnez les valeurs obtenues à l'étape précédente.
5. Trouvez la racine carrée du résultat ci-dessus.

Si vous pensez que cela demande trop d'efforts, vous pouvez simplement utiliser le calculateur de distance d'Omni Calculator.

La distance n'est pas un vecteur. La distance entre des points est une quantité scalaire, ce qui signifie qu'elle n'est définie que par sa valeur. En revanche, le déplacement est un vecteur avec une valeur et une direction. Ainsi, la distance entre A et B est la même que la distance de B à A, mais le déplacement est différent en fonction de leur ordre.

Pour évaluer la distance qui vous sépare d'un orage, divisez par 3 le nombre de secondes entre l'éclair et le tonnerre. Par exemple, si vous voyez un éclair et entendez le tonnerre 9 secondes plus tard, vous vous trouvez à environ 3 km de l'orage.

La formule de la distance est la suivante : √[(x₂ - x₁)² + (y₂ - y₁)²]. Cela fonctionne pour deux points quelconques dans l'espace 2D avec les coordonnées (x₁, y₁) pour le premier point et (x₂, y₂) pour le second point. Pour mémoriser facilement l'équation, il suffit de voir qu'il s'agit du théorème de Pythagore. La distance représente l'hypoténuse, tandis que les longueurs des côtés adjacents sont les différences entre les composantes x et y des points.

La distance d'un vecteur est sa norme. Si vous connaissez ses composantes :

1. Prenez chacune des composantes du vecteur et élevez-les au carré.
2. Résumez-les.
3. Trouvez la racine carrée du résultat précédent.
4. Bon travail !

Si vous connaissez sa représentation polaire, il s'agira d'un nombre et d'un angle. Ce nombre est la norme du vecteur, qui est sa distance.

L'unité SI de distance est le mètre, abrégé en « m ». Un mètre équivaut à environ 3,28 ft. Les autres unités courantes du Système international sont le centimètre (un centième de mètre, soit 0,39 in) et le kilomètre (mille mètres, soit 0,62 mi), entre autres.

La distance de A à B est la longueur de la droite allant de A à B. La distance de B à A est la même que la distance de A à B car la distance est un scalaire

La distance est une mesure de l'espace unidimensionnel. La distance entre deux points est la plus petite longueur de l'espace unidimensionnel qui les sépare. Si vous divisez la distance par le temps, vous obtiendrez la vitesse, qui a pour dimensions l'espace et le temps.

Une année-lumière est une mesure de distance. Elle correspond à 9,461×10¹² kilomètres ou 5,879×10¹² miles, soit la distance parcourue par un rayon de lumière dans un vide parfait en l'espace d'une année.

La vitesse et le temps de déplacement d'un objet permettent de calculer la distance.

1. Assurez-vous que la vitesse et le temps ont des unités compatibles (vitesse en kilomètres par heure avec le temps en heures, mètres par seconde avec des secondes, etc.).
2. Si ce n'est pas le cas, convertissez-les dans les unités nécessaires.
3. Multipliez la vitesse par le temps.
4. Le résultat devrait être la distance parcourue dans l'unité de longueur utilisée pour votre vitesse !