Calculateur d'aire d'un pavé droit

Bienvenue sur le calculateur d'aire d'un pavé droit, où vous aurez l'occasion de tout savoir sur ce prisme si particulier. Le pavé droit a de nombreux noms : prisme droit, prisme à base rectangulaire, parallélépipède rectangle. Ne soyez pas surpris•e de le voir changer de nom au fil du texte. Nous allons vous expliquer comment trouver l'aire d'un pavé droit. Vous voulez peindre une grange et vous vous demandez la quantité de peinture nécessaire 🇺🇸 ? Ou bien, vous construisez une piscine dans votre jardin et vous voulez déterminer le nombre de carreaux dont vous avez besoin ?

Quelle que soit la question, tant qu'elle se résume à l'aire d'un pavé droit, vous êtes au bon endroit !

Avant de voir quelle est l'aire d'un pavé droit, nous devons nous familiariser avec le prisme lui-même.

Imaginez une boîte : une boîte rectangulaire normale, comme une boîte à chaussures. Eh bien, il s'agit d'un pavé droit ! Ou bien souvenez-vous de ces dessins de maisons que nous faisions tous à la maternelle ? Retirez le toit pointu et vous avez un autre exemple de pavé droit ou parallélépipède rectangle.

D'un point de vue mathématique, un pavé droit, ou de son nom plus technique, un prisme droit à base rectangulaire, est un solide dont les six côtés sont des rectangles perpendiculaires les uns aux autres. Cela signifie notamment qu'il y a trois paires de faces identiques placées sur les côtés opposés du solide.

Par ailleurs, comme pour toute autre définition scientifique, il existe quelques noms savants associés au prisme. Les faces inférieure et supérieure du prisme sont appelées bases, et les quatre autres sont les faces latérales. Enfin, les bords de chaque rectangle sont les arêtes.

Il est temps de mettre de côté les grands mots et de se concentrer sur la façon de trouver l'aire d'un pavé droit.

Pour savoir quelle est l'aire d'un pavé droit, nous devons connaître ses trois côtés. Commençons par déterminer leur notation pour notre calculateur d'aire d'un pavé droit :

• L – longueur de la base (la plus longue arête de la base)
• l – largeur de la base (la plus petite arête de la base)
• h – hauteur du pavé droit (arête latérale)
• A_b – aire de la base du pavé droit
• A_l – aire des faces latérales du pavé droit
• A – aire totale du pavé droit
• V – volume du pavé droit

Notez que A_b représente l'aire d'une seule base de notre prisme, alors que A_l désigne l'aire latérale, c'est-à-dire l'aire totale des quatre faces latérales. Par conséquent, puisque le solide a deux bases (celle du bas et celle du haut), la formule de l'aire d'un pavé droite est la suivante :

Aire totale = 2 × aire de la base + aire latérale

Ce qui, dans notre notation, se traduit par :

A = 2 × A_b + A_l

Rappelez-vous que, pour notre calculateur, toutes les faces sont des rectangles et que, comme indiqué dans le calculateur d'aire d'un rectangle, on les calcule en multipliant la largeur de leurs côtés par leur longueur. Utilisons maintenant ces informations pour étudier la base de notre prisme. D'après notre notation, c'est un rectangle dont les côtés sont L et l, donc son aire est L × l. Et c'est précisément la formule pour l'aire de la base :

A_b = L × l

Un jeu d'enfant, n'est-ce pas ? Eh bien, essayons désormais de faire quelque chose d'un peu plus compliqué et regardons de plus près l'aire latérale. Nous avons quatre faces qui contribuent à cette mesure, et toutes sont des rectangles. De plus, parmi ces quatre faces, il y a deux paires de faces identiques (le côté avant et le côté arrière, et le côté gauche et le côté droit). Toutes ces paires ont une largeur égale à h, l'arête latérale (ou la hauteur) du prisme. L'une de ces paires de rectangles a une longueur égale à la première dimension de la base, L, et l'autre a une longueur égale à la deuxième dimension de la base, l. Au total, nous obtenons que l'aire latérale, ou A_l comme nous l'appelons, est :

A_l = L × h + L × h + l × h + l × h

Ou simplement :

A_l = 2 × L × h + 2 × l × h

Ainsi, en ajoutant l'aire de la base, cela nous permet d'écrire la formule de l'aire d'un pavé droit :

A = 2 × A_b + A_l = 2 × L × l + 2 × L × h + 2 × l × h

Disons que vous vouliez carreler une piscine et que vous souhaitiez déterminer la superficie à carreler. Si la piscine est rectangulaire avec un fond plat, il s'agit précisément d'un pavé droit ! Regardons une jolie image pour y voir plus clair.

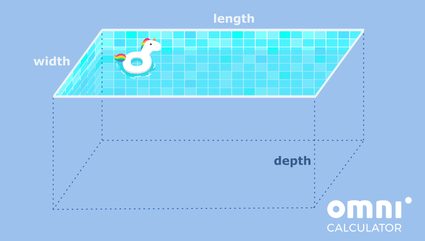
D'accord, nous savons qu'il est difficile de détourner les yeux de la licorne flottante, mais revenons au problème principal !

Disons que la piscine a une longueur de 10 m, une largeur de 5 et une profondeur de 2 m. Maintenant que nous avons ses dimensions, essayons de les exprimer selon la notation que nous avons utilisée plus haut.

Tout d'abord, les côtés de la base de notre piscine sont sa longueur et sa largeur, qui, dans notre cas, sont respectivement de 10 et 5 m. Puisque nous utilisons L et l comme arête de la base, nous pouvons entrer ses nombres dans notre calculateur L = 10 m et l = 5 m. Notez que l'ordre dans lequel nous saisissons ces valeurs n'a pas d'importance. Cela revient seulement à regarder la piscine sous un autre angle et ne change pas son aire.

Il ne nous reste plus qu'à entrer la profondeur de la piscine dans notre calculateur dans le champ h. Et c'est exactement ce que nous devrions faire maintenant : saisissez h = 2 m. Ce qui correspond aussi bien à la profondeur de la piscine qu'à la hauteur du prisme.

Enfin fini ? Eh bien, pas exactement. Avec notre calculateur d'aire d'un pavé droit, on obtient :

A = 2 × L × l + 2 × L × h + 2 × l × h = 2 × 10 m × 5 m + 2 × 10 m × 2 m + 2 × 5 m × 2 m = 160 m²

Mais il s'agit de l'aire de l'ensemble du prisme, et nous ne voulons pas carreler 🇺🇸 la piscine en entier. Après tout, si nous posons des carreaux sur le dessus, il sera assez difficile d'y entrer (ou d'y sortir), n'est-ce pas ? Il s'agirait là d'une malveillance de haut vol, pire encore que la suppression de l'échelle pour vos Sims.

Pour trouver la bonne réponse, activez le Mode avancé (Advanced mode). Il nous permet de voir l'aire de la base et l'aire latérale du solide, séparément. Comme vous savez maintenant trouver l'aire d'un prisme droit, soit :

A = 2 × A_b + A_l

Il suffit de soustraire l'aire supplémentaire que nous n'allons pas carreler. Et c'est la face supérieure. Mais la base du haut est la même que celle du bas, donc la superficie que nous devons carreler est, en fait :

superficie à carreler = A - A_b

Ce qui, dans notre cas, est :

superficie à carreler = 160 m² - 50 m² = 110 m²

Voilà ce qui nous rapproche un peu plus de la finition de notre piscine et de la possibilité d'admirer votre travail en buvant une bière bien fraîche. Cela dit, le pavé droit n'est pas la seule forme 3D à base rectangulaire. Pour en savoir plus, consultez le calculateur d'aire d'une pyramide à base rectangulaire 🇺🇸.