Calculateur d'aire d'un rectangle

Que vous ayez besoin de connaître l'aire d'un tapis, d'un colis, d'un écran de télévision, d'une piscine ou d'une fenêtre, ce calculateur d'aire d'un rectangle résoudra votre problème en un clin d'œil !

Après avoir lu cet article, vous saurez enfin :

• comment calculer l'aire d'un rectangle ;
• comment trouver le périmètre d'un rectangle ;
• comment calculer la diagonale d'un rectangle.

Alors, poursuivez votre lecture pour en apprendre plus sur cette forme géométrique qu'est le rectangle. Nous allons passer en revu la définition, les formules et même les propriétés de ce dernier… Le calcul de l'aire d'un rectangle n'aura plus de secret pour vous !

De manière générale, on dit qu'un rectangle est un quadrilatère avec quatre angles droits. Mais on peut aussi le définir comme un parallélogramme contenant un angle droit (si un angle est droit, les autres doivent l'être aussi). De plus, chaque côté d'un rectangle a la même longueur que celui qui lui est opposé. Les côtés adjacents peuvent être inégaux, contrairement au carré, qui est un cas particulier de rectangle.

Avec juste un peu de notion de latin, on peut généralement déduire beaucoup de choses du nom des formes géométriques. Le mot rectangle vient du latin rectangulus. Il s'agit d'une combinaison de rectus (qui signifie « droit ») et de angulus (un angle), qui peut donc servir de définition simple et élémentaire pour le rectangle.

Un rectangle est un exemple de quadrilatère. Vous pouvez utiliser notre calculateur de quadrilatères 🇺🇸 pour trouver l'aire d'autres types de quadrilatères.

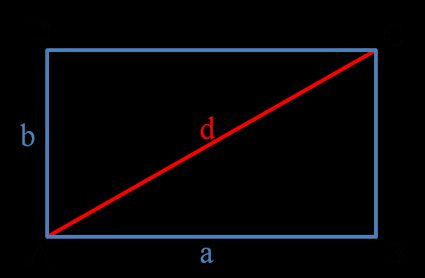
L'image ci-dessus montre un rectangle quelconque. Il a quatre côtés et quatre angles droits. Les longueurs des côtés sont indiquées par a et b, tandis que la longueur de la diagonale est indiquée par d.

Si tous les côtés du rectangle ont la même longueur, nous parlons de carré.

L'aire d'un rectangle est l'espace délimité par ses côtés ou, en d'autres termes, la zone à l'intérieur du périmètre d'un rectangle. Pour calculer l'aire d'un rectangle, il suffit de multiplier ses côtés a et b :

aire = a × b

Notre calculateur d'aire d'un rectangle utilise les formules d'aire suivantes :

• Formule de l'aire d'un rectangle :
  A = a × b

• Formule du périmètre d'un rectangle :
  P = 2 × (a + b)

• Formule de la diagonale d'un rectangle :
  d² = a² + b²
d = √(a² + b²)

Voici comment effectuer le calcul de l'aire d'un rectangle à partir de la formule de son aire, A = a × b :

1. Choisissez la longueur du rectangle : par exemple, a = 5 cm.
2. Choisissez la largeur du rectangle : par exemple, b = 6 cm.
3. Multipliez ces deux valeurs : A = 5 cm × 6 cm = 30 cm².
4. L'aire du rectangle est de 30 cm² .

Voyons comment trouver le périmètre d'un rectangle. Souvenez-vous, le périmètre est la somme de tous les côtés d'une forme géométrique :

P = a + b + a + b

Ce qui peut s'écrire comme suit :

P = 2 × (a + b)

Prenons le même rectangle comme exemple :

1. Choisissez la longueur du rectangle : a = 5 cm dans notre cas.
2. Choisissez la largeur du rectangle : par exemple, b = 6 cm.
3. Additionnez ces deux valeurs : a + b = 5 + 6 = 11 cm.
4. Multipliez le résultat par 2 : P = 2 × 11 = 22 cm.
5. Et voilà ! Le périmètre de notre rectangle est de 22 cm.

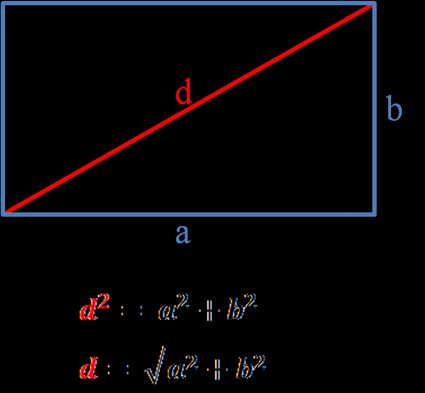
La diagonale d'un rectangle est un segment qui relie deux sommets opposés d'un rectangle. Mais comment calculer la diagonale d'un rectangle​ ? Prenons un exemple !

1. Choisissez la longueur du rectangle : par exemple, a = 5 cm.
2. Déterminez la largeur du rectangle : par exemple, b = 6 cm.
3. Élevez a au carré : a² = 25 cm².
4. Élevez b au carré : b² = 36 cm².
5. Additionnez ces deux valeurs : a² + b² = 25 + 36 = 61 cm².
6. Enfin, prenez la racine carrée du résultat : d = √(a² + b²) = √61 ≈ 7,81 cm.
7. Et voilà comment effectuer le calcul de la diagonale d'un rectangle ! La longueur de la diagonale est donc d'environ 7,81 cm.

Naturellement, au lieu de calculer toutes ces valeurs à la main, vous pouvez utiliser ce calculateur d'aire d'un rectangle. Vous pouvez également l'utiliser dans l'autre sens, par exemple, pour calculer la largeur d'un rectangle dont la longueur et le périmètre sont connus.

La figure ci-dessus montre un type spécial de rectangle appelé rectangle d'or. Apprenez-en plus avec notre calculateur du rectangle d'or 🇺🇸. Un tel rectangle remplit la condition suivante :

(a + b) / a = a / b = ϕ

où φ est le nombre d'or égal à 1,618. Pour en savoir plus sur ce rapport spécial, consultez notre calculateur du nombre d'or.

Comme vous vous en souvenez probablement grâce à notre calculateur de ratio, un rapport (ou ratio) est une relation entre deux quantités, souvent représentée sous la forme d'une fraction.

Saviez-vous que vous pouvez construire le rectangle d'or en utilisant uniquement une règle et un compas ? Il suffit de quelques étapes !

1. Tracez un carré.
2. Tracez un segment entre le milieu d'un côté du carré et le coin opposé. Notre calculateur de point médian peut vous aider pour cette étape.
3. Tracez un cercle dont le rayon est égal à la longueur du segment et dont le centre est le point médian, comme dans l'image ci-dessus.
4. Le point où le cercle rencontre le côté prolongé du carré est le prochain coin du rectangle d'or.
5. Trouvez le dernier sommet et complétez le rectangle d'or.

Taadaaa ! Ce n'était pas si difficile, n'est-ce pas ?

Les rectangles ont de nombreuses propriétés intéressantes.

• Cyclique : tous les coins sont situés sur un même cercle.
• Equiangulaire : tous ses angles sont égaux à 90 degrés.
• Rectiligne : ses côtés se rencontrent à angle droit.
• Deux axes de symétrie : un vertical et un horizontal qui passent par le centre qui divisent le rectangle en deux parties égales.
• Deux diagonales qui se coupent en leur milieu : vous pouvez trouver la longueur des diagonales à l'aide du théorème de Pythagore.

Autres propriétés moins connues des rectangles :

• L'intersection des diagonales est le centre du cercle circonscrit. Il existe un cercle dont le centre est situé à cet endroit et qui passe par les quatre coins.
• Dans un rectangle dont les côtés sont de différentes longueurs (ce n'est donc pas un carré), il n'est pas possible de tracer un cercle inscrit.
• Les lignes joignant les milieux des côtés d'un rectangle forment un losange, dont l'aire est égale à la moitié de celle du rectangle. Les côtés de ce losange sont parallèles aux diagonales.

Vous pouvez également créer vos propres propriétés. Par exemple, imaginez faire tourner un rectangle autour de l'un de ses côtés, eh bien, vous obtenez un cylindre.

On répond à vous interrogations :

1. Un carré est-il un rectangle ? OUI.
2. Un rectangle est-il un parallélogramme ? OUI.
3. Un rectangle est-il un losange ? En général : NON. Seulement si c'est un carré (alors les angles du losange sont tous de 90 degrés).
4. Un losange est-il un rectangle ? En général : NON. Uniquement s'il s'agit d'un carré (alors, les côtés du rectangle sont tous de même longueur).
5. Un rectangle est-il un quadrilatère ? OUI, bien sûr.
6. Un rectangle est-il un trapèze ? OUI.

Vous vous demandez toujours si un carré est un rectangle ou si un rectangle est un parallélogramme ? Regardez l'image ci-dessous et vous n'aurez plus aucun doute sur les relations entre les différents quadrilatères :

Comment lire ce diagramme ? Commençons par notre rectangle. Trois figures sont directement liées à cette forme : un carré, un parallélogramme et un trapèze isocèle. Si la forme est au-dessus de notre forme d'intérêt, comme le carré est au-dessus du rectangle, cela signifie que toutes les propriétés du carré sont aussi présentes dans le rectangle. Nous pouvons dire que :

• Tout carré est un rectangle et un carré est un cas particulier de rectangle.

Pour les deux autres figures, nous pouvons dire de manière analogique :

• Tout rectangle est un parallélogramme et un rectangle est un cas particulier de parallélogramme.
• Chaque rectangle est un trapèze et un rectangle est un cas particulier de trapèze.

Il existe de nombreux classements qui évaluent les pays en fonction de leur superficie, de leur population, de leur niveau d'éducation ou de leurs lauréats du prix Nobel.

Mais vous êtes-vous déjà demandé qui est le vainqueur du concours du pays le plus rectangulaire ? Un géostatisticien australien, David Barry, a calculé le paramètre de « rectangularité » pour tous les pays du monde et a établi un classement.

Il en ressort que le pays le plus rectangulaire est l'Égypte, tandis que le titre du « pays le moins rectangulaire du monde » revient aux Maldives (l'auteur admet toutefois que les calculs pour les pays constitués de nombreuses petites îles peuvent être terriblement erronés). Consultez le tableau ci-dessous et découvrez les dix premiers pays les plus, ainsi que les moins rectangulaires.

L'Égypte est en tête, mais cela ne devrait surprendre personne si l'on considère la forme de ce pays sur la carte. Les États-Unis se situent en milieu de classement, principalement en raison de l'excentricité de l'Alaska et d'Hawaï. Ce qui est déroutant, c'est que le deuxième pays le plus rectangulaire, le Vatican, est en même temps le quatrième pays le plus arrondi. La Pologne, par exemple, est cinquième dans le classement de la « rondeur », et neuvième dans celui de la « rectangularité ».

Comment est-il possible d'être à la fois rectangulaire et arrondi ? Comme vous pouvez le deviner, tout dépend de la définition de la « rectangularité » et de la « rondeur », qui peut ne pas convenir à des formes complexes ou dispersées. Les frontières des pays sont généralement de tels exemples, ayant à la fois des frontières nettes, des petites îles et des colonies quelque part à l'autre bout du globe.

Si le sujet vous intéresse, vous pouvez consulter cette explication et discussion des résultats.

On pourrait penser que le monde serait plus facile à dessiner si chaque pays était un rectangle… Mais est-ce vraiment le cas ?

La forme rectangulaire est utilisée dans de nombreux motifs de la vie de tous les jours. Elle peut être utilisée pour des murs de briques, des carreaux de sol, des pavés ou différentes mosaïques. Vous trouverez ci-dessous quelques motifs populaires :

• Motif en pile : c'est le motif de carrelage le plus courant et le plus simple, car les carreaux sont posés en lignes droites.

• Motif à demi-brique : c'est un motif typique pour les chaussées, les carreaux et les briques.

• Motif en chevron : les parquets ont un bel aspect avec ce type de motif.

• Motif à effet tressé : souvent utilisé pour les couloirs ou les chemins extérieurs.

Bien entendu, il existe des carreaux de toutes formes et de toutes tailles, les hexagonaux et les octogonaux avec les carrés sont des choix très populaires. Pour le pentagone, la forme doit être irrégulière pour former un motif de carrelage.

Avez-vous une morphologie en H ? On parle aussi de morphologie en forme de rectangle. Pour le savoir, il vous suffit de mesurer votre poitrine, votre taille, vos hanches (là où elles sont le plus large) et le tour de vos hanches juste en dessous de votre taille. Puis, vous n'avez plus qu'à saisir ses valeurs dans le calculateur Omni. Vous obtiendrez alors des informations sur votre morphologie.

La morphologie en rectangle est définie comme un type de corps « masculin » car vos hanches, votre taille et votre poitrine sont à peu près de la même taille. Votre corps est bien proportionné et d'apparence athlétique.

Étonnamment, nous sommes entourés d'objets rectangulaires. C'est pourquoi notre calculateur de rectangles peut être utile non seulement pour les cours de mathématiques, mais aussi pour résoudre les problèmes de la vie quotidienne. Bien que le rectangle d'or ne puisse pas exister dans la réalité (car il faudrait qu'il soit parfaitement plat) il est possible d'en obtenir une approximation satisfaisante si la troisième dimension est négligeable par rapport aux deux autres.

• Nappes rectangulaires : en fonction de la taille de votre table, vous pouvez déterminer la nappe dont vous avez besoin ou la quantité de dentelle ou de ruban à ourler que vous devez utiliser.

• Portes ou vitres : une tempête ou une balle de golf a brisé la vitre de votre fenêtre ? Effectuez le calcul de l'aire d'un rectangle et estimez le coût de la réparation, en vous basant sur le prix au mètre carré.

• Écrans d'appareils électroniques (tablettes, smartphones, téléviseurs) : utilisez ce calculateur d'aire d'un rectangle pour estimer l'espace que prendra votre écran sur le mur, ou la taille de l'écran du téléphone que vous voulez acheter.

• Tableaux noirs, miroirs, cadres, toiles, feuilles de papier, cahiers, enveloppes, billets, drapeaux, piscines rectangulaires… La liste est interminable !

Jetez un coup d'œil autour de vous. Pouvez-vous trouver d'autres objets rectangulaires ? On est sûr•e que oui !