Calculateur du nombre d'or

Le calculateur du nombre d'or vous aidera à diviser un segment en deux parties de longueurs proportionnelles au nombre d'or. Avant de passer au calcul du nombre d'or, regardons de plus près sa définition. Dans les lignes qui suivent, vous trouverez tout ce qu'il faut savoir !

Vous pouvez également consulter le calculateur de proportion 🇺🇸 si vous souhaitez en savoir plus sur les rapports de proportionnalité – ou ratio – en général.

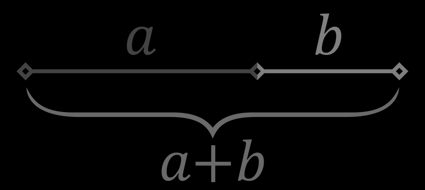
Le nombre d'or (également appelé section dorée, proportion dorée, ou encore divine proportion) apparaît lorsqu'un segment est divisé en deux parties. La proportion de la partie la plus longue par rapport à la partie la plus courte doit être la même que la proportion du segment entier par rapport à la partie la plus longue. Autrement dit, si la partie la plus longue est de longueur $a$ et la partie la plus courte de longueur $b$, la formule du nombre d'or se lit comme suit :

Pour calculer la valeur du nombre d'or, vous devez résoudre l'équation ci-dessus pour $a/b$. Il est pratique de la réarranger ainsi :

Il ne nous reste plus qu'à résoudre pour $x$ l'équation quadratique $x^2-x-1=0$ pour obtenir la valeur du nombre d'or, qui est égale à $\frac 12 (1+\sqrt{5})$, soit environ $1,618\, 033\, 988\, 75...$. Ce nombre est souvent désigné par la lettre grecque $\phi$.

Nous savons maintenant ce qu'est le nombre d'or et comment calculer sa valeur. Regardons désormais comment vérifier si deux longueurs données obéissent à cette divine proportion.

Suivez les instructions étapes par étapes pour déterminer si deux segments sont proportionnels au nombre d'or :

1. Trouvez la longueur du plus long segment et nommez-le « a ».
2. Trouvez la longueur du segment le plus court et nommez-le « b ».
3. Calculez a/b.
4. Si la proportion est (approximativement) égale à 1,618, vos segments sont en proportion dorée.

Vous pouvez également utiliser le calculateur du nombre d'or d'Omni pour effectuer cette opération. Bien que tout calculateur de ratio 🇺🇸 puisse vous aider, notre calculateur du nombre d'or traite spécifiquement de cette question. Vous ne trouverez pas meilleur outil !

Le calculateur du nombre d'or d'Omni est on ne peut plus intuitif et facile d'utilisation. Il comporte trois champs, correspondant aux trois longueurs qui apparaissent dans la formule du nombre d'or. Il vous suffit d'en entrer une pour que les deux autres soient calculées automatiquement. Formidable, non ?

Le rectangle d'or est un rectangle dont les côtés respectent le nombre d'or, c'est-à-dire que la proportion de sa longueur par rapport à sa largeur est de $1,\!618$. Ce rectangle est souvent utilisé dans l'art, car il est considéré comme le plus plaisant à regarder de tous les rectangles. Le calculateur du rectangle d'or 🇺🇸 est un moyen pratique de trouver les côtés d'un rectangle d'or au lieu de les calculer à la main.

Le nombre d'or a toujours eu une pertinence particulière en science et en art grâce à ses propriétés et à son apparence. En mathématiques :

• un rectangle d'or peut être divisé en deux rectangles d'or plus petits (il conserve ses proportions) ;
• le nombre d'or est étroitement lié au chiffre 5. Ce chiffre apparaît dans sa définition (φ = (1 + √5)/2) et dans le pentagone comme le ratio entre la diagonale et le côté.

Dans les arts, le nombre d'or est apparu plus récemment : Dalí, par exemple, a utilisé ce rapport dans bon nombre de ses œuvres.

De nombreuses sources historiques et contemporaines affirment que le nombre d'or est omniprésent dans la nature. En voici quelques exemples :

• le motif des feuilles lors de leur croissance ;
• les surfaces géométriques de certains légumes et coquillages ;
• les proportions des os de certains animaux.

Cependant, bien que nous ne puissions nier la présence de motifs géométriques dans la nature, nous ne pouvons pas non plus confirmer l'exactitude des proportions des exemples ci-dessus : certains présentent d'énormes variations, tandis que d'autres ne font qu'approcher le nombre d'or.