Calculateur de pente et dénivelé

Ce calculateur de pente et de dénivelé permet de déterminer la pente d'une surface terrestre de quatre manières différentes.

• En degrés, en mesurant l'angle entre la surface et le plan horizontal.
• En pourcentage, en divisant le dénivelé par la longueur de la pente.
• En tant que ratio, en divisant le dénivelé par la longueur de la pente et en le multipliant par 100.

Pour calculer la pente d'une droite, consultez notre calculateur de pente. Si vous voulez en savoir plus sur la détermination de la pente d'un terrain (ou du sol en général), poursuivez votre lecture.

La pente ou le degrée d'inclinaison mesure le niveau d'élévation d'un terrain. Elle peut être déterminée de différentes manières.

• En mesurant la différence d'altitude entre deux points de la zone.
• En calculant la moyenne des variations graduelles de la pente du terrain.
• En analysant les variations irrégulières de l'inclinaison du sol.

L'élévation du sol est généralement mesurée en fonction de son altitude par rapport au niveau de la mer.

Les géomètres et les ingénieurs sont chargés de mesurer et d'enregistrer ces inclinaisons à l'aide d'équipements et d'outils de surveillance.

Connaître la pente d'un terrain présente de nombreux avantages. Cela peut être essentiel pour des activités telles que la construction ou l'irrigation.

Voici quelques exemples concrets !

• La construction des routes : la pente d'une zone influence la conception des routes. Nous l'utilisons, par exemple, dans la formule de courbe verticale 🇺🇸. Un terrain très escarpé nécessite des routes en zigzag pour assurer la sécurité des usagers. Les ingénieurs peuvent également utiliser des techniques de déblaiement et de remblaiement pour réduire la pente d'un terrain.
• La construction de murs de soutènement : les murs de soutènement contiennent la terre face à l'érosion. Ils sont souvent construits contre des falaises pour prévenir les glissements de terrain. Si vous souhaitez en savoir plus sur ces murs en particulier, consultez notre calculateur de murs de soutènement.
• L'évaluation de la capacité du terrain à supporter une structure : la pente d'une zone peut affecter la stabilité d'une structure. Les structures construites sur un terrain en pente peuvent nécessiter des fondations plus solides.
• L'irrigation : la pente d'une zone peut influencer l'écoulement de l'eau. Les zones en pente peuvent être irriguées sans pompe, tandis que les zones planes nécessitent des pompes pour acheminer l'eau.
• Et bien plus encore. :)

La pente d'un terrain est calculée de la même manière que la pente d'une droite. Pour calculer la pente d'une droite, nous avons besoin des coordonnées de ses deux extrémités. La pente est le quotient de la différence des valeurs de y par la différence des valeurs de x. Sous forme d'équation, elle se présente comme suit :

Dans le monde mathématique, les changements de valeurs x et y ont des noms spécifiques. Le changement de valeurs de y est appelé « dénivelé » ou « distance verticale », il se déplace le long de l'axe des ordonnées. Le changement de valeurs de x est appelé « longueur » ou « distance horizontale » et se déplace le long de l'axe des abscisses. La pente peut alors s'écrire comme le quotient du dénivelé sur la longueur 🇺🇸 :

Nous pouvons également exprimer la pente en tant qu'angle. Pour cela, nous utilisons la trigonométrie pour calculer l'angle entre le plan horizontal et le plan incliné.

Nous appelons un angle qui monte à partir de la ligne horizontale un « angle d'élévation ». Un angle qui descend est un « angle de déclinaison ».

Pour calculer l'angle, nous utilisons la fonction arctan, qui est l'inverse de la fonction tangente. L'équation est la suivante :

Si vous n'avez pas de calculatrice avec la fonction trigonométrique arctan, vous pouvez utiliser notre calculateur de pente et dénivelé ci-dessus. Pour en savoir plus sur les autres fonctions trigonométriques essentielles, consultez notre calculateur de fonctions trigonométriques 🇺🇸.

En plus de la pente exprimée en quotient et en angles, nous pouvons également l'exprimer en pourcentage. Pour ce faire, il suffit de multiplier la valeur du quotient par 100. Une pente de 100 % signifie que la dénivelé de la pente est égale à sa longueur horizontale. Cette pente est considérée comme ni raide ni plate, mais plutôt comme une pente moyenne. Voici l'équation de la pente exprimée en pourcentage :

Notre calculateur de pente est équipé de toutes les équations nécessaires pour calculer la pente, la distance horizontale et l'angle d'élévation. Il suffit de saisir une valeur pour l'une des variables afin d'obtenir les valeurs des deux autres.

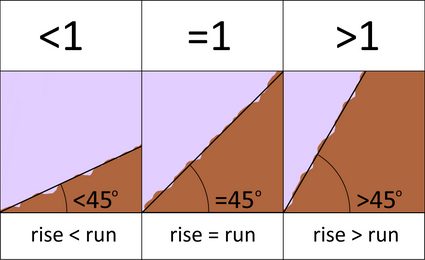
Les pentes sont faciles à comprendre. Une pente inférieure à 1 (pente du terrain < 1) signifie que le terrain est plat ou en pente douce. Une pente supérieure à 1 (pente du terrain > 1) signifie que le terrain est escarpé. En termes d'angle d'élévation, un angle supérieur à 45 degrés est considéré comme escarpé, tandis qu'un angle inférieur à 45 degrés est considéré comme plat.

Pour mesurer la longueur (distance horizontale), on peut utiliser un mètre ruban. Il est important de le tendre correctement pour obtenir une mesure précise. En effet, si le ruban n'est pas tendu, il s'affaissera sous l'effet de la gravité et la mesure sera plus élevée que la valeur réelle.

Pour mesurer le denivelé (la distance verticale), on peut utiliser un théodolite de géomètre associé à une mire. Le théodolite est un instrument optique qui permet de mesurer des angles et des distances. La mire est une règle graduée qui est fixée sur un trépied. En pointant le théodolite sur la mire, on obtient une lecture qui correspond à l'élévation entre la mire et le théodolite. Le théodolite peut également être utilisé pour mesurer des distances horizontales.

Outre le mètre ruban et le théodolite, il existe d'autres outils qui peuvent être utilisés pour mesurer la pente. L'inclinomètre est un instrument optique qui permet de mesurer l'angle d'élévation entre deux points. Il est comparable à un mini-télescope avec un rapporteur attaché sur le côté. Les smartphones, s'ils sont équipés de capteurs gyroscopiques, peuvent également être utilisés pour mesurer la pente. Il suffit de les poser sur la surface en question.

Pour représenter le relief d'un terrain, on peut tracer des courbes de niveau. Ces dernières forment ce qu'on appelle une carte topographique ; elle donne un aperçu de la nature du terrain d'une zone spécifique. L'exagération verticale permet de mettre en évidence les reliefs marqués, comme les montagnes ou les volcans.

Pour en savoir plus sur l'exagération verticale, consultez notre calculateur d'exagération verticale 🇺🇸.

Baldwin Street, en Nouvelle-Zélande, est connue pour sa pente vertigineuse de 0,35 . En effet, pour chaque mètre de dénivelé, il faut parcourir 2,86 mètres horizontalement. Cette rue de 350 mètres de long est donc un véritable défi à gravir !

Une pente de 0,35 correspond à un angle de :
angle = arctan(dénivelé/longueur) = arctan(1/2,86) = 19,27°.

La formule donne la pente définie comme un angle :
pente (angle) = arctan(dénivelé/longueur)
Le dénivelé correspond à la distance verticale et la longueur à la distance horizontale.
Pour calculer la pente en pourcentage, prenez l'argument de la fonction arctangente et multipliez-le par 100 :
pente (pourcentage) = dénivelé/longueur × 100

De manière plutôt contre-intuitive, une pente de 100 % correspond à un angle de 45°. Cependant, considérez que la pente est le résultat de l'équation :
pente = dénivelé/longueur
où :

• dénivelé – distance verticale
• longeur – distance horizontale

Une pente où chaque mètre horizontal correspond à un mètre vertical a une pente de 1, ce qui, multiplié par 100, donne 100 %.

Supposons que la route ait 12 mètres de dénivelé sur 200 mètres de long. La pente serait de 0,06. Pour calculer la pente d'une route avec :

• dénivelé = 12 m
• longueur = 200 m

1. Calculez le quotient du dénivelé sur la longueur :
   pente = dénivelé/longueur = 12/200 = 0,06
2. Si vous voulez connaître l'angle de la pente, entrez la valeur obtenue dans la fonction arctangente :
   pente (angle) = arctan(dénivelé/longueur) = arctan(12/200) = 3,43°
3. Si vous souhaitez connaître la pente en pourcentage, multipliez le rapport par 100 :
   pente (pourcentage) = 100 × dénivelé/longueur = 6 %