Calculadora de Tierra plana vs. redonda

¿Cuál es la mejor manera de aprender sobre el mundo? ¿Proponer una teoría y tratar de demostrarla con observaciones (ciencia)? ¿O simplemente inventar cosas (tonterías) e ignorar hechos evidentes? Aquí, en Omni, tendemos a pensar que la primera opción va bastante bien. Nos llevó a la Luna, ¿no? - Sí, claro que lo hizo

Para celebrar el Día Mundial de la Ciencia para la Paz y el Desarrollo, que se celebra cada 10 de noviembre, hemos creado una calculadora que te ayuda a luchar contra los disparates, las medias verdades y las tonterías, y a favor de la ciencia, la observación y la mente abierta.

La calculadora Tierra plana vs. redonda de Omni incluye experimentos que ayudan a demostrar que la Tierra es realmente redonda. No te preocupes; no tendrás que construir tu propio cohete para salir al espacio exterior y comprobarlo (ni calcular su impulso y cantidad de movimiento 🇺🇸 o su energía cinética).

Tenemos tres experimentos relativamente sencillos para que los pruebes:

• La doble puesta de Sol: Cambiando tu punto de vista sobre el suelo, puedes ver una puesta de Sol dos veces. Nuestra calculadora te dice cuánto verás de la segunda puesta de sol.

• Los objetos que desaparecen: Puedes ocultar objetos tras la curvatura de la Tierra cambiando la altura de tu punto de vista. Esta calculadora te mostrará la altura a la que puedes hacer desaparecer un objeto.

• Las sombras de un palo: Utilizando las longitudes de las sombras proyectadas por un palo en distintos lugares para calcular la circunferencia de la Tierra.

Antes de pasar a los experimentos, repasemos brevemente por qué la gente puede creer en una Tierra plana y el modelo del mundo que proponen.

Sorprendentemente, en el país más rico y tecnológicamente desarrollado del mundo, uno de cada seis habitantes no está seguro de que la Tierra sea redonda 🤔. Por supuesto, el país es EE. UU., y la creencia en una Tierra plana puede deberse a su cultura altamente individualista y a la desconfianza en la autoridad, las instituciones y los expertos.

Podemos pensar que esto se limita a los estadounidenses, que es donde se originó la encarnación moderna de este movimiento. Sin embargo, esta teoría "conspiranoica" va ganando adeptos por todo el mundo, e incluso entre todos los niveles de educación

Los terraplanistas parecen considerar el mundo por sí solos, sin referencia a los más de 2000 años de descubrimientos humanos. Bueno, ellos se lo pierden. También desconfían mucho de cualquier hecho que no hayan comprobado personalmente. ¿Alguien ha dicho de problemas de confianza?

Luego aceptan retos extraordinarios para demostrar que la Tierra es plana cuando hay cosas sencillas que podrían hacer para demostrar que la Tierra es redonda. He aquí algunos ejemplos:

• "Loco" Mike Hughes construyó sus propios cohetes propulsados por vapor para volar a una altura de 550 m (1800 pies) y fotografiar la falta de curvatura del desierto de Mojave. Por desgracia, para ver la curvatura de la Tierra hay que subir al menos a 11 000 m (35 000 pies). Lamentablemente, falleció en febrero de 2020 en un vuelo fallido de un cohete.
• La estrella de YouTube Logan Paul planeaba visitar la Antártida para encontrar el borde de una Tierra plana. Sin embargo, el viaje no tuvo lugar debido a la pandemia de COVID-19 y a la falta de instalaciones médicas para atender cualquier emergencia.
• El rapero B.o.B intentó financiar mediante micromecenazgo (crowdfunding) su propio lanzamiento de un satélite para buscar una Tierra plana. Solo consiguió recaudar 6883 $ de su objetivo de 1 millón de dólares. Bueno, no importa. Quizá podrían probar nuestros sencillos experimentos de bajo coste.

Este dibujo de Tom Fonder resume bastante bien a los partidarios de la Tierra plana.

En el modelo de la Tierra plana, el mundo es un disco (similar a los engranajes utilizados en los engranajes reductores de velocidad), con el polo norte en el centro. Alrededor del borde del disco está el hielo y la nieve del "polo sur". Este forma una barrera de hielo, presumiblemente para impedir que el agua de los océanos caiga del disco al espacio.

El grosor del disco de la Tierra plana no está claro. Sin embargo, la masa implicada debe ser mucho menor que la de una Tierra redonda, por lo que la Tierra no podría retener su atmósfera. Tal vez haya una cúpula transparente sobre la Tierra, que impide que los gases escapen.

En el modelo tradicional de Tierra plana, el sol está situado sobre el disco, dando vueltas en el cielo como el móvil de un bebé y a una distancia mucho más cercana. Eso no explica las puestas y salidas de sol. En aras de la cordura, imaginemos que el disco gira como una moneda respecto al sol. Eso nos devolvería al menos el amanecer y el atardecer (algo que hasta el más simple de los animales podría observar). Sin embargo, no habría zonas horarias, ya que la salida y la puesta del sol serían a la misma hora en todo el mundo.

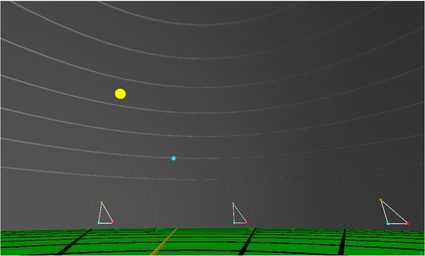
Ése es el principal problema del modelo de la Tierra plana. Está lleno de incoherencias y observaciones sin explicación. Por ejemplo, ¿por qué hace frío tanto en el centro como en el borde del disco?

Volvamos a una forma de pensar más científica e introduzcamos el primer experimento.

Este primer experimento puede ser muy sencillo de realizar. Muévete hacia arriba lo suficientemente rápido como para adelantarte a la sombra proyectada por el horizonte. ¡Entonces podrás ver parte de la puesta de sol dos veces! Si observas esto, entonces la Tierra es efectivamente redonda. Esta herramienta calculará qué parte de una segunda puesta de sol podrías ver y cuánto tiempo podrías hacer que durase una puesta de sol.

¿Qué verías si la Tierra fuera plana? No habría segunda puesta de sol 😭. Por muy alto o rápido que subieras desde la superficie de una Tierra plana, no volverías a ver el sol hasta el amanecer.

En una Tierra redonda, cuando el sol se pone, imagina que la sombra proyectada por el horizonte de la Tierra viene hacia ti y sube por tu cuerpo. Si consigues adelantarte a esta sombra moviéndote hacia arriba lo bastante rápido, podrás volver a ver la puesta de sol. Echemos un vistazo a las matemáticas.

Este documento nos da una ecuación que relaciona el tiempo con la altura de la sombra:

t = 8 × √h,

donde t es el tiempo que tarda la sombra en ascender una cierta altura h. Podemos relacionar h con la diferencia entre dos alturas y t con el tiempo que tarda en desplazarse hacia arriba. Como no podemos desplazarnos instantáneamente de la altura inferior a la superior, debemos tener en cuenta el tiempo de desplazamiento. Por último, para hallar la cantidad de una segunda puesta de sol que podemos volver a ver, necesitamos conocer la duración de la puesta de sol. Entonces tenemos esta ecuación para el porcentaje de la segunda puesta de sol que volverás a observar:

Porcentaje de puesta de sol dos = 100 × (1 - ((Duración de la puesta de sol - t - Tiempo de viaje) / Duración de la puesta de sol))

Hay algunas formas de volver a ver el sol justo después de que se haya puesto, en distintos grados. La calculadora Tierra plana vs. Tierra redonda de Omni te dirá qué parte de la segunda puesta de sol podrás observar. Veamos tres ideas que se nos han ocurrido.

1. Échate al suelo, ponte de pie

Esta idea es la más sencilla en cuanto a equipamiento. Sólo necesitas un lugar donde puedas ver la puesta de sol en el mar o en un terreno muy llano (como un desierto). Un bonito cielo despejado también ayudará. Lo único que tienes que hacer es observar la puesta de sol echado en el suelo. En cuanto ya no puedas ver nada del sol, levántate lo más rápido que puedas. Deberías poder volver a ver un poquito de la parte superior del Sol.

A continuación te explicamos cómo utilizar la calculadora para calcular exactamente cuánto.

1. Selecciona la ubicación más cercana a ti o introduce manualmente la duración de la puesta de Sol en el lugar donde te encuentres.
2. Introduce la altura inicial más baja del nivel de tus ojos. En este caso, cuando estés en el suelo. Normalmente en torno a unos 20 cm (8 pulgadas).
3. Introduce el tiempo que tardarás en alcanzar la altura superior. Calculamos que alrededor de medio segundo, pero puedes cronometrarte para comprobarlo.
4. Introduce la altura final de tus ojos cuando estés de pie. Puedes medirla restando a tu altura la distancia entre la parte superior de tu cabeza y tus ojos.
5. Verás cómo se fija el porcentaje del sol que podrás volver a ver. ¿Quieres ver más? Prueba a cambiar los valores en la calculadora o prueba las variaciones más avanzadas del experimento que te contamos a continuación.

Con este método deberías poder ver alrededor del 5 % de la segunda puesta de sol.

2. Elevación rápida de un rascacielos

Para ver más de la segunda puesta de sol, tendrás que subir más alto y más rápido para adelantarte a la sombra del horizonte. Un rascacielos con ascensores muy rápidos es una buena opción. Este fenómeno se ha observado en el hotel Burj Khalifa de Dubai.

Para introducir los valores correctos para este rascacielos, escoger "Sky scrapper lift - hotel Burj Khalifa" (en castellano sería Ascensor de rascacielos - hotel Burj Khalifa) entre las opciones predeterminadas. Si quieres probarlo en otro edificio, ajusta los valores adecuadamente.

Deberías poder volver a ver un enorme 88 % de la puesta de sol, y así casi duplicar la duración. Si eres un amante de las puestas de sol, esto es exactamente lo que debes hacer.

3. Dron con cámara

Otra idea es utilizar un dron de buena calidad que tenga capacidad para emitir una cámara en directo. Hemos encontrado algún dron que puede alcanzar 1000 m (3300 pies) en 200 segundos. Si seleccionas "Drone" en la lista de ideas, verás que podrías volver a ver aproximadamente un tercio de la puesta de sol con este método.

Comprueba lo rápido y alto que puede llegar tu dron y ajusta los valores de la calculadora en consecuencia.

En este experimento, ocultaremos parte de un objeto tras la curvatura de la Tierra. Tendrás que encontrar una masa de agua en la que la orilla más alejada esté al menos a dos kilómetros de distancia (1.25 millas), y tiene que ser un día despejado, con el mar en calma y sin viento.

Además, para evitar el efecto de espejismo (refracción de la luz), haz el experimento por la mañana, cuando hace fresco. También por eso no es recomendable utilizar un desierto: el efecto espejismo hará que no puedas ver con suficiente claridad los objetos de la orilla lejana.

En este vídeo de YouTube, hicieron desaparecer un camión situado a 7 km (4 millas) en la orilla más alejada de un lago acercando la cámara al suelo.

Alternativamente, un parque eólico marino también es una buena opción, como demuestra esta fotografía:

Fíjate que cuanto más lejos está un molino de viento, más se oculta. De eso trata este experimento: de calcular cuánto de un objeto lejano puedes ocultar tras la curvatura de la Tierra.

En este experimento, empezaremos desde un punto de vista alto y luego bajaremos a un punto de vista bajo para ocultar un objeto lejano. Hallaremos matemáticamente cuánto se oculta en los puntos de vista alto y bajo y calcularemos la diferencia.

Para calcular la altura ocultada, primero necesitamos conocer la distancia al horizonte. Esto viene dado por esta ecuación

a = √[(r + h)² - r²]

donde:

• a es la distancia al horizonte,
• h es el nivel del punto de vista sobre el suelo, y
• r es el radio de la Tierra, igual a 6.371 km (o 3.959 millas).

A continuación, introducimos el resultado en una segunda ecuación que calcula cuánto del objeto (que se encuentra a una distancia d) se oculta, x, si se ve desde una altura cero:

x = √(a² - 2ad + d² + r²) - r

La diferencia entre los dos valores de x (punto de vista alto y el punto de vista bajo) es la altura del objeto que podemos hacer desaparecer cambiando nuestro punto de vista.

Vale, has encontrado un lugar adecuado, como un lago con la orilla a unos kilómetros. Para ver cualquier objeto en la orilla lejana, necesitarás unos buenos prismáticos. O alternativamente, una cámara de vídeo con un objetivo con gran zoom. Eso también te permitiría grabar el experimento, como en el vídeo anterior.

Para obtener una visión estable a través de los prismáticos o la cámara, se recomienda montarlos en un trípode. Utilizar un trípode también te permitirá medir las dos alturas con precisión.

A continuación te explicamos cómo utilizar la calculadora para averiguar el tamaño del objeto que podrías hacer desaparecer tras la curvatura de la Tierra.

1. Mide la distancia hasta la orilla más alejada del lago. Para ello, puedes utilizar un mapa de papel o la función de medición de Google Maps. Introduce la distancia en la variable "Distancia al objeto" de la calculadora.
2. Mide la altura de tus ojos sobre el suelo cuando estás de pie o de tu cámara cuando esté en la posición alta. Introduce esta altura en el siguiente campo de la calculadora.
3. Haz lo mismo cuando estés echado en el suelo o tu cámara esté en la posición de altura baja. Para maximizar el efecto, intenta situarte lo más bajo posible con respecto al nivel del agua.
4. Entonces verás que se calcula la altura de un objeto que está oculto por la curvatura de la Tierra. Si te parece demasiado pequeño para verlo, intenta aumentar tu altura alta y disminuir tu altura baja.

Si la Tierra fuera plana, no verías ninguna diferencia en los objetos del otro lado del lago, independientemente de la altura a la que los veas.

Este experimento no sólo demuestra que la Tierra es redonda, sino que también permite calcular su circunferencia. Esto es precisamente lo que hizo el matemático griego Eratóstenes en Alejandría, hacia el 240 a.C.. Sabía que en Asuán, a unos 800 km al sur, había un pozo en cuyo fondo llegaba la luz del sol al mediodía del solsticio de verano. Al mismo tiempo, midió la sombra proyectada por un palo en Alejandría.

Suponiendo que la Tierra es redonda y el sol está muy lejos, y utilizando las matemáticas que veremos más adelante, llegó a la conclusión de que la circunferencia de la Tierra era unas 50 veces la distancia entre Alejandría y Asuán. Es decir, erró por menos de un 10 % respecto a la respuesta correcta. Un resultado fantástico para un experimento tan sencillo realizado hace más de 2000 años.

Observando el triángulo formado por el palo y la sombra, podemos utilizar la función trigonométrica arcotangente para calcular el ángulo entre el palo y el rayo de luz solar, utilizando la ecuación:

θ = arctan(Longitud de la sombra / Altura del palo)

Repetimos lo mismo para las dos ubicaciones. ¿Cómo se relacionan estos dos ángulos con la circunferencia de la Tierra? La figura siguiente nos ayudará a responder a esta pregunta.

Utilizando un poco de geometría, podemos demostrar que el ángulo α entre las líneas que pasan por los lugares A y B, y el centro de la Tierra, es la diferencia de los ángulos de sombra de los palos:

α = θ₂ - θ₁

Ahora conocemos la longitud del arco (distancia a lo largo de la superficie de la Tierra) entre A y B, y el ángulo α. Esto nos permite simplemente escalar la distancia a la circunferencia completa de la Tierra, utilizando la ecuación:

Circunferencia terrestre = (Distancia A→B) × (360° / α)

Es importante señalar que la distancia de A a B debe ser la distancia si sólo pudieras viajar en dirección norte o sur (la distancia norte-sur). Necesitamos esta distancia porque
únicamente cuando te desplazas hacia el norte la sombra proyectada por el palo se alarga.

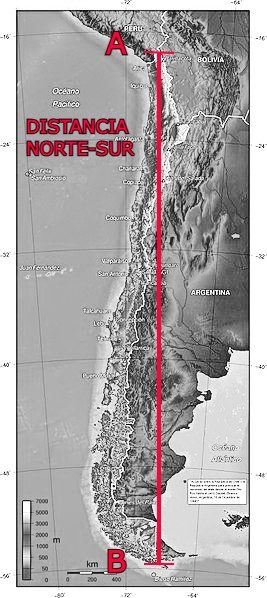
En el caso general, suponiendo que el punto A está al norte del punto B, traza en un mapa una línea hacia el sur desde el punto A. Luego traza una línea hacia el este desde el punto B. La distancia norte-sur es la longitud desde el punto A hasta donde se cruzan las dos líneas que has trazado.

Para un país como Chile, los puntos A y B están prácticamente uno al norte del otro, por lo que la distancia norte-sur es prácticamente la misma que la distancia geométrica.

Hay dos formas principales de intentar este experimento. Puedes viajar una distancia considerable hacia el norte o el sur (más de 160 km, cuanto más lejos, mejor) o asociarte con alguien que viva lejos para que te ayude.

Empecemos por la opción de viajar. Lo mejor es intentarlo alrededor del día más corto o más largo del año, ya que la duración del día es relativamente estable. Eso reducirá los errores en el ángulo de sombra medido en los dos lugares. Aquí tienes las instrucciones paso a paso:

1. Mide la longitud del palo. Tendrás que introducirla en el cuadro de entrada superior de la calculadora. Si parte del palo está enterrado, incluye solo la longitud por encima del suelo.
2. Mide la longitud de la sombra en el lugar A a la hora local del mediodía. Lo mejor es que sea un día soleado o con pocas nubes para poder verla bien. Introduce la longitud de la sombra en la calculadora y se calculará el ángulo de la sombra.
3. Viaja al lugar B y haz lo mismo que en el paso 2.
4. Utilizando un mapa, mide la distancia norte-sur entre los dos lugares e introduce esta cifra en la calculadora (consulta las instrucciones anteriores).
5. Recibirás entonces la respuesta a tu estimación medida de la circunferencia de la Tierra y lo cerca que te has quedado de la respuesta real.

Si tienes un amigo en otro lugar que te ayude, ¡mejor aún! El experimento será más exacto si realizas ambas mediciones el mismo día del año y a la misma hora solar. En este caso, los pasos son básicamente los mismos. Asegúrate de que los dos palos tienen la misma longitud y de que mides la sombra al mediodía, hora local, del mismo día. Esta opción es mucho más fácil y puede hacerse en cualquier día soleado del año.

Por poner un ejemplo, volvamos a Chile. Supongamos que tenemos un amigo que viaja al punto más al norte de Chile (A en el mapa anterior), mientras que nosotros nos desplazamos al punto más al sur (B). La distancia norte-sur, como hemos dicho antes, es de 4270 km. Vamos a decir que ambos llevamos un palo de 1 m de alto y que la sombras que producen son de 0.27 m en el punto A (norte de Chile), y de 1.3 m en el punto B (sur de Chile). Esto significa que nuestro amigo verá un ángulo de sombra de 15.11º en el punto A, mientras que en el punto B nosotros tendremos un ángulo de sombra de 52.43º.

Si introducimos estos valores en la calculadora obtendremos un resultado de 41 188 km. Es decir, dentro del 3 % de la circunferencia real medida entre los polos de 40 008 km. ¡Lo hemos hecho mejor de lo que lo hizo Eratóstenes!

Imaginemos por un momento que los de la Tierra plana tienen razón (lol). ¿Cómo quedaría el ejemplo anterior en un modelo de Tierra plana?

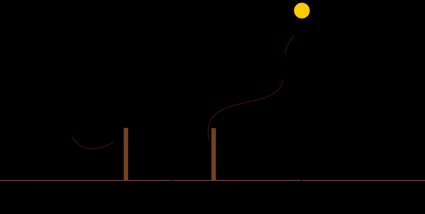
En un modelo de Tierra plana, los palos seguirán proyectando una sombra de longitudes diferentes. Sin embargo, al hacer un poco de trigonometría se llega a un resultado extraño. Refiriéndonos al diagrama anterior y aplicando las mismas fórmulas, podemos decir que

d = h × |tan θ₂ - tan θ₁|

Utilizando los ángulos 15° y 52°, y 4270 km para d, vemos que la distancia al sol h es

h = 4270 / |0.27 - 1.28| = 2445.5 km

Esto parece demasiado cercano. Sin embargo, el modelo de la tierra plana puede decir que el sol es mucho más pequeño de lo que la ciencia ha concluido.

Ahora podemos calcular las otras dos distancias al sol desde los dos lugares:

R₁ = h / cos θ₁ = 2445.5 / cos(15°) = 2531.8 km

R₂ = h / cos θ₂ = 2445.5 / cos(52°) = 3972.1 km

Este resultado significa que al viajar 4270 km hacia el sur, el sol debería haberse reducido hasta un 63 % de su tamaño original. En realidad, como puedes comprobar por ti mismo, el sol no parece hacerse más pequeño a medida que viajas hacia el sur.

Por tanto, podemos concluir que el modelo de la Tierra plana es erróneo, ya que no concuerda con la observación. Esa es la propiedad crucial de cualquier modelo científico. Debe concordar con los resultados experimentales.

La noción de que la Tierra es esférica es bastante antigua. En la antigua Grecia, los científicos y filósofos ya eran conscientes de este hecho en el siglo V a.C.

Incluso en siglos posteriores, el modelo esférico fue aceptado en más lugares y sólo marginalmente cuestionado fuera de los motivos puramente mitológicos: el aparente resurgimiento y relevancia de esta teoría en los tiempos modernos es puramente una consecuencia del cambio en nuestros métodos de comunicación.

Para calcular la circunferencia de la Tierra mediante sombras:

1. Pide a un amigo que viva en una latitud diferente que realice los mismos pasos que tú.
2. Planta verticalmente en el suelo un palo de longitud conocida.
3. Mide el ángulo entre el palo y los rayos del sol a una hora concreta del día local.
4. Utiliza la fórmula
   θ = arctan(Longitud de la sombra / Altura del palo).
5. Utiliza ahora esta fórmula para la circunferencia de la Tierra
   Circunferencia terrestre = Distancia × (360° / α),
   donde:
   • Distancia es la distancia norte-sur entre los palos; y
   • α es la diferencia entre los ángulos calculada antes.

Para ver la curvatura de la Tierra, debes estar a una altitud de unos 10.5 km. Esta es aproximadamente la altitud de crucero de un avión de pasajeros. Sin embargo, para verlo correctamente, necesitas un horizonte completamente despejado (sin nubes) y un campo de visión de al menos 60 grados. Estas dos condiciones rara vez se cumplen desde las ventanillas de tu avión, pero puedes intentarlo.

Además, ¡fíjate en que la curvatura no es visible ni siquiera desde la cima del monte Everest!

Para demostrar que la Tierra es redonda, ¡ve a la playa! Si tienes delante una extensión de mar lo suficientemente larga, puedes esperar simplemente a que un barco se acerque a la costa. Primero verás aparecer su parte superior por encima del horizonte, seguida lentamente por el resto del barco.
Como la Tierra es redonda, su curvatura cubre parte del barco. La parte cubierta se hace más pequeña a medida que el barco se acerca a ti.

Ahora, ¡lo difícil es convencer a los escépticos de que ésta es una respuesta definitiva!